摘 要 : 根据问题已知条件构造表达式是求解数学题的一种重要方法.本文以举例的方式介绍 几种常见构造表达式解题的类型，以说明构造表达式在解题中的重要作用.

　　关键词 : 构造,表达式,解答,数学题

 　　构造表达式是解数学题的一种重要方式.在 一些数学题中，构造表达式可以达到事半功倍的 效果.然而，构造表达式的方法没有固定的模式， 要求解题者能根据题目已知条件联想到所学知 识进行构造，其中蕴含转化与化归、类 比等重要 的数学思想.本文将举例谈谈几种常见的构造表达式的类型.

　　1 构造齐次等式

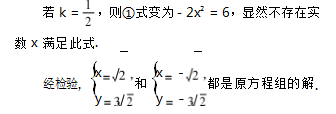
　　评注 原方程组中两个方程除常数项外都是齐 二次的，因此考虑构造齐一次等式 y = kx，再将其代 入原方程组化简达到减少未知数个数的目的，进而 容易求解原问题.

　　例 2 已知实数 x 和 y 满足 x2 + 2y2 -xy -1 = 0.求f = x2 + 2y2 的取值范围.

　　评注 将目标表达式变形代入已知等式，可以 由该等式构造齐次等式，如此便于减少未知数个数， 从而利用一元二次方程有解的条件求解目标式的取值范围.

　　2 构造多项式

　　例 3 证明 : ab + bc + ca> -1.其中 a，b，c 都是 绝对值小于 1 的实数.
       令f( x) = ( b + c) x + bc，容易发现这是一 个一元且至多一次多项式.因为| b | <1.| c | <1.

　　评注 此证明将 a，b，c 三个量中的一个看成未知 数，从而构造了一个一元且至多一次多项式，利用该多项式在区间上的单调性，容易证明原命题.
       例 4 已知 a，b，c，d 是给定的互不相等的实

      因为 a，b，c，d 互不相等且f ( -a) = f ( -b) = f( -c) =f( -d) = -1.所以f( x) = -1.

      这就说明原命题成立.

　　评注 根据所要求证的内容构造 一 元且 不 超过三次的多项式，一方面容易发现它有四个不 同实根，而另一方面不超过三次的非常值多项式 最多有三个实根，因此容易知道该多项式是一个常值多项式.

　　3 构造含参表达式

　　评注 此证明中，通过构造含参表达式，将所证不 等式的左边转化为只与所构造参数有关的表达，可以 看到此时只需利用实数的平方非负这个基本事实就可以轻松证明原式.

　　4 构造对偶式

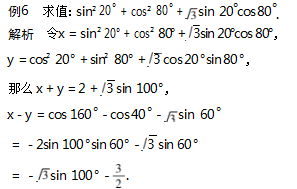
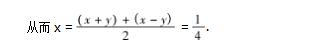
　　评注 构造互余三角对偶式后，可以充分利用 三角函数的运算性质将原问题进行转化与化简，从 而容易求得原式的值.

　　评注 根据函数f ( x ) 所满足等式的特点，在该等式中用1/x代替 x 可以构造对偶式，再用消元法即可得到函数f ( x ) 的表达式.

　　5 构造递推式

　　评注 根据已知构造熟知的等比递推式，容 易得出新数列的表达式，此后根据新数列的特点 使用累加法即可求得数列{an }的通项公式.

　　6 构造复数表达式

　　评注 构造复数表达式后，利用复数的运算性 质可以得到有助于解题的方程，再研究该方程解的 性质，即可得到原问题的解.

　　上文从构造齐次等式、构造多项式、构造含参表 达式、构造对偶式、构造递推式以及构造复数表达式 六个方面，举例介绍了构造表达式解题的方法.当 然，构造表达式解题的类型不只有上述六类.

　　构造表达式解题不仅可以帮助学生建立数学知 识间的联系，还能拓宽学生的数学思维，培养学生的 创新能力.在教学中，教师应当引导学生学会使用此 方法解题.

参考文献 :

　　[1]邹海斌.在构造中体验数学创造之美[J].数学 教学通讯，2022 (15) : 57-58 .