【摘要】初中数学教学要以发展学生数学核心素养为导向，突出数学本质，应关注内容主线之间的关联以及同一个内容主线中重要知识点之间的关联。注重知识背后的数学思想、方法的贯通，注重形、数之间的结合，引导学生进行学习内容逻辑线索的梳理。本篇借助圆中的基础图形，引导学生进行一题多解，一解多题。进一步强化在数学实践活动中综合运用数学知识的能力。

　　【关键词】核心素养,圆,直角三角形

　　初中几何学习“始于点，而终于圆”。圆象征圆满、完美，也有自在的含义。初中几何最后一章为圆的学习，实际上是新旧知识间的融合，是总结，也是一种包容。如何让我们在圆的学习中自在起来呢？简单的以圆中的直角三角形为切入点，略谈一二。

　　在圆中构造直角三角形是一种重要的解题技能，圆中一些题目，添线构造直角三角形，可使隐含条件显露，将分散条件集中，从而帮助学生迅速打开思路，化归到解直角三角形。而在圆中构造基础图形——直角三角形，初中阶段最常见的是垂径定理和直径所对的圆周角为直角这两种方法。

　　同样的直角三角形，垂径定理的应用侧重于求边与边之间的关系，而直径所对的圆周角更侧重于角度有关的计算。但在圆的综合应用中，这两者的关系并没有分得那么细，更取决于学生当时的第一反应。而学生的反应与判断则来源于平常的学习和探究。如何提高学生的数学思想及解题能力？这就要求教师平时要帮助学生进行归纳总结，借助圆中的基础图形，引导学生进行一题多解，一解多题，进一步自我提升，择优解题。

　　例1：已知：A、B、C三点不在同一直线上，

　　（1）若点A、B、C均在半径为R的⊙O上，如图1-1，当∠A=45。，R=1时，求∠BOC的度数和BC的长；如图1-2，当∠A为锐角时，求证：sinA=

　　（2）若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动，如图1-3，当∠MAN=60。，BC=2时，分别作BP⊥AN，CP⊥AM，交点为P，试探索在整个滑动过程中，P、A两点间的距离是否保持不变？

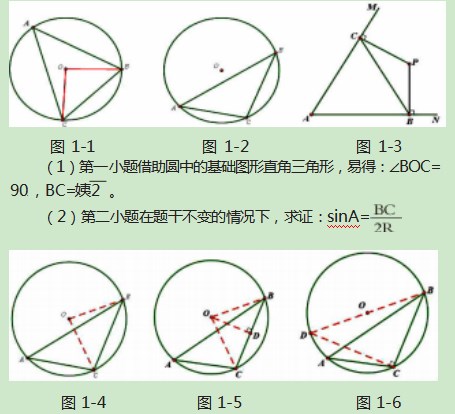
　　在第一小题的引导下，学生通常会借鉴图1-1，连结OB、OC，去寻找解题思路（如图1-4）。但也可能产生困惑，出现∠A的两倍，倍角公式不会用，如何延续自己的想法呢？继续引导学生去观察图形，发现△OBC为等腰三角形，让学生会借助垂径定理，过点O作OD⊥BC于D（如图1-5）。通过同弧所对的圆周角是圆心角的一半及直角三角形、垂径定理的知识解题。把知识的应用又往前推进了一步。

　　若能够引导学生重新读题，结论sinA=，其中2R为直径，如果过BO作直径BD，连结CD，构造一个（如图1-6），让BC，2R都出现在里面。结论显而易得。把知识的应用又提升了一步。

　　（3）第三小题则把圆中的基础图形——直角三角形的整个知识的应用推到了一个高潮，首先通过直角三角形中直角所对的斜边为外接圆的直径，证明点A、B、P、C都在⊙K上(如图1-7)，再利用sin60。=，得出AP=(定值)。

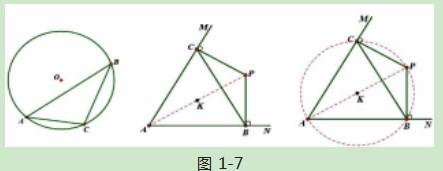
　　如上的想法和做法有些时候是教师的一厢情愿，不同的学生还会通过各种不同的方法来解答，此时教师应该给学生充分的时间讨论，引导他们一题多解，训练发散思维。然后让学生对比作法，从中选择最佳的解题方法(如图1-6)。

　　一题多解，不仅能对知识进行迁移，同时也进一步强化在数学实践活动中综合运用数学知识的能力。

　　此时跟进相应的例题，让他们做出多题一解，更进一步训练收敛思维。让他们收放自如。

　　例2:已知：在⊙O中，弦AB=2，CD=1，AD⊥BD。

　　（1）如图2-1，直线AD，BC相交于点E，求∠E的度数；

　　（2）如图2-2如果点C，D在⊙O上运动，且保持弦CD的长度不变，那么，直线AD，BC相交所成锐角的大小是否改变？试就以下三种情况进行探究，①如图Ⅰ,弦AB与弦CD交于点F；②如图Ⅱ,弦AB与弦CD不相交；③如图Ⅲ,点C与点B重合。

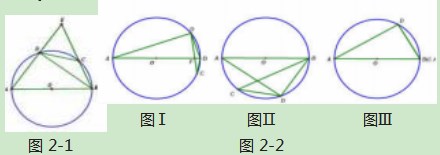
　　解一道题目，不外乎是强化条件，分析结论。第一小题中，题目给定的条件很简约，但从中“我”能得到哪些结论，此时可以让学生罗列出来，并由此引申出各种解题思路。

　　在已知条件当中，给定两条弦长，其中一条是直径，自然而然的想到了构造基本图形——直角三角形，直径为斜边，另一弦为直角边，所求的角的大小则为其中的一个三角函数值所对应的角度。此时借助例1中的图1-6的解题方法。帮助学生把所有的条件都引入到，一网打尽，答案呼之欲出。

　　对于第2小题，参考第1小题的方法，让学生去发现圆上的弦CD在动，实际是位置的变化，但形状并没有变化，等式关系依然存在。最终2个问题呈现在我们面前的实际上是这样一种情况（图2-3）。从例1延续到例2，实际上是一解多题的呈现。

　　一题多解，可以开阔学生思路、发散学生思维，使学生学会多角度分析和解决问题；而多解归一，可以加深学生对数学原理、通性通法的认识，提高解题技巧与能力。这些想法，做法要得以实施，需要我们在日常教学中，依托基础知识，逐步推进，让学生“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”。

　　[1]《福建省初中学科教学与考试指导意见》

　　[2]《数学例题》

　　[3]《泉州中考真题》

　　[4]《山东中考真题》