摘要:错题讲评课是一种重要的课型，教师在讲评时，不能满足于一题一讲，也不应止步于形式上的一题多解，一题多变，而应该抓住机会，适时引导，还主体于学生，鼓励他们独立思考，类比细究，拓展延伸，归纳感悟．

　　关键词:错题讲评;思维品质;细究感悟

　　如何在数学课堂教学中落实数学核心素养的培养，一直是一线教师的重要课题．错题讲评课是一种重要的课型，它不仅是知识掌握的一个必要环节，可以帮助学生找到思维盲区，纠正错误，拓展思维，开发创造性等，也可以帮助老师弥补新授课中的教学不足，同时，也能很好地提升逻辑推理、数学运算、分析问题、归纳概括等能力．但我们经常听到教师会抱怨，讲评过的错题，为何学生又错?自认为讲清楚了，其实学生还没有听懂;自认为简单的，学生觉得难;自己滔滔不绝40分钟，口干舌燥，学生却掌握甚少;学生课堂听懂了，课下又忘了．．．．．．很是无奈．不能调动学生积极性，不能让学生思维处于活跃状态下的错题讲评课，仅有老师一人滔滔不绝的分析错因，讲解正确思路，哪怕老师讲得口干舌燥，学生也未必买账，效果必然是低下的．那如何能让讲评课收到好的效果呢?现笔者结合自己的教学实践，从四个方面对错题讲评方式展开探究与思考．

　　1由此及彼，类比讲评

　　类比方法是一种重要的数学思维方法，它可以使知识条理化，把复杂的问题简单化，它能帮助学生融会贯通所学的知识，提高学生分析问题、解决问题的能力，同时能较好地培养学生的逻辑思维能力和创新能力．

　　题1已知△ABC为等边三角形，AB=2．设点P，Q满足=λ，=(1－λ)，λ∈R，若·=－，则λ=;

　　题2在矩形ABCD中，AB=，BC=2，E为AE·BF的值是．

　　评注题1为上完新授课2．4．1平面向量数量积的物理背景及其含义后作业本中的题目，由于当时仅讲了数量积的定义，所以在作业讲评时仅讲了“基底法”，如何选基底，如何运算．题2为上完新授课2．4．2平面向量数量积的坐标表示、模、夹角(二)后作业本中的题目，由于此课时是数量积的坐标表示，所以“坐标法”必然是要讲评的．但作为一名教师，如果仅仅会当下学啥就只讲啥，那就太片面了，不利于学生数学知识的系统提升．笔者在讲评课时，遇到同类、相似问题就很喜欢让学生往前翻翻作业本，比如讲到题2时，等学生领会“坐标法”后，笔者就让学生翻到作业本57页，让学生比对这两道题，不说多余的话，就给学生充足的时间去比对，去思考，去动手演算，去感悟．结果学生自己就能发现原来这两道题是同一种题，题1也可以利用正三角形图形本身的对称性建系，从而用“坐标法”解决，—→—→基底，从而用“基底法”解决．代数法(基底法，坐标法)是解决向量问题的重要方法，通过这样的类比讲评，重点突出，从老师引导学生类比，到学生自主类比，从而感悟总结，学生思路更清晰，理解更到位，知识更成系统，学生的思维能力也得到了很好的提升．

　　题3若函数f(x)=log2(x2+2ax－a)的定义域为R，则实数a的取值范围为;

　　题4若函数f(x)=log2(x2+2ax－a)的值域为R，则实数a的取值范围为．

　　评注题3与题4学生常常将“定义域为R、值域为R”搞混，只知道时而△＜0，时而△≥0，但是弄不清楚何时用哪个．如果老师讲评时，能将这种“形同而质不同”的题目放在一起进行类比讲解，必能激发学生的好奇心、探究欲望，变被动思维为主动自觉思维，从而引发学生仔细掂量，认真剖析，真正从问题本质去挖掘，得到的学习效果也就自然不一样了．题3是定义域为R，即不管x取何值，对应的整个真数都要大于0，即转化为x2+2ax－a＞0恒成立，所以△＜0．题4是值域为R，也就是要确保整个真数能取遍一切正数，一个值也不能落下，那么只能y=x2+2ax－a这个二次函数与x轴有交点了，所以△≥0．学生做错题目不可怕，可怕的是学生仅停留在简单的记忆模仿上，时间一长必然忘记．通过类比讲评，让学生悟透问题本质，才能从根源上消除再次犯错的隐患，类比讲评很好地培养了学生的差异性思维，提升了学生的类比分析能力，对提升数学素养大有裨益!

　　2借题发挥，拓展讲评

　　拓展讲评就是俗话说的在原有题目的基础上，增加新的东西，延展加深．老师在讲评作业本、试卷中的错题时，不要“就题讲题”，我们可以借题发挥，针对错题进行一题细研、一题多法、一题多变，它实现的不仅仅是表面上数量的变化，而是质量的变化．

　　拓展讲评可以拓展学生思维的广度，挖掘思维的深度，提升思维的高度．

　　题5已知向量a=(2，λ)，b=(3，－4)，且a·b的夹角为钝角，则λ的取值范围为．

　　题6已知角A=60°，a=3，求△ABC的周长的取值范围．

　　题7已知数列{an}，a1=1，an+1=3an+2，求数列的通项．

　　评注题5不少学生都做出答案λ＞来了，少数学生错的题目是不是就不用讲评了呢?非也!要知道有时学生答案对，思维未必就严密．笔者抛出变式:如果a=(－2，λ)，b=(3，－4)，答案又如何?果然很多同学只考虑数量积小于0，而忽略cosθ＞－1这个条件，出来错误答案λ＞－．笔者不动声色，在黑板上写下答案为λ＞－且λ≠，大家觉得诧异，勾起了好奇心，开始探究讨论，发现其实应该满足－1＜cosθ＜0，钝角不包括180°．由于原题中的向量a与b不会出现反向共线的情况，所以同学们漏掉一头还是出来了正确答案，学生思维中有不严谨性，老师要有这种预判能力，借助题目，慢慢细研．

　　题6是三角函数章节检测中某题的第二问，少数做对的学生普遍是由余弦定理得b2+c2－9=2bccosA=bc，进而使用基本不等式得到3＜b+c≤6，从而得到周长的范围．笔者在讲评时表扬了这种做法，简洁、计算量少，同时询问学生还没有别的思路，引导学生处理范围问题实际上就是处理值域问题，在三角函数区块处理值域我们最擅长的是什么法?学生立马回答合一变形为Asin(ωx+φ)+B模式，继续问此处谁是变量?显然是“角”，继续追问那周长是个边的问题，如何转化为角呢?在老师的引导下，学生自然知道可以使用正弦定理化边为角，从而得到b+c=(sinB+sinC)=[sinB+sin(A+B)]=6sin(B+)，问题也就迎刃而解了．

　　笔者问道“两种解法，感受如何?”学生异口同声“我们的解法快，计算量少．”笔者笑笑，肯定了学生，同时在黑板上写下“求2b－c”，学生立马觉悟基本不等式不管用了，以角为自变量的函数思想来依然可以处理此题，将它化为2b－c=6sin(B－)即求得范围，所以函数思想才是通性通法．笔者讲评试卷中的错题时，借题发挥，适时引导，让学生体会基本不等式和函数思想两种解法各自的优势所在，让学生亲历由“误”到“悟”的过程，实现悟一题通一类，让学生跳出题海，减轻负担!

　　题7为初学等比数列后的常见题目，在递推式的两边同时加1，得到an+1+1=3an+3=3(an+1)，构造出一个公比为3，首项为2的新等比数列{an+1}问题就迎刃而解了．但是如果老师仅仅是就题讲题，泛泛而谈，尤其是后期复习阶段，学生拥有一定的构造能力时，更不能单讲题7，老师应抓住此题，借题发挥，进行一题多变，将递推式变为变式1:an+1=3an+3n+1，变式2:an+1=2an+3n+1，让学生观察变式1，变式2与原题的不一样之处，结合学生已经会处理an+1=Aan+B(B为常数)型的题目了，引导学生如何转化不熟悉题目为熟悉题目?学生很容易联想到将3n+1位置变成常数就可以了，如何变为常数呢?只需两边同除3n+1即可，后面就一切顺理成章了．借题发挥没有结束，继续抛出变式3:an+1=3an－4n+2，又将如何呢?似乎不能变成常数来处理了，老师可以再次引导学生观察原题an+1=Aan+B(B为常数)型，我们是如何找到一个新的等比数列的?本质是把常数B拆分了，使得左右两边刚好an+1+C=A(an+C)，从而构成了新的等比数列．在此引导下，学生就会把握本质，将“－4n+2”进行拆分，找到an+1－2(n+1)=3(an－2n)，从而构造出新等比数列．借题发挥结束了吗?没有!变式2、变式3是否也可以直接拆分3n+1呢?事实上变式3可以拆分为an+1－3·3n+1=2(an－3·3n)，这样就直接找到等比数列{an－3·3n}，而不需要变为an+1=Aan+B(B为常数)型再去构造等比了．

　　3多题一法，归纳讲评

　　在学生的错题中存在一些“形不同而质同”的好题，它可以事半功倍地提升学生的思维品质、数学素养，但是光有好题不够，需要有一双发现它的眼睛，如果针对这些“形不同而质同”的题目，老师只是给一个正确解法，不去深究，那么题目依然是散的，学生听完后领悟不深刻，下次出错率依然会很高．

　　思路就终止了．题10是2020学年第一学期杭州市高三统测的填空题16题，学生会把条件平方得到a 2+b 2－a b=1，也会把目标变为求a 2+a b的最大值，但是怎么求，没想法了．为何题8学生耳熟能详，看到都会做，但是面对题9，题10，却没了方向?问题是不是出现在我们老师讲错题时仅仅做到“就题讲题”，而没有很好地去引导学生总结归纳呢?所以学生看到的都是分散的，不系统的．如果我们老师平时讲评这些“形不同而质同”的错题时，能多多引导学生去观察、感悟、就不难归纳出这里是多题一法，就会发现他们本质是一样的，都是处理二元问题，那么只需要同“齐化切”一样，化二元问题为一元问题即可.

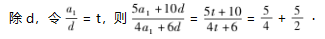
　　函数的最值问题变为一元函数的最值问题．我们常说要针对学生的最近发展区实施教学，既然题8是学生耳熟能详的，那为何不引导学生去悟透呢?三角、数列、向量看似三个不一样的知识区块，虽形不同但质同，老师需要实施多题一法，引导学生归纳总结出通性通法，通过有限道题的探究去领悟解决无限道题的数学机智，真正提升学生分析问题，解决问题的能力．

　　4角色互换，学生讲评

　　富兰克林曾说:告诉我，我会忘记，教给我，我可能记住，让我参与，我才能学会．错题讲评的目的是对学生所学的知识进行查缺补漏，必须充分调动学生的积极性，让学生直接参与到课堂中来是最有效的方式．故可以采用学生讲评和教师讲评结合的方式，与教师讲评相比，学生的思维相通，通过学生间的语言交流也许更能让那些不会的同学豁然开朗，学生讲评可以使学生在讲评中相互启发，共同提高．

　　题10平面向量a，b的夹角为60°，且a－b=1，则a·(a+2b)的最大值为;

　　再看题10，笔者讲评时为了突出多题一法，所以是引导学生将二元问题转化为一元问题来处理的．讲评完后，立马有学生举手示意了，他们有不一样的想法．这时老师千万不要因为讲评整张卷子时间紧张，而错失一次让学生展示、成长的好机会，就该让他们畅所欲言，各抒己见．

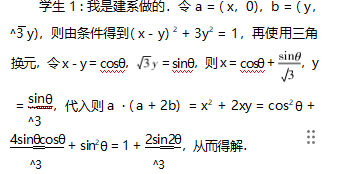
　　学生4:利用求根公式用a表示b，我也想到了，但是后面看着函数关系式太烦，不知道怎么求最值就放弃了，当时忘记用导数了．

　　师:不错!虽然计算看起来繁琐，但是把握住了函数思想的本质，条件给了二元a，b的关系式，必能用其中一个表示另一个，从而实现二元变一元．同时也提醒了大家，求最值的法宝导数．

　　错题讲评教学在数学教学中有着重要的地位，教师在讲评时，不能满足于一题一讲，也不应止步于形式上的一题多解，一题多变，而应该抓住机会，适时引导，还主体于学生，鼓励他们独立思考，类比细究，拓展延伸，归纳感悟．教师不只要交给学生数学知识、思想方法，更要教会学生如何思考，探寻从无到有，从有到优的思路，如此才能提升、优化学生的思维品质，这样的讲评课才是有效的．

　　参考文献:

　　[1]唐俊涛．解题细节促能力课堂教学育素养[J]．中学教研(数学)，2018(11):8－11．

　　[2]刘成龙，蒋红珠，叶薇．对一个二元最值问题的探究[J]．中学教研(数学)，2018(10):19－23．

　　[3]武瑞雪．摭谈数学试卷讲评课的“四要”“四不要”[J]．中学数学教学，2017(5):19－22．