摘要:同构法在近几年的模考中频繁出现，把等式或不等式变形为两个形式上一样的函数，利用函数的单调性转化为比较大小、解恒成立或者求最值等问题，同构法在使用时，考验“眼力”，面对复杂的结构，仔细观察灵活变形，使式子两侧的结构一致，从而构造函数．

　　关键词:同构法;导数;双变量型;指对跨阶型

　　用导数比较大小、解不等式，其关键在于利用题目条件构造辅助函数，把比较大小、解不等式问题转化为先利用导数研究函数的单调性，进而根据单调性比较大小或解不等式．

　　1双变量型

　　含有同等地位的两个变量x1，x2的等式或不等式，同构后使等式或不等式两侧具有一致的结构，便于构造函数解决问题．常见的同构类型有:

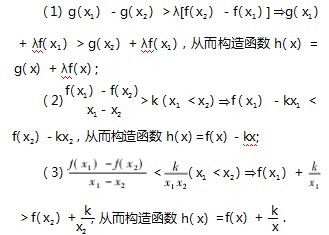
　　评注例1中出现的双变量问题是同构法中较为典型的情况，思路明确，针对上述类型的不等式，分离变量，构造函数，利用函数单调性，解不等式．

　　2指对跨阶型

　　解决指对混合不等式时，常规的方法计算复杂，则将不等式变形为f[g(x)]＞f[h(x)]的结构，f(x)即为外层函数，其单调性易于研究．常见变形方式:

　　2．2先凑再变形

　　若式子无法直接进行变形同构，往往需要凑常数、凑参数或凑变量，如两边同乘以x，同加上x等，再用上述方式变形．常见的变形有:

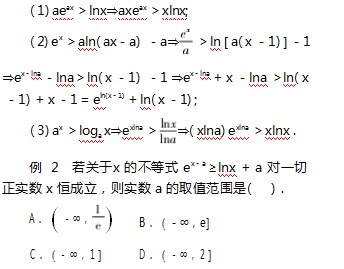
　　分析不等式两侧都加上x，即能出现同构法中的“和差型”．由不等式的结构判断，通过将不等式变形为ex－a+x－a≥lnx+x，符合同构法中的指对同阶模型．

　　解析将条件不等式两侧都加上x得到ex－a+x－a≥lnx+x．

　　1．所以g(x)在(1，+∞)上单调递增，在(0，1)上单调递减．

　　故g(x)min=g(1)=1，故a≤1．故选C．

　　评注不等式或函数中指对数结构都存在时，仔细观察结构特征，可优先考虑放缩或同构，化繁为简，降低单调性判断的难度．故要对常见不等关系的结论及上述的常见变形方法牢记于心，能够熟练变形，构造相应函数．

　　3同构放缩或同构换元共存型

　　有些更复杂的指对不等式，利用常见的变形方法先进行同构变形再换元，使构造的函数较为简单，或者不等式本身的结构不特殊，可以先结合常用不等结论放缩．常见的放缩模型:

　　评注第(2)问进行指对变形，换元简化函数，同构法让复杂的函数式在指对结构上呈现“一致性”，再换元，大大降低了函数研究的难度，但这类问题，方法不唯一，也可利用其他方法，比如不等式证明问题，直接构造函数求最值，或者变形为f(x)＞g(x)的结构，比较最值．

　参考文献:

　　[1]巨小鹏．几道高考题背后的破解秘密———同构[J]．数理化解题研究，2022(01):55－58．