摘要:本文对一道江苏地区高三期中测试中的向量系数和为定值问题进行了解法探究，推广得到了椭圆中的一般性结论，并将相关结果引申到了双曲线和抛物线中，最后变换视角进行了拓展探究．

　　关键词:系数和;定值;探究;椭圆;双曲线

　　1试题呈现

　　2解法探究

　　视角1(设线法)设出直线l的方程并与椭圆方程联立，通过向量关系将λ1，λ2用两根表示，再借助韦达定理求解．

　　解法1(正设直线)显然直线l的斜率存在，F(1，0)，设A(x1，y1)，B(x2，y2)，直线l的方程为y=k(x－1)，与椭圆方程联立消去y，得

　　解法2(反设直线)易知F(1，0)．当直线l的斜率不为零时，设A(x1，y1)，B(x2，y2)，直线l的方程为x=my+1(m≠0)．

　　视角2(代点法)直接设出A，B，P三点的坐标，通过向量关系解出A，B两点的坐标并代入椭圆方程，再借助丰达定理求解．
　　解法3易知F(1，0)．设A(x1，y1)，B(x2，y2)，P(0，n)，则PA=(x1，y1－n)，AF=(1－x1，－y1)．

　　视角3(参数法)借助椭圆参数方程设出A，B两点的坐标，通过向量关系得到参数关系，再利用和差化积与积化和差公式求解．

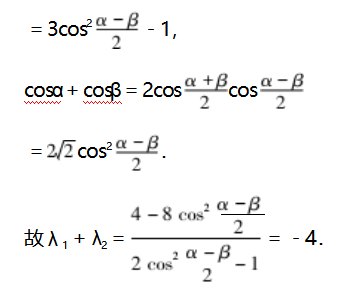
　　3推广引申

　　将试题第(2)问进行一般化推广得到:

　　4对偶拓展

　　受文[1]启发，将命题2和命题4中点E的位置改为y轴上，分别得到:

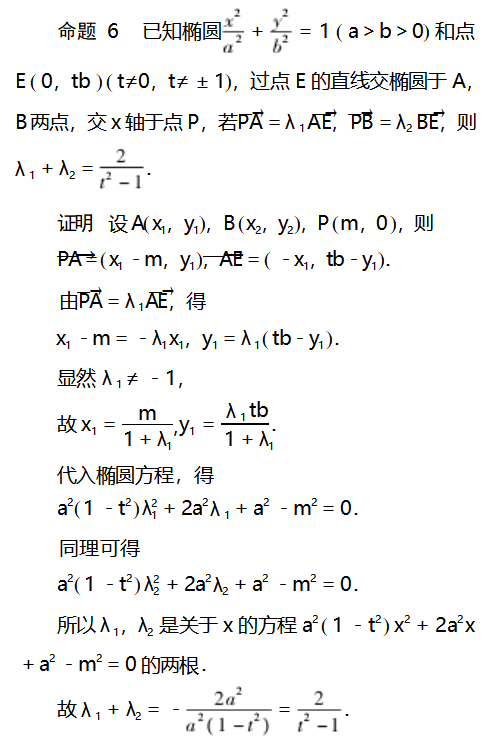
　　5方法运用

　　我们对命题的证明采用了前面的解法3进行，借助同构方程思想使得问题的解决过程简洁明了，运算量小．下面给出两个变式练习题，供参考．

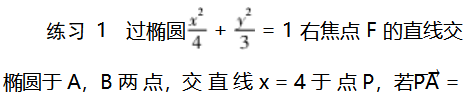
　　参考文献:

　　[1]高继浩．探究一道斜率之比为定值的联考试题[J]．数学通讯，2021(19):36－37．

　　[2]高继浩．揭开“蝴蝶”的面纱———对一道2021年重庆市预赛题的探究[J]．中学数学教学，2021(06):30－32．