摘要:本文从2020年全国Ⅰ卷理科21题的一道圆锥曲线试题出发，透过题目具体数量关系探究其内在联系，经过深入分析论证，形成具有普遍意义的结论，并尝试加以证明．

　　关键词:圆锥曲线;定点;定直线

　　1问题的提出

　　(1)求E的方程;

　　(2)证明:直线CD过定点．

　　笔者在对该题探究中发现，问题可推广到圆锥曲线的椭圆与双曲线的一般情形，有如下结论:

　　2结论的证明

　　2．1结论1的证明

　　证明依题意有A(－a，0)，B(a，0)．
　　如图1，设直线x=ka与x轴交于点M．

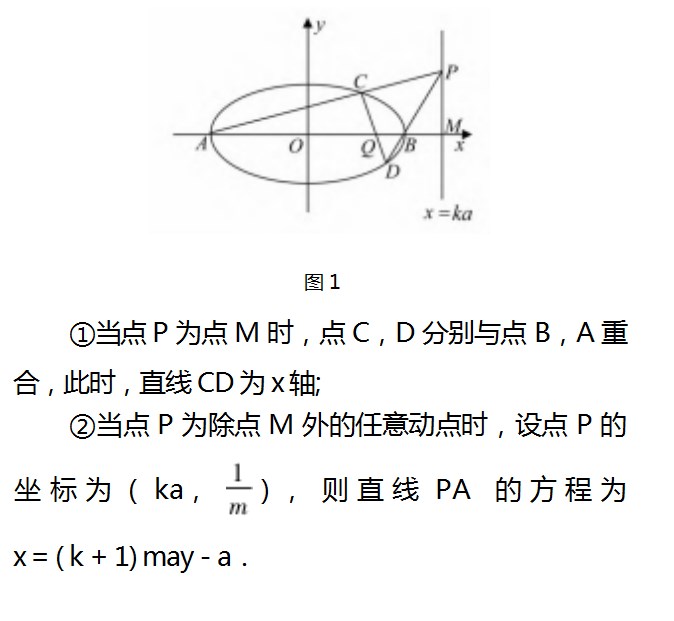
　　注(1)圆锥曲线中的椭圆为封闭曲线，直线PA，PB与椭圆一定存在两个交点，结合图象可知，当0＜k＜1时，直线CD不可能垂直于x轴;当k＞1时，存在条件(k2－1)m2 b2=1，使得直线CD垂直于x轴;

　　(2)根据椭圆具有的对称性质，该结论在k＜0且k≠－1时仍然成立，故将结论1可推广到k≠0，k≠±1的任意常数结论都成立;

　　(3)上述2020年全国Ⅰ卷理科21题为结论1在a=3，b=1，k=2的特殊情形．

　　2．2结论2的证明

　　证明依题意有A(－a，0)，B(a，0)．
　　如图2，设直线x=ka与x轴交于点M．

　　(2)根据双曲线具有的对称性质，该结论在k＜0且k≠－1时，仍然成立，故亦可将结论2推广到k≠0，k≠±1的任意常数结论都成立．

　　3结论的拓展

　　结论3，4与结论1，2的条件与结论对调，易于证明结论3，4，本文不再赘述．

　　参考文献:

　　[1]邓启龙．2020年全国Ⅰ卷理科数学第20题的探究与推广[J]．理科考试研究，2021，28(03):2－6．

　　[2]杨伟达．2020年全国Ⅰ卷理科解析几何第20题的剖析与探究[J]．数理化解题研究，2021(31):33－34．