摘 要：为了帮助学生对初中数学复杂问题进行简化探究和有效解答，文章研究了“设而不求”解题技巧在初中 数学教学中的具体应用。首先概述“设而不求”内涵与价值，其次以人教版初中数学教材为参考，结合大量例题 说明“设而不求”具体的应用方向和解题过程，最后简要总结全文内容，以期为初中数学教师提供有益参考。

　　关键词：初中数学;解题技巧;“设而不求”

　　在初中数学教学中，一部分复杂题目不能直接通 过设未知数求解，而是要应用“设而不求”解题技巧，这 要求教师指导学生掌握“设而不求”解题技巧，培养 学生解决问题的多元思维。初中数学教师应主动理 解“设而不求”解题技巧内涵与价值，找准典型例题，引 导学生探究应用情境与方法。

　　一、“设而不求”的内涵与价值

　　“设而不求”是初中数学问题解决方法之一，指 的是在解决某些复杂问题时设定一些未知数，然后将 未知数视为已知数，根据题目本身各已知条件，通过 整体消元简化问题解决过程，在降低解题难度的基础 上提高解题的准确性。对于初中数学解题教学来说， “设而不求”是极为重要的一种方法，使学生掌握初 中数学“设而不求”解题技巧，不仅可全面提高他们 在代数方程、函数、几何图形等方面的学习质量，还 能使他们在中考时游刃有余地处理复杂题、压轴题。 初中数学教学离不开“设而不求”的解题技巧。教师 应对此加以重视，结合典型例题指导学生。

　　二、“设而不求”在初中数学教学中的应用

　　(一)化简运算问题

　　化简运算属于初中数学基础知识，如有理数化简 运算、整式化简运算等。虽然相较于方程、函数、空 间几何等知识点，化简运算问题较为简单，但也有一 部分初中数学化简计算问题具有一定复杂性，学生不 能通过常规方式找到解题思路和答案，此时就需要运 用“设而不求”解题技巧 [1]。

　　例如，在人教版数学八年级(下册)“二次根式的 加减”教学中，有如下问题：

　　先化简，再求值：根号6+根号11+根号6-根号11

　　问题包含两个根式，无形中增加了化简与运算难 度，但若细心观察不难发现，被开方数有理数部分相 同，无理数部分互为相反数。根据这一发现，可推测 解题过程或许与以下两公式有关：

　　平方差公式：(a+b)(a-b) =a2-b2

　　完全平方公式：(a±b)2 =a2+2ab+b2

　　应用“设而不求”解题技巧，借助新的未知数表 示算式中复杂的根式，学生可巧妙地将复杂根式化简 求值问题转化为“开平方”问题，进而通过平方差公 式与完全平方公式的创新运用实现准确解题。

　　(二)代数方程问题

　　1. 三元一次方程组“设而不求”解题技巧三元一次方程组为人教版数学七年级(下册)“二 元一次方程组”拓展延伸内容，也是初中“方程组”问 题的重要内容。常规解题思路为通过“代入”或“加 减”进行消元，将“解三元一次方程组”转化为“解二元一次方程组”，再转化为“解一元一次方程”，计 算较为烦琐。教师可以向学生讲解相关“设而不求”解 题技巧，巧解三元一次方程组问题 [2]。

　　例如：有麻料、棉料、毛料三种布料，若购 3 匹 麻料，7 匹棉料，1 匹毛料，共需 315 元;若购 4 匹麻料， 10 匹棉料，1 匹毛料，共需 420 元。现在购麻料、棉料、 毛料各 1 匹，共需多少元?

　　结合题意，可设麻料、棉料、毛料的价格分别为 x、 y 、z 元，列出下面方程组：

　　3x+7y+z=315 … …(1)

　　4x+10y+z=420 … …(2)

　　解方程，联立(1)(2)：(1)×3-(2)×2.可得 x+y+z=150.求出原问题正确解。

　　对比传统解法“一一求出未知数取值，然后将它 们相加，求得问题最终解”，此解法先设未知数，然后 将“x+y+z”视为一个整体，有效地简化了计算过程。 教师还可基于此问题变式，鼓励学生进行变式练习，巩 固对应“设而不求”解题技巧。

　　2. 分式方程“设而不求”解题技巧

　　分式方程为人教版数学八年级(上册)的重要内 容，主要目标是使学生正确地理解分式方程概念，通 过求解分式方程解决实际问题。但是， 基于“分式”复 杂性，分式方程实际求解过程通常较为烦琐， 易使学 生出现计算失误。这就要求教师在分式方程问题中， 同 样向学生传授“设而不求”的解题技巧。

　　(三)函数问题

　　人教版初中数学函数问题包括一次函数、二次函 数、反比例函数、锐角三角函数，贯穿八九年级。其 中，二次函数图像面积问题、反比例函数面积问题等， 均可应用“设而不求”解题技巧求解 [3]。

　　例如，在 人教 版 教学 在 人教 版 数学 九年 级(下 册)“反比例函数”教学中，有下面这一道关于面积 的题：

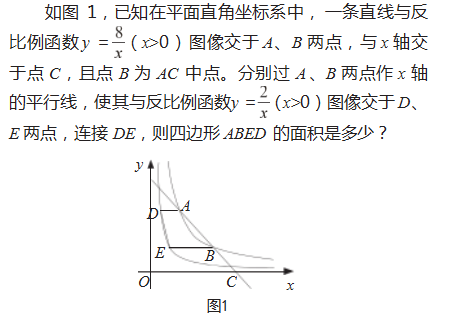
　　(四)几何问题

　　初中数学几何求值问题包括“求角度”“求长 度”等，但由于很多时候题干没有给出足够的角度与 长度信息，解题思路并不清晰，需要引入未知数。学 生可以通过未知数逐步表示出解题所需角度或长度， 然后根据未知数在整个几何图形中的等量关系，顺利 求出待求角度或长度 [4]。

　　例如，在人教版数学八年级(上册)“三角形”教 学中，有以下问题：

　　已知 RtΔABD 中(如图 2)，∠ ABD = 90°, C、E 分别为线段 AD 上的两点，满足∠ BAC =∠ BCA，BE 将∠CBD 平分为∠CBE 与∠DBE，求∠AEB 的度数。

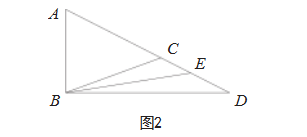
　　这是典型的几何图形“求角度”问题。基于问题 逆推， 若想求出∠AEB 的度 数， 需要用到 ∠ CBE、 ∠CBD、∠ABD、∠ACB 等多个角度，但是对于这些角， 题干都没有给出明确的度数。因此，可结合已知角与 图形信息，将它分别设为不同未知数，解题过程如下：

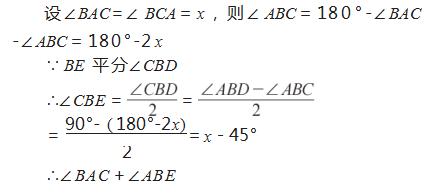
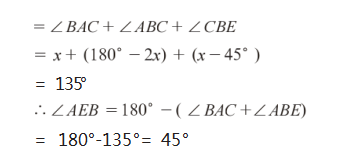
　　通过“设而不求”解题技巧，设∠BAC 与∠BCA 为未知数 x，从而在未知角与已知角间顺利建立联系， 最后基于三角形内角和等量关系抵消未知数，求出待 求角度，整体解题过程更加简洁、高效。

　　(五)实际应用问题

　　“设而不求”解题技巧还可以应用在初中数学实 际应用问题的解决中 [5]。广义上，初中数学问题可分 为“数学问题”与“实际问题”两部分，上述例题可 统称为“数学问题”。“实际问题”通常与现实生活息 息相关，意在使学生避免“书本化”“应试化”的学习， 将所学知识与技能运用在实际生活中。然而在一些实 际问题中，学生同样会遇到不能借助已知条件解题的 复杂情况，需要迁移运用“设而不求”解题技巧。

　　例如，在人教版数学八年级(下册)“一次函数” 教学中，有以下问题：

　　明珠社区组织了一次团购活动，联系了两家旅行 社，由 2 名导游带队，旅行票原价相同。 A 旅行社购 票优惠活动为“1 名导游不优惠，其他导游与居民 7 折 优惠”。B 旅行社购票优惠活动为“全体导游与居民 7.5 折优惠”。假设当参与团购的居民人数是多少时，两家 旅行社收费相同?

      为了简化计算，可将两家旅行社旅行票原价设为 a，参与团购居民人数设为 x，则两家旅行社收费情况 分别为：

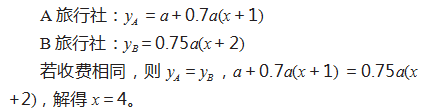
　　若基于常规列方程思路求解，由于不确定旅行票 原价，很难顺利解题。而融合一次函数与“设而不求” 解题技巧，通过设未知数在 A 、B 旅行社收费之间建 立函数关系，便可轻松解出题中所提问题。

　　三、结束语

　　言而总之，“设而不求”解题技巧是初中数学非常重要的解题思想与方法之一。教师应通过合理引导帮 助学生掌握“设而不求”解题技巧，使他们能够在面 对复杂问题时，最大限度地简化解题过程，提高效率与准确率。初中数学教学应大力完善“设而不求”解 题技巧教学，以此提高学科整体教学质量。

参考文献

　　[1] 陈兴菊 .“设而不求”思想在数学解题中的运用[J] . 初中数学教与学,2022(23):21-23 .

　　[2] 李斌.设而不求解题技巧在初中数学解题中的应用[J] . 数理天地(初中版),2022(17):69-71 .

　　[3] 张琳 .“设而不求”巧解初中数学竞赛题[J].初中数学教与学,2022(9):45-46 .

　　[4] 胡敬婷.例谈“设而不求”技巧在初中数学解题中 的应用[J].新课程导学,2022(9):60-62 .

　　[5] 丁鹏儒 . “设而不求”解题技巧在初中数学解题中 的应用[J].数学大世界,2021(6):79 .