摘要：为从能量耗散角度研究不同井下工况对球面-锥面特殊螺纹接头密封面处密封性的影响，借助 ABAQUS 有限元软件建立了球 面-锥面特殊螺纹接头密封面的模型-球面-平面接触模型，得出了不同切向位移载荷、不同压力和不同摩擦因数下的载荷-位移迟 滞曲线的变化规律; 利用密封接触强度理论评价特殊螺纹接头的密封性能。结果表明： 摩擦因数越大， 可承受的宏观滑移载荷越 大; 随着载荷的增大， 密封面呈现刚度软化现象。部分滑移状态和完全滑移状态下，接触区域的能量耗散值都随着切向位移载荷、 压力和摩擦因数的增大而增大， 说明密封性能有所降低。由密封强度理论得当压力处于 15~40 MPa 时， 密封面均满足密封要求; 随着压力的增大， 密封接触强度增大， 密封性能也随之提高。研究结果可为井下复杂工况条件下提高球面-锥面特殊螺纹接头密封 性能提供参考。

　　关键词：特殊螺纹接头; 能量耗散;球面-锥面; 密封性能; 有限元

　　Analysis of Energy Dissipation and Sealing Performance of Spherical-cone Premium Connection

　　Qin Yanbin ，Li Juncheng ，Yu Yang ，Cao Yinping ，Dou Yihua

　　(Mechanical Engineering College, Xi ’an Shiyou University, Xi ’an 710065. China)

　　Abstract: In order to study the effect of different downhole working conditions on the sealing surface of spherical-cone premium connection from the angle of energy dissipation, a sphere-plane contact model is established for the sealing surface of spherical-cone premium connection by using ABAQUS finite element software, and the changing law of load-displacement hysteresis curve under different tangential displacement load, different pressure and different friction coefficient is obtained. The area change of the hysteresis curve reflects the law of energy dissipation. The sealing performance of premium connection are evaluated by using the sealing contact strength theory. The results show that the larger the friction coefficient is, the larger the macroslip load by the load-displacement hysteresis backbone curve; with the increase of load, the sealing surface showed stiffness softening phenomenon. The energy dissipation value of the contact area increases with the increase of tangential displacement load, pressure and friction coefficient in both partial and complete slip states, indicating that the sealing performance decreases. According to the sealing strength theory, the sealing surface meets the sealing requirements when the pressure is 15~40 MPa; with the increase of pressure, the sealing contact strength increases and the sealing performance also improves. The study results provides reference value for improving sealing performance of spherical-cone premium connection under complex working conditions.

　　Key words: premium connection; energy dissipation; spherical-cone; sealing performance; finite element

　　引言

　　由于现代勘探技术的发展， 大量高温高压井被大规 模开发， 井下工况愈发恶劣， 对油管接头的密封性能带 来了更大的挑战[1]。为了满足高温高压井的要求， 具有 良好密封性能的特殊螺纹接头被广泛应用。与 API 螺纹 相比， 特殊螺纹接头主要增加了金属对金属主密封面和 扭矩台肩辅助密封的密封结构来满足各种复杂工况下的 使用性能[2]。特殊螺纹接头的类型繁多， 由于接头设计 思路的不同， 使得主密封结构的类型繁多， 目前常用的 主密封类型主要包括锥面-锥面密封、球面-锥面密封、 柱面-柱面密封等[3]。当特殊螺纹接头受压力和切向载荷作用时， 特殊螺纹接头密封面处带有摩擦的微观滑动引 起能量耗散，从而对特殊螺纹接头的密封性能产生影响。

　　目前鲜有对于特殊螺纹接头在能量耗散方面的研究， 但在螺栓连接方面的研究较多。孙德林[4]通过建立三维 螺栓搭接连接的有限元模型， 对不同预紧力和载荷作用 下的螺栓连接的能量损耗规律进行了研究。 Shamoto 等[5] 建立了连接螺栓的扭转接触模型， 然后利用有限元结果 线性组合的迭代计算以及扭矩平衡方程， 得出了接触界 面上的黏着和滑移区域， 并对所提出的模型进行了试验 验证。张颖等[6]基于特殊螺纹接头能量耗散模型， 研究 了密封面处不同锥度对特殊螺纹接头能量耗散的影响规律。 Xiao 等[7]利用基于双线性摩擦的微滑模型， 着重考 虑了 4 种不同幂函数指数的压力分布形式对搭接连接能 量耗散的影响规律。窦益华等[8]首先推导出特殊螺纹密 封面处一维连续体微滑理论模型， 然后建立密封面搭接 有限元模型， 分析了界面特性、压力和锥度对密封面处 能量耗散的影响规律。

　　特殊螺纹接头作为油管的连接结构， 在复杂的载荷 工况下常发生密封失效， 甚至由此引发安全事故。曹银 萍等[9]通过建立球面-锥面和锥面-锥面 2 种特殊螺纹接头 有限元模型， 研究了气密封检测对特殊螺纹油管接头密 封性能的影响。练章华等[10]利用数值模拟和新的气密封 评价方法， 对 2 种特殊螺纹接头在上扣、轴向拉伸、轴 向压缩工况下的连接强度以及复合载荷工况下的密封性 能进行了研究。刘祥康等[11]建立了某特殊螺纹的三维有 限元模型， 得到了油管发生屈曲对特殊螺纹性能的影响 规律。 Murtatisu 等[12]采用物理测试和数据模拟方法， 通 过密封面密封性能与接触压力的函数关系， 计算推导出 密封强度和临界密封强度的计算公式， 只有当密封强度 大于临界密封强度时， 特殊螺纹接头才具有较好的密封 能力。Xie 等[13]依据实际经验对临界密封强度计算公式进 行了优化， 提出了在高温高压井中， 可采用优化后的公 式计算特殊螺纹油套管接头密封临界强度。 ZENG 等[14] 对连接器 VX 钢圈的密封特性进行分析时， 得出应该优 先选择密封强度作为密封性能评价指标。 Yu[15]利用密封 强度理论，分析了不同载荷下特殊螺纹接头的密封性能。

　　在此背景下， 本文首先考虑 2 个接触面的微滑运动， 分析能量耗散机理;其次，建立球面-锥面特殊螺纹接头 主密封面的简化模型-球面-平面接触的有限元模型， 分 析不同切向位移载荷 s、压力p 和摩擦因数对载荷-位移迟 滞曲线的影响规律;最后，利用密封强度理论，分析不同 压力下特殊螺纹接头的密封性能。研究结果可为复杂工况 条件下提高球面-锥面特殊螺纹接头密封性能提供参考。

　　1 能量耗散机理分析

　　特殊螺纹接头在井下服役期间受到循环载荷、内压 与外压的影响， 其密封面处容易受到切向载荷和法向载 荷的影响， 在密封面处发生微动滑移， 从而产生能量耗 散。微观滑动会引起能量耗散。在分析与微滑相关的能 量耗散时， 首先要确定滑移发生的区域。 2 个接触体的 运动可以分为以下 2 个阶段。

　　( 1) 部分滑移状态： 当切向载荷较小时， 接触区域 局部出现滑移， 其他区域依旧保持黏着状态， 其载荷- 位移迟滞曲线如图 1(a)所示。

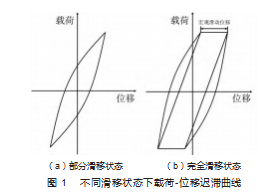
　　(2) 完全滑移状态： 当切向载荷足够大时， 整个接 触区域都产生了滑动， 且有宏观滑移的产生， 其载荷- 位移迟滞曲线如图 1(b)所示[14]。

　　通过对比部分滑移状态和完全滑移状态的载荷-位 移迟滞曲线示意图可以得出， 完全滑移状态时的载荷- 位移迟滞曲线存在很明显的宏观滑移， 因此可以通过有 无宏观滑移来区分 2 种滑移状态。

　　2 球面-平面接触有限元模型建立

　　2.1 接触模型建立

　　API 螺纹是通过螺纹啮合和螺纹脂来实现密封， 但 随着高温高压等极端恶劣工况的出现， 高温对螺纹脂 影响较大以及高压会导致啮合后存在泄漏通道。而特 殊螺纹接头的出现则较好地解决了这一问题， 与 API 螺纹不同的是， 特殊螺纹接头不再依靠螺纹啮合实现 密封， 主要通过增加金属对金属的主密封和扭矩台肩 辅助密封结构。

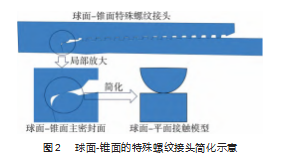
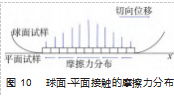
　　为研究球面-锥面特殊螺纹接头主密封面处的能量 耗散规律， 将球面-锥面的主密封结构简化为球面-平面 的二维接触问题， 如图 2 所示。在有限元软件 ABAQUS 中建立球面 -平面接触有限元模型， 网格划分如图 3 所 示。模型设定球面半径为 6 mm， 矩形的长宽分别为 12、 6 mm。材料属性μ=0.3 ，E=200 GPa[16]。对有限元模型的 接触面进行接触属性设置， 切向行为摩擦公式设置为拉 格朗日乘子(standard)， 摩擦因数为 0.02. 法向行为设 置为硬接触[17]。设置相互作用时，采用主面-从面的设置 定义 2 个接触面， 球面的下表面为主面， 平面的上表面 为从面，这种设置便于提取接触区域的节点数据。

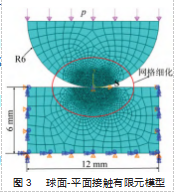
　　模型所施加的载荷和边界条件： 在球面的顶面施加 均布的压力p， 使两接触面能够紧密接触; 同时， 在球 面的底面中心施加交变的切向位移载荷 s ，使两试件能够 沿接触区域切向方向产生相对位置变化， 从而引起 2 个物体间的能量耗散。平 面两侧约束水平方向位 移， 底部约束竖直方向 位移。为保证上下 2 个部 分接触计算结果的收敛 性， 有限元模型采用四 结点双线性平面应力四 边形单元(CPS4R)[18]， 并且对球面-平面模型的 接触区域进行网格细化处理， 细化网格大小为 0.02.

　　2.2 接触模型加载过程

　　在接触分析中， 如果在第 1 步中就把全部载荷施加到模型上， 有可能分析无法收敛， 故在第 1 步施加一个从 0开始增加的压力p， 让接触关系平稳地建立起来， 从第 2 步再开始施加切向位移载荷 s。

　　二维球面-平面接触有限元模型的加载过程如图 4 所示。

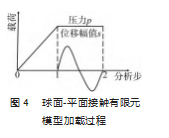
　　加载过程主要分为以下 2 个步骤：

　　( 1)第 1 个加载过程的时间步长为 1.在球顶面中心 施加恒定的压力p;

　　(2)第 2 个加载过程的时间步长也为 1. 到第二部分 之后，压力p 保持恒定，并施加周期性的切向位移载荷s。

　　2.3 接触模型验证

　　为验证所建立模型的有效性， 在进行分析前， 使用 经典的Hertz 接触理论验证模型的正确性，对接触压力的解析解与有限元解进行比较。接触压力分布的解析式[19]为：

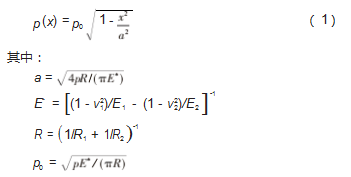
　　式中：p 为压力， MPa;x 为接触区域的水平位置坐标， mm ;a 为接触区域半径， mm ;E1 、E2 分别为两材料的弹 性模量， MPa;v1 、v2 分别为两材料的泊松比; R1 、R2 分 别为两试样接触表面的曲率半径， mm。

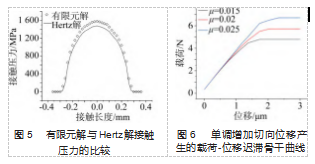
　　取第 1 分析步的最后一步， 压力p=30 MPa 完全加载 时的接触压力数据，将接触正压力的 Hertz 接触解析解和 有限元解进行对比， 结果如图 5 所示。由图可知， 有限 元解的分析结果与 Hertz 接触理论计算的接触压力有一定的偏差，相差 4%，在允许范围之内，说明了所建立的有 限元模型的正确性。

　　3 不同工况条件下能量耗散分析

　　特殊螺纹接头在井下服役时， 由于井下各种工况的 影响， 油管接头承受切向交变载荷及内外压力共同作用， 所以需要分析不同工况条件对特殊螺纹接头密封面处能 量耗散的影响。本文研究对象选择接头密封方式为球 面-锥面密封的特殊螺纹接头，并对其进行简化，建立了 球面-平面接触的简化模型， 分析不同工况条件下球面- 平面接触模型接触面处能量耗散对模型密封性的影响。

　　3.1 迟滞骨干曲线分析

　　当接触面处受切向载荷作用时， 该接触面处将发生 由整体黏着状态向滑移状态的转变， 这种转变导致接触 面处产生载荷-位移迟滞关系。切向载荷变化所引起的 接触面处能量耗散由载荷-位移迟滞曲线所包围的面积 表示， 当接触面受到从 0 开始的单调增加的切向载荷作用 时，加载过程中的载荷-位移曲线称之为迟滞骨干曲线[20]。

　　图 6 所示为通过 Abaqus 得到的具有不同界面特性的 模型所受到的切向载荷和接触区域位移的关系曲线。可 以看出， 随着施加的切向载荷从小到大， 骨干曲线明显 分为线性-非线性-常数 3 段。其中， 线性段为整体黏着 段， 非线性段为微滑过程， 最后的常量水平段为宏观滑 移过程[4]。根据单增载荷下微滑曲线的斜率可以看出， 由于外载荷的增大， 结构整体在切向呈现刚度软化的非 线性特征。由图可知， 摩擦因数越大， 可承受的宏观滑 移载荷也越大。

　　3.2 迟滞曲线分析

　　前文得到了所研究模型的载荷-位移骨干曲线， 施 加循环载荷进一步得到对应的载荷-位移迟滞曲线， 可 更深入理解摩擦界面的动力学特征。施加周期性的切向 位移 s所引起的接触面处能量耗散由载荷-位移迟滞曲线 所包围的面积表示， 在 Abaqus 软件中提取接触区域的位 移与摩擦力， 分别以位移和摩擦力作为横轴与纵轴， 可 以得到加载过程中的载荷-位移迟滞曲线。

　　3.2.1 不同切向位移下的分析

　　由前文可知， 可根据有无宏观滑移区分部分滑移状 态和完全滑移状态。不同切向位移下滑移状态如图 7 所示。由图可知， 摩擦因数 μ =0.02. 压 力 p=30 MPa 时， 当位移 s=2.5×10-4 mm 时开始出现宏观滑移。所 以当位移小于 2.5×10-4 mm 时， 为部分滑移状态; 当 位 移 大 于 2.5×10-4 mm 时 ， 为完全滑移状态。以下将 分别从部分滑移状态和完全滑移状态2个部分研究不同切向位移对能量耗散的影响。

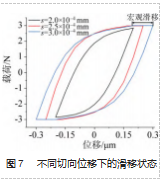
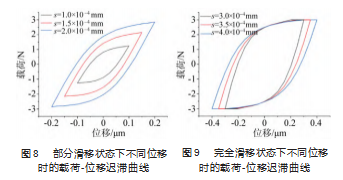
　　选取摩擦因数 μ=0.02. 压力p=30 MPa， 切向位移 s 分别为 1.0×10-4 、1.5×10-4 和 2.0×10-4 mm，得到部分滑移 状态的迟滞曲线如图 8所示; 切向位移 s 分别为 3.0×10-4、 3.5×10-4 和 4.0×10-4 mm， 得到完全滑移状态的迟滞曲线 如图 9 所示。图中迟滞曲线的面积大小代表着接触区域 不同切向位移 s 下的能量耗散的大小。由图 7~8 可知， 在 相同的压力p 下， 当接触区域处于部分滑移状态和完全 滑移状态下时， 接触区域的能量耗散值均随着切向位移 的增大而增大;随着切向位移的增大，接触区域从部分滑 移状态向完全滑移状态转化，其能量耗散值也随之增大。因为球面-平面接触的接触压力是非均匀的， 球面- 平面接触可看成一系列无限小的平面单元， 而法向力的 大小则由压力分布确定， 球面-平面接触的摩擦力分布 如图 10 所示。当接触区域处于部分滑移状态时， 切向位 移相同时， 在接触区域外部的单元法向载荷小， 已经处 于滑动状态， 而内部单元法向载荷大，仍处于黏着状态; 当切向位移增大时，接触区域处于滑动状态的单元增多， 相应地处于黏着状态的区域减少， 所以能量耗散随之增 大， 但未发生宏观滑移[19]。当接触区域处于完全滑移状 态时， 由图 9 可以明显看出存在斜率为 0 的位置，表明发 生了宏观滑移， 所以摩擦力不变; 当切向位移增大时，发生宏观滑移时摩擦力 大小相同， 滑移距离增 大， 导致摩擦力做功增 大， 所以能量耗散值随 之增大。

　　3.2.2 不同压力下的分析

　　不同压力下滑移状态如图 11 所示。由图可知， 摩擦 因数μ=0.02. 位移 s=2×10-4 mm 时， 当压力p=25 MPa 时，开始出现宏观滑移。所 以当压力 p 大于 25 MPa 时 ， 为部分滑移状态 ; 当压力p 小于 25 MPa 时， 为完全滑移状态。以下 将分别从部分滑移状态 和完全滑移状态两个部 分研究不同压力对能量 耗散的影响。

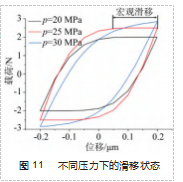
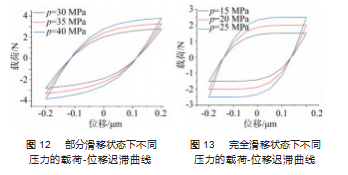
　　选取切向位移 s=2×10-4 mm， 摩擦因数μ=0.02. 压力 p 分别为 30 、35 、40 MPa， 得到部分滑移状态的迟滞曲 线如图 12所示; 压力p 分别为 15 、20 、25 MPa， 得到完 全滑移状态的迟滞曲线如图 13 所示。由图 12~13 可知， 当接触区域处于部分滑移状态和完全滑移状态时， 接触 区域的能量耗散值随压力p的增大而增大; 且当切向位 移幅值一定时， 随着压力p 的增大， 接触区域从完全滑 移状态向部分滑移状态转化。这是因为当压力 p 增大 时， 接触区域内黏着区域随之增大， 相应的滑移区域减 少， 相对滑移减少， 弹性变形量增加， 向部分滑移状态 转化。而且摩擦因数一定， 接触区域内接触压力增大， 摩擦力增大， 导致摩擦力做功增大， 所以能量耗散值也 随之增大。

　　3.2.3 不同摩擦因数下的分析

　　当切向位移 s=2×10-4 mm， 压力 p=30 MPa 时， 分别选取摩擦因数 μ 为 0.015、0.02 和 0.025. 得 到 的 迟滞曲线如图 14 所示。由图可知， 随着摩擦因数的减小， 载荷 -位移迟滞曲线出现了刚度软化现象。还可以看出接触区域的摩擦因数增大时， 引起滑移所需要的切向载荷也需要相应增大。因为在相同法向压力的情况下， 摩擦因数大 的界面， 阻碍滑移的能力更强。

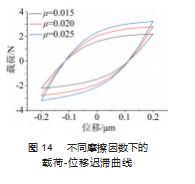
　　由图 14 可得， 接触区域的能量耗散值随摩擦因数μ 的增大而增大。这是因为当压力p 和切向位移载荷幅值 s 一定时， 随着摩擦因数的增大， 接触区域所受摩擦力增 大，导致摩擦力做功增大， 引起的能量耗散也随之增大。

　　4 不同压力下密封性能分析

　　针对特殊螺纹接头金属对金属密封结构， 传统的设 计理念认为， 只要密封面上平均接触应力大于拟密封的 管内流体压力， 金属对金属密封结构即符合密封性能要 求。但是， 按此密封性评价准则设计的金属对金属密封 结构仍产生泄漏。为此， 针对球面-锥面接触密封的形 式， 本文采用密封接触强度模型来评价特殊螺纹接头的 密封性能。

　　基于密封接触能理论， Murtagian通过实验与数值模 拟研究， 建立了一种加权的密封接触强度模型来评估金 属之间的密封性能[12] ，模型为：

　　式中：pav 为平均接触压力， MPa; W 为密封强度; l 为密 封面接触长度，mm;m 为相关性指数， 当使用密封脂时， m=1.2. 当未使用密封脂时，m=1.4.在此处选取 m=1.4.

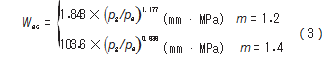
　　式中： Wac 为临界密封强度;pa 为大气压力， 在此处取标 准大气压， 为 0.1 MPa;pg 为拟密封气体压力， MPa。

　　对于高温高压油气井，Xie等[13]综合考虑金属密封结 构和实际密封失效历史数据， 进一步采用有限元方法模 拟了金属对金属密封面接触应力， 对式(3) 进行了优 化，建立了临界密封强度模型：

　　当密封结构的密封强度超过临界密封强度时， 可认 为特殊螺纹具备了足够气密封能力。

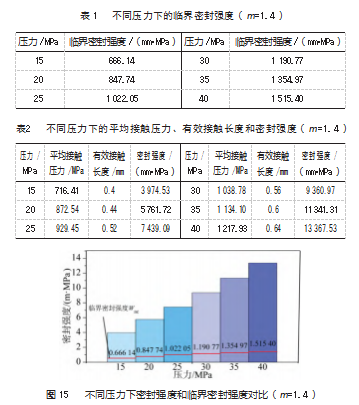
　　根据式(4) 可以得出不同压力 p 下的临界密封强 度， 结果如表 1所示。平均接触压力和有效接触长度是 在有限元模型中提取并计算出来的， 再利用式(2)， 可 计算出不同压力p 作用下球面-平面接触模型的密封强度 W，结果如表 2 所示。不同压力下密封强度与临界密封 强度的对比如图 15所示， 图中柱状图为不同压力下的密 封强度， 红线为不同压力下的临界密封强度。由图可知， 在不同压力p 下， 密封强度均大于临界密封强度。由此 说明， 当压力 p 处于 15~40 MPa 时， 均满足密封要求。 由图 15 可明显得出， 随着压力p 的不断增大， 密封强度 也随之增大，说明密封性能也随之提高。

　　5 结束语

　　基于特殊螺纹密封面处球面-锥面密封结构， 建立 了球面-平面接触的有限元简化模型， 并通过对接触压 力的有限元解和解析解进行比较，验证了模型的合理性。 在 ABAQUS 软件中提取接触区域的位移与摩擦力， 得到 加载过程中的能量耗散的迟滞骨干曲线和迟滞曲线， 分 析了接触区域切向位移 s、压力p 和摩擦因数对能量耗散 的影响; 并通过密封接触强度理论对接触区域密封性能 进行了分析， 主要得出以下结论。

　　( 1) 由载荷-位移迟滞骨干曲线可以得出， 摩擦因 数越大， 可承受的宏观滑移载荷也越大; 且随着载荷的 增大，呈现出刚度软化现象。

　　(2) 由载荷-位移迟滞曲线可以得出，部分滑移状态 和完全滑移状态下，接触区域的能量耗散值都与切向位移 s、压力p 和摩擦因数呈正相关关系，密封性能有所降低。

　　(3) 由密封强度理论分析可得， 当压力p 处于 15~ 40 MPa 时， 均满足密封要求; 随着压力p 的增大， 密封 接触强度增大， 密封性能随之提高。

参考文献：

　　[1] MATTHEWS C. Assessing tubular connection leakage integrity [J]. World Oil, 2002. 223(2): 82-84.

　　[2] 许志倩,闫相祯,杨秀娟 . 特殊螺纹套管接头连接性能的安全 可靠性分析[J].北京科技大学学报,2011.33(9):1146-1153.

　　[3] 莫丽,涂炼,付强,等 .特殊螺纹接头双主密封结构密封性能分 析[J].润滑与密封,2018.43(2):87-93.

　　[4] 孙德林 . 螺栓连接结构能耗机理及预示研究[D].北京:北京理工大学,2016.

　　[5] SHAMOTO E, HASHIMOTO Y, SHINAGAWA M, et al. Analyti ‐ cal prediction of contact stiffness and friction damping in bolted connection[J]. CIRP Annals, 2014. 63(1): 353-356.

　　[6] 张颖,练章华,周谧,等 . 高压高产气井油管柱特殊螺纹密封动力 学研究[J]. 中国石油大学学报(自然科学版),2020.44(3):134-140.

　　[7] XIAO H F, SHAO Y M, XU J W. Investigation into the energy dissipation of a lap joint using the one-dimensional microslip friction model[J]. European Journal of Mechanics - A/Solids, 2014. 43: 1-8.

　　[8] 李凡,王夫军,窦益华,等 .特殊螺纹接头密封面能量耗散与密 封特性研究[J].石油机械,2022.50(11):140-146.

　　[9] 曹银萍,刘渝,于洋,等 . 气密封检测对特殊螺纹油管接头密封 性能的影响[J].机电工程技术,2023.52(3):77-79.

　　[10] 陈宇杭,练章华,丁亮亮,等 .基于 ABAQUS 的特殊螺纹接头优 选[J].科学技术与工程,2022.22(33):14714-14721.

　　[11] 刘祥康,杨建,杜明海,等 . 高温高产井油管屈曲对特殊螺纹性 能的影响[J].科学技术与工程,2022.22(36):16024-16031.

　　[12] MURTAGIAN G R, FANELLI V, VILLASANTE J A, et al. Seal ‐ ability of stationary metal-to-metal seals[J]. Journal of Tribolo ‐ gy, 2004. 126(3): 591-596.

　　[13] XIE J R, RONG F, DESSEIN T. Methodology for reliability- based design and assessment of tubular connection sealability in HPHT wells[C]//Proceedings of International Conference on Oil Country Tubular Goods and Tubular String. Xi'an, 2014.

　　[14] 曾威 ,宋红 ,解欢 ,等 . 基于密封接触强度的水下井口连接器 VX钢圈密封特性分析[J].润滑与密封,2019.44(8):121-126.

　　[15] YU Y, QU Z, CAO Y P, et al. Sealability analyses of premium connections characterized by a surface fractal function[J]. Ap plied Sciences, 2023. 13(11): 6467.

　　[16] YUE T Y, ABDEL WAHAB M. Finite element analysis of fret ‐ ting wear under variable coefficient of friction and different con ‐ tact regimes[J]. Tribology International, 2017. 107: 274-282.

　　[17] 齐俊林,罗维东,张宏,等 . 圆螺纹套管接头上扣与滑脱的数值 模拟[J].石油大学学报(自然科学版),1998.22(4):68-71.

　　[18] DONE V, KESAVAN D, KRISHNA R M, et al. Semi analytical fretting wear simulation including wear debris[J]. Tribology In ‐ ternational, 2017. 109: 1-9.

　　[19] 周仲荣,Leo Vincent. 微动磨损[M].北京:科学出版社,2002.

　　[20] SEGALMAN D J. Modelling joint friction in structural dynam ‐ ics[J]. Structural Control and Health Monitoring, 2006. 13(1): 430-453.