磁流变脂动态非线性滞回特性/应变增强效应的参数建模论文
2022-11-18 14:23:27 来源: 作者:shaozhun
摘要:摘要:为了充分发挥基于磁流变脂材料的功能器件的半主动控制,需要寻找一个高精度的模型来实时、准确地预测其动态流变特性,以便采取适当的控制策略来提高结构的响应。建立合适的参数模型预测磁流变磁控智能软材料的动态流变行为,是在工程上实现其半主动控制的基础,研制出新型磁流变材料——磁流变脂,并对其动态特性展开测试。基于对测试结果的讨论,采用遗传优化算法,利用Bouc-Wen参数模型来描述这种非线性迟滞现象(应变增强效应),并进行参数建模及识别,利用建立的模型进行不同温度下滞回曲线的预测。结果表明:随着应变的增大,磁
摘要:为了充分发挥基于磁流变脂材料的功能器件的半主动控制,需要寻找一个高精度的模型来实时、准确地预测其动态流变特性,以便采取适当的控制策略来提高结构的响应。建立合适的参数模型预测磁流变磁控智能软材料的动态流变行为,是在工程上实现其半主动控制的基础,研制出新型磁流变材料——磁流变脂,并对其动态特性展开测试。基于对测试结果的讨论,采用遗传优化算法,利用Bouc-Wen参数模型来描述这种非线性迟滞现象(应变增强效应),并进行参数建模及识别,利用建立的模型进行不同温度下滞回曲线的预测。结果表明:随着应变的增大,磁流变脂的滞回曲线逐渐向非线性过渡,直到应变为10%和100%时,具有明显的非线性黏弹性特性;随着应变幅值的增大,材料的滞回曲线的非线性表现出应变增强效应;模型具有较高的建模精度,能够很好地描述磁流变脂在各种应变幅值下的独特而复杂的行为,为基于这种材料的结构装置在振动控制中的应用提供理论参考。
关键词:磁流变脂;滞回曲线;应变增强;Bouc-Wen模型;遗传算法;温度
Abstract:In order to give full play to the semi-active control of functional devices based on magnetorheological grease,it is necessary to find a high-precision model to accurately predict the dynamic rheological properties of the material in real time,so as to adopt appropriate control strategies to improve the response of the structure.Establishing a suitable parameter model to predict the dynamic rheological behavior of magnetorheological magnetron intelligent soft materials is the basis for realizing its semi-active control in engineering.A new type of magnetorheological material magnetorheological grease was developed and its dynamics performances were test.Based on the discussion of the test results,genetic optimization algorithm was used,Bouc-Wen parameter model was used to describe this nonlinear hysteresis phenomenon(strain enhancement effect),and the identification of parameter modeling was performed.Furthermore,the model was used to description the hysteresis curve at different temperatures.The results show that with the increase of strain,the hysteresis curve of magnetorheological grease gradually becomes nonlinear,until the strain is 10%and 100%,it has obvious nonlinear viscoelastic characteristics.With the strain amplitude increases,the nonlinearity of the hysteresis curve shows a strain-enhancing effect.The model has high modeling accuracy and can well describe the unique and complex behavior of magnetorheological grease under various strain amplitudes.It provides a theoretical reference for the application of structural devices based on this material in vibration control.
Key words:magnetorheological grease;hysteresis curve;stiffening;Bouc-Wen model;genetic algorithm;temperature
引言
磁流变材料的性质可以通过外部磁场持续、快速和可逆地改变[1-3]。一般来说,磁流变材料分为磁流变液、磁流变弹性体、磁流变脂和磁流变泡沫[4]等。磁流变液是一种常见的智能材料,由于其流变特性的可调性,特别是在机械阻尼器、减振器、执行器等工程应用中,受到了广泛的关注[5]。然而,磁流变液中发生的颗粒沉积问题导致磁流变效应的降低,同时也限制了其在应用中的可用性[6-7]。因此,有人提出了几种方法来克服这一问题:在磁性粒子上涂覆聚合物[4]、引入纳米粒子作为填料[8-9]、将不同大小的磁性粒子[10]结合在离子液体中[11],添加添加剂或表面活性剂[12]并用触变剂(如二氧化硅)改变悬浮介质[13]。磁流变液技术虽然经过了许多努力,但尚未完全解决这一问题。考虑到这一点,选择润滑脂作为高黏度的载体流体,以消除沉淀问题[14]。
磁流变脂是将软磁颗粒均匀分散在润滑脂中形成的一种复合磁响应材料,是磁流变材料中的一种,具有如下流变特性:在磁场作用下,基体中的软磁性颗粒瞬间被磁化,并沿着磁场方向成链,具有一定的磁控剪切屈服应力和表观黏度,一旦外部磁场消失,其软磁性颗粒又重新回到原来的均匀分布状态,因此该过程具有可逆、快速、连续特性,在阻尼器、离合器、制动器、抛光装置中具有潜在应用价值[15]。
虽然磁流变脂在振动控制中有着广阔的应用前景,但其工程应用的主要挑战是这种半主动装置的非线性和滞后现象。为了更好地设计磁流变脂功能器件的控制方法,首先需要寻找一个可靠有效的模型。然而,到目前为止,很少有人提出模型来描述这种独特的特性。目前发展起来的模型通常分为两类:非参数模型和参数模型。非参数模型总能提供准确度高、适应性强的器件响应预测结果。一般来说,这类模型是基于人工智能方法设计的。在这些模型中,需要训练样本来调整模型的结构参数以获得精确的模型。然而,非参数模型的主要缺点是模型参数没有任何物理意义。
另一方面,参数化模型可以解决这一问题,其中模型参数总是具有特定的物理意义。在参数模型中,最经典的是Bouc-Wen模型,由Bouc在1971年提出[16]。在Bouc-Wen模型中,采用高度非线性微分方程来产生滞回环。通过引入中间参数,提高了模型的精度。基于这种迟滞模型,已经发展了几种现象模型来捕捉不同磁流变元件的迟滞行为。例如Behrooz等[17]提出了一个带有粘滞阻尼器、弹簧和迟滞Bouc-Wen分量的现象模型,以说明基于磁流变弹性体的变刚度阻尼隔离器的阻尼、刚度和滞回特性。在该模型中,上升磁场通过电流相关阻尼、电流相关弹簧和电流相关Bouc-Wen单元增加阻尼、刚度和滞回特性。此外,Yang等[18]提出了一种新的现象学模型来描述磁流变基底隔离器的独特行为。该模型将Bouc-Wen单元和Voigt元件并联接合,描述了滞后曲线,再现了器件的固体材料行为。因此Bouc-Wen模型能够较好的描述材料及器件中存在的非线性滞回特性。
磁流变脂作为新型磁流变智能材料,在工程应用中具有潜在应用价值。因此,针对磁流变脂流变力学行为的建模研究具有一定的价值和意义。本文主要针对磁流变脂的应力-剪切应变、应力-剪切速率的滞回曲线,基于遗传优化算法,利用Bouc-Wen模型对其展开力学特性的参数建模和参数识别。以其找到一种能够较好预测不同应变幅值下磁流变脂非线性滞回流变行为,为磁流变脂的可控性工程应用化具有一定的理论参考价值。
1磁流变脂动态流变行为测试
研制羰基铁粉质量分数为60%的磁流变胶脂。利用安东帕生产的型号为MRC302流变仪,在室温条件(25℃)下对研制的磁流变脂应力-应变、应力-应变速率曲线进行测试。测试条件为:施加电流为2 A下,频率稳定在0.1 Hz(准静态);准静态为材料工作的特殊状态,具有更加明显的非线性特性,因此本文选择在准静态工作环境下得到的滞回曲线展开模型预测。应变幅值分别为0.01%、0.1%、1%、10%和100%。在测试过程中设置流变仪两平板之间的距离为1 mm,流变仪两测试平板直径为20 mm。测试得到电流为2 A条件下,在准静态环境中应变幅值分别为0.01%、0.1%、1%、10%和100%的应变幅值/速率-应力,分别如图1~5所示。
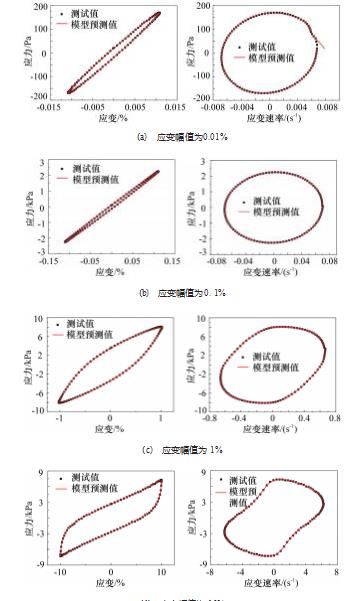
在准静态条件下,电流为2 A的时候,磁流变脂滞回曲线的黏弹性特性随着应变幅值变化非常明显。如在应变幅值为0.01%和0.1%的时候,磁流变脂的应力-应变曲线为一具有一定斜度的椭圆状,表现出线性黏弹性特性;但进一步增大应变幅值到1%的时候,其滞回曲线逐渐向非线性过度,直到应变为10%和100%时,具有明显的非线性黏弹性特性。这是由于应变幅值很小的时候,在剪切过程中颗粒之间的拉伸距离足够小,发生弹性变形,因此对外表现出线性黏弹性特性,随着应变幅值逐渐增大,颗粒之间被拉伸的距离大于弹性变化范围,发生不可逆挪位,宏观上表现出非线性特性。另外,磁流变脂的黏度分量(滞回曲线包络的面积)和弹性分量(滞回曲线最大应力和最小应力之间的连接线)都随着应变幅值增加而增大。但是在实际工作过程随着工作环境,比如说应变幅值的变化,使得材料不停地在线性黏弹性和非线性黏弹性区域往复工作,因此需要寻找一个参数模型能够同时预测材料这种线性黏弹性和非线性黏弹性行为,为实现磁流变脂的半主动控制提供理论指导。
另外非常值得注意的是随着应变幅值的增大,材料的滞回曲线的非线性表现出应变增强效应,如在应变幅值为10%的情况下,其放大如图2所示。但是在实际工作过程随着工作环境,比如说应变频率的变化,使得材料的黏弹性不断发生变化,因此需要寻找一个参数模型能够预测材料这种具有应变增强效应的黏弹性行为,为实现磁流变塑性体在工程应用中的半主动控制提供理论指导。
2 Bouc-Wen参数模型
如图3所示,Bouc-Wen模型首先是由Bouc和Wentic提出的用于构建磁流变行为中的应力-应变滞回特性。由图可以看出Bouc-Wen模型由Bouc-Wen算子和一个弹性单元和一个黏性单元并联组成。因此,该模型中输出
应力与输入应变的关系可以表示如下:
τpre=αz+k 1(x-x0)+c 1 ẋ(1)
式中:x和ẋ分别为剪切应变和剪切速率;k1和c1分别为弹性单元和黏性单元;x0为初始位移;z为滞回算子,其具体表达式如下:
ż=Aẋ-βẋ|z|n-γ|ẋ|z|z|n-1(2)
式中:ż为z对时间的微分;A、β和γ为模型形状控制参数;n为滞回曲线平顺系数。
因此,Bouc-Wen模型中有如下8个参数需要被优化识别:
∪=[A、β、γ、n、α、k 1、c 1、x0]
由于遗传算法(具有编码简单、收敛速度快的特点,采用GA求解参数优化问题。另外,到目前为止GA已用于Bouc-Wen模型的参数辨识,能够较好地预测磁流变阻尼器动态输出特性曲线。其原理描述如下:
(1)读取剪切应力、剪切应变和剪切速率;
(2)确定适应度函数,设置染色体数N=30,交叉率pc=0.70,变异概率pm=0.03,有限迭代次数X=100;
(3)确定模型参数,初始化模型参数值;
(4)为每个模型参数初始化一组染色体;
(5)利用适应度函数值对每条染色体进行评价,并与前一条染色体进行比较;
(6)利用轮盘赌法对染色体进行适合度排序选择新的群体;
(7)应用交叉和突变更新染色体;
(8)评估新染色体,并检查是否符合终止标准,如果满足停止条件或迭代次数大于有限的迭代次数,则输出最佳染色体作为解并输出最佳模型参数值,否则,返回步骤4。
采用遗传优化算法,利用模型计算所得应力与实测应力之间的均方根值作为算法适应性函数,如下所示:f=×100%式中:f为模型满意度;N为数据个数;Fn为第n个点的模型预测值;τn为第n个点的实测值。
3结果与讨论
利用Bouc-Wen参数模型对磁流变脂在不同应变幅值的滞回曲线进行模型预测,结构如图4所示,对应的模型参数优化结构如表1所示。由图可以看出Bouc-Wen参数模型能够较好预测磁流变脂的线性黏弹性特性和非线性黏弹性特性。但应变幅值为0.01%的时候(非常小),因此,在测试中一个小小波动就会产生较大的影响。针对应力-应变速率,Bouc-Wen参数模型存在一小段预测偏离较大的范围,而这一段恰恰是应变速率最大,所对应的是应变刚开始的时候,在这时候测试值存在一定的偏离,因此,而模型预测适应函数的其中一个变量为测试值,进而对模型预测产生一定的误差。但应变幅值进一步增大,由图可以看出无论是针对材料的应力-应变曲线还是应力-应变速率曲线模型都具有较好的预测能力。因此可以说明在测试范围之内,利用遗传算法寻找最优参数值后,Bouc-Wen模型能够用来描述磁流变脂动态滞回行为,为其在工程应用中提供理论基础。
颗粒在磁场作用下形成链/柱状,具有一定的剪切屈服应力,磁流变器件的减振原理是当外部作用力大于该应力的时候,链/柱状被破坏,将机械能转换成颗粒之间或者颗粒与基体之间的内能,进而导致磁流变材料的温度上升,影响控制精度和可靠性。因此需要证明Bouc-Wen模型针对在不同温度下磁流变脂动态滞回曲线的预测能力是否满足要求。图5所示为在不同温度下(应变幅值为10%),磁流变脂动态滞回曲线测试值和模型预测值的比较。结果表明,提出的Bouc-Wen参数模型能很好地反映磁流变脂在不同温度下的非线性滞回特性和应变增强特性。因此,所提出的参数模型为磁流变脂能够在不同温度下可控提供控制基础。
4结束语
本文自行研制羰基铁粉质量分数为60%的磁流变胶脂。利用安东怕生产的型号为MRC302流变仪对其动态滞回响应(应力-应变、应力-应变速率)展开应变幅值分别为0.01%、0.1%、1%、10%和100%的测试。测试结果表明磁流变脂的黏弹性特性随着应变幅值发生明显变化,具有复杂的流变行为。基于遗传优化算法,利用Bouc-Wen参数模型来描述这种复杂的非线性迟滞现象,并进行参数识别。结果表明,该模型具有较高的建模精度,能够很好地描述磁流变脂在各种应变幅值下的独特而复杂的行为。其次,该参数模型能够很好地反映磁流变脂在不同温度下的非线性滞回特性和应变增强特性。为基于该材料的结构装置在振动控制中的应用提供理论参考。
参考文献:
[1]胡晨,路家斌,肖晓兰,等.氧化锆陶瓷球磁流变抛光工艺试验研究[J].机电工程技术,2020,49(10):42-44.
[2]Fang F,Choi H,Jhon M.Magnetorheology of soft magnetic car⁃bonyl iron suspension with single-walled carbon nanotube addi⁃tive and its yield stress scaling function[J].Colloids and Surfaces A Physicochemical and Engineering Aspects,2009,351(1-3):46-51.
[3]童和平,张香红,张洲,等.单晶SiC抛光用磁流变液稳定性研究及应用[J].机电工程技术,2018,47(2):126-129.
[4]张广,汪辉兴,欧阳青,等.硅树脂基磁流变胶流变特性研究及Herschel-Bulkley模型参数识别[J].湖南大学学报(自然科学版),2018(6):62-71.
[5]张冲,鲁刘磊.磁流变液矩形夹层板的动力特性分析[J].机电工程技术,2013,42(2):15-20.
[6]Meharthaj H,Sivakumar S M,Arockiarajan A.Significance of particle size on the improved performance of Magnetorheological Gels[J].Journal of Magnetism and Magnetic Materials,2019:165483.
[7]杨延荣,单慧勇,卫勇.圆筒式磁流变制动器的理论设计与分析[J].机电工程技术,2005(10):22-23.
[8]黄炼,查长松.磁流变弹性体的磁致性能[J].材料科学与工程学报,2016,34(1):139-141.
[9]Li Y,Li J,Li W.A state-of-the-art review on magnetorheologi⁃cal elastomer devices[J].Smart Mater.Struct,2014,23 123001.
[10]Behrooz M,Wang X,Gordaniejad F.Modeling of a new semi-active/passive magnetorheological elastomer isolator[J].Smart Mater.Struct.2014,23 045013.
[11]廖君华.端部控制磁流变液阻尼器实验研究[J].应用力学学报,2017,34(3):583-588.
[12]Yu Y,Li Y,Li J.Parameter identification of an improved Dahl model for magnetorheological elastomer base isolator based on enhanced genetic algorithm[C]//Proc.ACMSM 2014(Byron Bay):931-936
[13]崔立辉,薛德庆,刘长江,等.圆盘式磁流变离合器的设计计算[J].机电工程技术,2011,40(8):99-102.
[14]李秀领,李宏男.磁流变阻尼建筑结构多态控制策略研究[J].应用力学学报,2008(1):162-167.
[15]Jimenez R,Alvarez-Icaza L.LuGre friction model for a magneto⁃rheological damper[J].Struct Control Hlth,2005(12):91-116
[16]司鹄,彭向和,陈伟民.分析磁流变流体屈服应力微观力学模型[J].应用力学学报,2005(2):198-201.
[17]Jolly M R,Carlson J D,Munoz B C.A model of the behaviour of magnetorheological materials[J].Smart Materials and Struc⁃tures,1996(5):607.
[18]龚政,马平,陈爱民.基于有限元方法的磁流变阻尼器多目标优化设计[J].机电工程技术,2010,39(3):44-47.










