摘要：针对滚动轴承的机械故障诊断问题，提出一种小波包能量谱-偏最小二乘(PLS)故障检测法。依据小波包分解后可以将振动信号分解到各自不同的频率段上的特点，对实验中采集的振动信号进行分解，进而从经小波包分解后的独立频段上各自提取能量谱，并构建能量谱特征向量，能量谱特征向量的变化反映了运行状态的改变。对得到的能量谱特征向量进行偏最小二乘分析，建立故障检测模型，利用T2及SPE统计量来判断被测轴承是否发生故障。试验表明：与单纯的小波包分析法和偏最小二乘法相比，所提方法具有故障检测结果更加直观、高效的特点，此方法是可行且有效的。

　　关键词：滚动轴承；小波包；偏最小二乘(PLS)；故障检测

　　Abstract:To solve the problem of mechanical fault diagnosis of rolling bearings,a partial least squares method(PLS)fault detection method with wavelet packet energy spectrum is proposed.According to the feature that the vibration signals can be decomposed into different frequency segments after the decomposition of wavelet packet,the vibration signals collected in the experiment are decomposed,and then the energy spectrum is extracted from the independent frequency band after the decomposition of wavelet packet,and the energy spectrum feature vectors are build,the change of the energy spectrum feature vectors reflects the change of bearing in running state.The partial least squares analysis is carried out on the obtained energy spectrum feature vector,and a fault detection model is established.T2 and SPE statistics are used to detect and determine whether the bearing under test is faulty.The test verification shows that compared with the simple wavelet packet analysis method and partial least square method,the proposed method is more intuitive and efficient,which is feasible and effective.

　　Key words:rolling bearing;wavelet packet;partial least squares(PLS);fault detection

　　0引言

　　滚动轴承作为机械设备的重要组成部分，在生产设备中有着不可或缺的地位，相关研究表明机械设备的旋转部件中约30%的故障都是由滚动轴承引起的[1]，因此对滚动轴承进行故障检测，保证其正常运行，有着极其重要的意义。滚动轴承在运行过程中会产生机械摩擦，并因此对外发出特有的信号，所以对其进行数据采集[2]并利用各种分析方法对采集到的振动信号进行研究是现阶段一种常规的有效方法[3]。

　　分析研究表明，信号各频带的能量信息变化是由于滚动轴承在发生了某些问题后所传达的故障信息，最明显的是各个不同频带的能量在总的频带能量比例中的占比会发生明显的变化，可以利用此显著变化来分析轴承的运行状况[4]。但是，对某些故障，此方法不能够直观明显地表现出来，因此单独使用于故障检测效果较差。小波包分析可将信号分解在不同的尺度上，不仅可提取信号在不同频带上的频域特征，同时又能保留信号在各个尺度上的时域特征，因而可对原始振动信号进行小波包分解，并从中提取轴承信号的能量特征信息[5]。

　　因此，以振动信号各频带的能量值为分析依据[6]，本文提出一种小波包能量谱――偏最小二乘(Partial Least Squares Method，PLS)故障检测方法。首先，依据原始滚动轴承信号经小波包分解后得到的各个独立特有频段，研究各子频带能量值的变化可以反映出系统运行过程中发生的变化；其次，依据上述分解得到的特征向量，对其进行偏最小二乘分析，并用相关的标定值对轴承故障进行检测；最后，利用已公开的权威数据对上述理论模型进行实验仿真，测试此方法的可行性。

　　1振动信号特征提取

　　1.1小波包分解

　　根据前文所述小波包分解的特点，对待分析振动信号数据进行多层次的分解，即在小波的基础上对高频部分进行进一步的分解，根据得到的信号频谱，自行选择对应频段，以此方法来提高被研究信号在时频上的分辨率[7]。

　　利用小波包研究实验数据时，小波包分解层数视具体情况要求而定。分解后各频段的频率范围如式(1)所示。

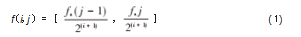
　　式中：f(i,j)为第i层分解的第j频带的频率段范围(j=1，2，…，2i)；fs为采样频率。

　　在滚动轴承故障检测过程中，先对数据信号进行小波包分解，对其进行3层分解就得到8个频率段，这些频率段里面包含有所需要的信息。

　　对数据信号小波分解后再进行系数重构。通过s(j=0,1,…,7)，提取得到各不同子频段信号，因此总信号可表示为式(2)。

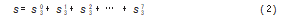
　　1.2小波包能量谱

　　按照能量谱值来反映被分析数据的隐含特征，这是小波包能量谱的独特之处。在小波包变换中，原始信号f(x)在L2(R)上的2范数定义为：

　　各子频带对应的能量值为：

　　式中：xjk(j=0,1,…,7;k=0,1,…,n)为重构信号s离散点的幅值。

　　因此根据小波包变换原理，原始数据信号时域能量

　　等于变换数据信号2范数的平方，即存在：

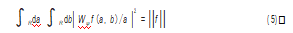
　　从上式可以看出经小波包分解后的能量与原始信号的能量之间存在等价关系，因此利用小波包分解后的能量谱表示原始信号的能量是可行的[8]。所以由式(4)可以求得重构后以能量值表示的特征向量T，如式(6)所示。

　　T=[E,E,…,E,E]                         (6)

　　2偏最小二乘法

　　PLS是一种新型多元统计数据分析方法，在现实生产中应用极其广泛。它的主旨思想是将原始数据从高维空间投影到低维空间，利用第一主成分提取后所剩余残差数矩阵信息替代原始数据，再以此数据进行第二主成分提取。

　　不断重复以上步骤直至达到约束条件的要求。它集成了主成分分析法、典型相关性分析法以及线性回归方法的特点。偏最小二乘法与主成分法最大的不同之处在于得分因子的提取方法不同。简而言之，主成分分析预测变量X之间的协方差需要靠产生的权重矩阵来进行反映，而PLS预测变量X与响应变量Y之间的协方差[9]是靠产生的权重矩阵反映。

　　PLS需要输入矩阵X(X∈Rn⋅m)和输出矩阵Y(Y∈Rn⋅m)，针对输入和输出矩阵，在考虑了输出得分向量U和输入得分向量T所代表的内在之间的线性关系的基础上[10]，对相关量进行非独立的主成分分解，从而得到一个包括外部特征模型和内部特征模型的PLS新模型。模型公式如式(7)所示。

　　式中：E(E∈Rn⋅m)和F(F∈Rn⋅p)为残差矩阵，主要是将噪声信息包含在内而建立的新矩阵。因此也可以理解为经过上述变换，已将可以用来预测状态的有用信息主元包含在内。相关研究表明，将此残差空间忽略掉对数据研究来说不会损失相关有用的信息[11]。被研究数据X和Y中的主元值组成特征向量分矩阵，分别为式(7)中的T和U，X和Y对应的负荷向量分别由P和Q组成的负荷矩阵表示。

　　经过迭代转换，进一步建立最终的PLS模型为

　　Y=UQT+F=TBQT+=XPBQT+F(8)

　　式中：θ=PBQT，θ∈Rn⋅p为系数矩阵，B∈Rk⋅k为诊断矩阵。

　　为更有效提取过程数据中的信息，在进行PLS之前先要对数据进行归一化处理[12]，这样可消除因不同量纲或者长度带来的影响，确保波动大的变量元素不占主导地位，把所有的数据都标定到单位方差。PLS模型参数通常可通过非线性迭代偏最小二乘法(NLPALS)计算得到，具体过程见文献[13]。利用PLS对数据建立模型，故障检测中通常的做法是用Hotelling T2检测量值和Q残差检测量值实现，其具体原理见文献[14]。

　　2.1 Hotelling T2检测

　　Hotelling T 2检测统计量是用来估算模型内部的数据变化的。在第i个样本时：

　　Ti2=tiλ-1 t=Xi Pλ-1 PT XiT(9)

　　式中：ti为矩阵Tk的第i行，Tk由K个主元的得分向量组成；λ为主元特征值的平均值；T 2统计量通过计算向量模型的波动反应出变量的变化趋势。T 2统计量的限值服从F分布：

　　式中：m为样本数；α为显著水平。当T 2>T m,α时，显示当前T 2统计量有异常。

　　2.2 Q残差检测

　　Q残差统计也被称为SPE统计，是模型外部变量的波动检测[14]，是样本在残差子空间上投影的平方。

　　SSPE=eT e(11)

　　式中：e为主元模型中的残差空间。

　　正常工况下应满足SSPE<Qα，Qα的计算公式如式(12)所示。

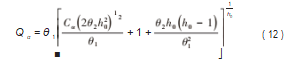
　　式中：Cα为一个高斯分布的(1-α)%的置信极限。

　　3小波包能量谱-偏最小二乘法故障检测

　　本文提出的小波包能量谱-偏最小二乘法，首先对采集到的信号进行小波包分解，求出其能量谱矩阵，再对此矩阵进行PLS分析，进行故障检测。采用db3小波基，对信号进行小波包分解，进行3层分解得到从高到低8个频率段。所提方法步骤如下。

　　(1)首先对振动数据进行小波包分解，按照式(4)求其在不同频率段的能量值E，最终得到特征向量T。

　　(2)以不同频率段的特征向量值T为输入值，通过上述公式计算正常样本数据的均值和标准差，同时对样本数据采用归一化方法处理，得到新的训练样本矩阵。

　　(3)以新构建的训练矩阵建立正常的模型，对其进行PLS分析求得正常数据情况下T2统计量和SPE统计量的控制限。

　　(4)对采集到的测试样本重复步骤(1)~(3)，求取T2和SPE统计量进行故障检测。具体故障检测流程如图1所示。

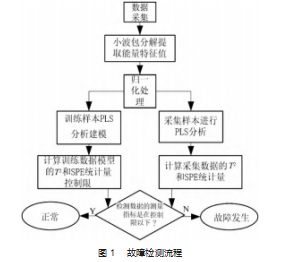
　　4实验研究

　　为验证上述理论建模的可靠性，采用已公开发表的美国Case Western Reserve University的振动信号为样本进行仿真验证，该数据的采集条件及数据详见文献[15]。同时对数据进行时域分析、小波包分析、PLS分析。

　　(1)分别取正常振动信号和故障振动信号，对取得的数据经小波包变换进行时频域分析。正常振动信号、故障振动信号的时域分别如图2~3所示。由图可知，虽然信号的幅值发生了变化，但单凭这些是无法判断故障的，所以对这些数据再进行频域分析。正常振动信号、故障振动信号的频谱分别如图4~5所示。由图可知，2种信号的幅值和频谱分布均发生了变化。

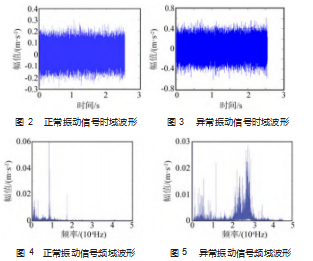
　　(2)选用db3小波基对正常和故障数据进行3层小波包变换，得到8个频率带，计算其中各节点的小波系数，并求出各自的能量值。在对分解得到的子频带能量值相加求和后，根据每一个子解频带的能量值占总信号能量值的百分比来分析各频带的能量占比情况。对比正常振动信号能量比例直方图和异常振动信号能量比例直方图说明两者之间的差异，具体如图6~7所示。由图可知，不同频带的比例发生了变化。

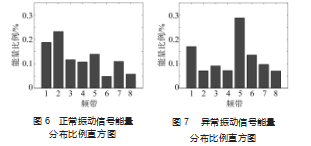
　　(3)对小波包处理后的数据测试数据进行PLS分析，提取相关特征量，并分别求出本文重点需要的主元统计量T2和SSPE，利用这2个量值衡量故障是否发生。从原始的正常和异常信号中分别取600组数据，在进行小波包分解的基础上进行PLS分析，得到T2和SSPE检测结果分别如图8~9所示。由图可知，T 2和SSPE统计量明显发生跳跃，并持续维持在高位值，准确地检测到了故障，验证了此方法的有效性。

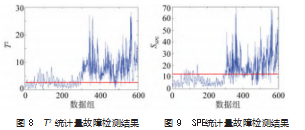
　　5结束语

　　本文提出小波包-偏最小二乘滚动轴承故障检测方法，将采集到的振动信号分解到各自不同的频率段上，在小波包分解后的独立频段上各自提取能量谱，并构建能量谱特征向量，再对得到的能量谱特征向量进行偏最小二乘法分析，建立PLS故障检测模型，进行故障检测。理论分析和实验结果表明，利用该方法进行滚动轴承的故障检测是有效的。分析不同频段小波包能量比例直方图，可以确定在发生故障时，哪些频段发生了变化，为后续研究做铺垫。

　参考文献：

　　[1]WANG B,LEI Y G,LI N P,et al.A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[j].IEEE Transactions on Reliability,2020,69(1):401-412.

　　[2]涂志松.基于小波包和支持向量机的滚动轴承故障诊断[J].机电工程技术,2020,49(12):208-211.

　　[3]马建仓,叶佳佳.基于小波包分析的航空发动机故障诊断[J].计算机仿真,2010,27(2):49-51.

　　[4]王佳方.基于小波包能量谱与神经网络的电子式互感器故障检测系统[D].重庆:重庆理工大学,2021.

　　[5]杨宇,于德介,程军圣.基于EMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2005,24(1):85-88.

　　[6]JENA D P,PANIGRAHI N S.Bearing and gear fault diagnosis us⁃ing adaptive wavelet transform of vibration signals[J].Procedia Engineering,2012(50):265-274.

　　[7]潘丽莎,陈浩等.基于小波包和RBF神经网络的轨道车辆滚动轴承故障检测[J].计算机应用,2012,21(7):8-12.

　　[8]彭恒义,轩建平,史铁林.基于小波包分析的往复式天然气压缩机故障诊断系统[J].机床与液压,2004(7):180-182.

　　[9]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999.

　　[10]BANAKAR A,AZEEM M F.Artificial wavelet neural network and its application in neuro-fuzzy models[J].Applied Soft Com⁃puting.2008(8):1463-1485.

　　[11]MURADORE R,FIORINI P.A PLS-based statical approachfor fault detection and isolation of robotic manipulators industrial electronics[J].IEEE Transactions on Industrial Electronics,2012,59(8):3167-3175.

　　[12]蒋浩天.工业系统的故障检测与诊断[M].北京:机械工业出版社,2003.

　　[13]ROSIPAL R,TREJO L J.Kernel partial least squares Regression in reproducing kernel Hibert space[J].Journal of Machine Learn⁃ing Research,2001,2(6):97-123.

　　[14]LI X,JUN L,QIAN J X.Multivariate statistical process monitor⁃ing of an industrial polypropylene catalyzer reactor with compo⁃nent analysis and kernel density estimation[J].Chinese Journal of Chemical Engineering,2007,15(4):524-532.

　　[15]BOUDIAF A,MOUSSAOUI A,DAHANEA,et al.A comparative study of various methods of bearing faults diagnosis using the case western reserve university data[J].Journal of Failure Analy⁃sis and Prevention,2016,16(2):271-284.