摘要：机械结构类的产品在长期使用过程中，部分零部件会承受各种交变应力，需进行疲劳强度校核，而国内尚无完整的疲劳强度计算校核规范指引。基于疲劳强度的基本理论，详细解释了疲劳强度的基本概念、应力类型和S－N疲劳曲线的应用规则，并分析得出疲劳极限应力图中斜率k与循环应力特征r之间的关系，以及古德曼、修正古德曼、戈倍尔和索德伯格4大平均应力疲劳曲线的理论计算及其应用，诠释了真实应力和工程应力的含义及两者之间的区别，并综合分析疲劳强度的校核规则和要求，推导计算出无限寿命设计疲劳安全率的计算公式，结合国内外研究文献给出无限寿命设计的疲劳安全率判定标准，得出了一种有效的疲劳强度计算理论方法，为机械结构的疲劳强度校核提供了一种有效而准确的理论计算依据。

　　关键词：疲劳强度；古德曼理论；真实应力；疲劳安全率

　　Research Analysis and Application of Mechanical Structure Fatigue Strength

　　Zuo Yajun，Li Jinqiang，Cheng Zuyi

　　(Dongguan Shenpeng Electronics Co．，Ltd．，Dongguang，Guangdong 523583，China)

　　Abstract：In the long－term use of most mechanical structure products，some parts will bear various alternating stresses and need to be checked for fatigue strength．In view of the fact that domestic literature has not yet formed a complete standard guidance for fatigue strength calculation and verification，based on the basic theory of fatigue strength，the basic concept of fatigue strength，stress types and application rules of S－N fatigue curve was explained in detail．The relationship between the slope k and the cyclic stress characteristic r in the fatigue limit stress diagram，and the theoretical calculation and application of the four average stress fatigue curves of Goodman，modified Goodman，Goebbels and Soderberg were analyzed and obtained．The meaning of real stress and engineering stress and the difference between them were explained．The checking rules and requirements of fatigue strength were comprehensively analyzed，and the calculation formula for the design fatigue safety rate of infinite life was derived．Based on the research literature at home and abroad，the criteria for determining the fatigue safety rate of infinite life design were given，and an effective theoretical method for calculating the fatigue strength was obtained，which provided an effective and accurate theoretical basis for checking the fatigue strength of mechanical structures．

　　Key words：fatigue strength；Goodman theory；true stress；safety ratio of fatigue

　　0引言

　　疲劳断裂在整个工程结构失效中约占80％左右，造成的损失极大。疲劳断裂在发生之前会伴随大幅度变形，且没有任何前兆。

　　机械结构类的产品在长期使用过程中，部分零部件会承受交变应力，如在旋转电机中：旋转轴承受对称循环应力、转子铁承受脉动循环应力等，因此在强度计算校核时不仅要校核屈服强度，还需考虑疲劳强度的校核，否则可能会造成质量隐患。疲劳强度的校核方法有多种，评判标准也有所不同，且在国内研究文献中研究分析了疲劳强度的理论和实际应用[1－8]，但对疲劳强度安全率的计算理论没有系统地进行详细说明和推导，文献[9]基于非线性累积损伤理论的金属材料疲劳寿命研究，从材料剩余疲劳寿命的角度出发，考虑载荷间相互作用的影响并引入修正参数，基于S－N曲线提出了添加载荷间相互作用效应的非线性累积损伤改进模型。利用3种常见材料的经典疲劳试验数据对新改进的模型进行了验证，并与Miner准则和朱顺鹏模型的预测结果进行对比分析，验证了改进模型的有效性和准确性，但计算过程复杂且很难考虑到其他因素的影响，文献[10]提到了疲劳安全率的基本计算公式，但对该公式没有做理论推导过程，故会造成相关工作者在进行疲劳强度校核时会遇到困难，不能正确判定疲劳强度是否满足要求。

　　针对前面所述的问题，本文较为系统地介绍了疲劳强度基本理论概念，详细说明了疲劳极限应力图中常见的4大平均应力疲劳曲线的理论应用，阐明了疲劳强度的校核规则，推导出相关理论计算公式，为研发工程师及相关的研究人员提供明确的参考指引。

　　1疲劳强度基本概念

　　机械结构疲劳，即在交变应力下，即使应力低于屈服强度或抗拉强度时，材料也会发生断裂失效的现象，其微观解释就是，在足够大的交变应力下，金属晶体首先形成许多微观裂纹，在长时间的交变应力下，这些微观裂纹会出现稳态扩展，随着裂纹的扩展增大，构件截面会逐步削弱，直至断裂失效[11－13]。

　　交变应力即应力值是随时间变化的，并且成周期性。如图1所示，在一个周期内应力的变化过程，称之为一个应力循环，可用以下4个参数来描述：(1)最大循环应力σmax；(2)最小循环应力σmin；(3)平均应力σm＝(σmax＋σmin)／2；(4)应力振幅σr＝(σmax－σmin)／2。

　　不同的交变应力类型用循环特征r＝σmin／σmax来表示，范围通常为－1＜r＜1，r值不同就表示不同的循环应力，常见的应力类型有如下5种：(1)对称循环应力，σmax＝－σmin，r＝－1，如旋转轴类零件等；(2)波动循环应力，σm＞0，σm＞σr，0＜r＜1，如发动机气缸等；(3)脉动循环应力，σm＝σr，σmax或σmin＝0，r＝0，如齿轮、压力容器等；(4)其他不对称交变应力，σm≠0，如发动机连杆等；(5)随机循环应力，应力的大小或方向随时间呈无规律的随机变化，如家用挂车前轴等。静应力可以看成交变应力循环的一种特殊情况，此时应力随时间没有变化，为一个恒定值，应力循环特征r＝1，σr＝0，σm＝σmax＝σmin。

　　此外，对材料进行疲劳寿命试验可以得出S－N曲线，即应力－寿命曲线，如图2所示。

　　S－N曲线把整个平面分成破坏区和非破坏区两部分，平面上的每一个点对应着材料受载的情况(σmax，N)，表示材料受到最大应力为σmax的交变应力循环，且循环次数为N。如果该点落在破坏区，材料将会发生疲劳失效，落在非破坏区就不会发生疲劳破坏；如果材料所受的最大交变应力为σ0，通过S－N曲线就可以求出材料受到N0次循环之后就会发生疲劳失效(如图1中的A点)；当最大应力值小于σw时，材料无论循环次数是多大，点总是落在非破坏区，不会发生疲劳失效，故称σw为材料的疲劳极限。

　　2疲劳极限应力

　　2．1斜率k与循环特征r

　　疲劳极限应力图是以应力振幅σr为纵坐标、平均应力σm为横坐标。平面上的每一个点P(σr，σm)对应一种循环应力特征，这个点P与坐标原点的连线的斜率如下：

　　由此可知，循环应力特征r和斜率k有一对应的关系。如果平面上的两个点分别和原点相连的直线的斜率相等，则它们是相同类型的交变应力，否则是不同类型的交变应力。如图3所示，点A和点B的循环应力特征r相同，属于同类型的交变应力，而点A和点C属于不同类型的交变应力。

　　2．2疲劳极限平均应力理论

　　在疲劳极限应力图中，已知一个点P(σr，σm)，则可以反求出此交变应力的最大应力σmax和最小应力σmin：

　　因此，根据σmax＜σw(疲劳极限)就可以画出对应的疲劳极限临界点，把不同循环特征的疲劳极限值连起来，就是疲劳曲线。另外，落在横轴上的点对应的应力状态是静应力(应力振幅σr＝0)，落在纵轴上的点σ－1对应的是对称循环应力。

　　关于材料的疲劳极限有4种平均应力理论[11－13]，分别如下：

　　式(4)~(7)中：σT为真实应力；σs为屈服应力；σb为抗拉强度；σw为疲劳极限，一般是由试验测定得出，但其与静强度之间存在经验关系算式[14]，如表1所示。

　　4种平均应力理论和试验值之间的曲线如图4所示。从图中可看出试验得出的数据大都位于修正古德曼(Modified Goodman)线和戈倍尔(Gerber)线之间，所以工程上常采用前3种理论曲线的较多，而索德伯格理论(Soderberg)过于保守，在工程中很少被使用。我国一般使用修正古德曼(Modified Goodman)线或戈倍尔(Gerber)线计算校核疲劳强度，而日本等国家普遍使用古德曼(Goodman)线计算校核疲劳强度[16－17]

　　2．3真实应力σT

　　在古德曼理论(Goodman)和国内外的研究文献[11－13，16－17]中会涉及到材料的真破断应力，其指的试件做拉断试验时，拉力除以拉断时的颈缩截面积A1，亦称真实应力。国内少有资料解释该应力含义，我国常用的是工程应力(抗拉强度σb)，即：拉力除以初始截面面积A0，如图5所示。

　　3疲劳强度校核

　　3．1校核规则

　　机械结构的疲劳强度校核一般包含两个方面内容：结构既不能发生疲劳破坏也不能发生塑性变形，因此要求就是交变应力的最大应力要同时小于疲劳强度和屈服强度，即：

　　如图6所示，疲劳破坏线和屈服破坏线把σm－σr平面划分为6个区域，根据交变应力(σm，σr)代表的点所落的区域来评估校核强度是否满足要求，相关判定规则如下：

　　(1)若点(σm，σr)落在1、2、4和6区域，即在疲劳破坏线下方，那么材料不会发生疲劳破坏；

　　(2)若点(σm，σr)落在1、2、3和6区域，即在屈服破坏线下方，那么材料不会发生塑性变形；

　　(3)若点(σm，σr)落在3区域，该区域为疲劳失效区，材料的疲劳破坏发生在塑性变形之前，只需校核疲劳强度即可；

　　(4)若点(σm，σr)落在4区域，该区域为塑性失效区，材料的塑性变形发生在疲劳破坏之前，只需校核屈服强度即可；

　　(5)若点(σm，σr)落在1、2和6区域，材料既不会发生屈服破坏，也不会发生疲劳破坏。

　　3．2疲劳安全率计算

　　由于国内普遍采用修正古德曼理论疲劳线，故在本文中仅推导基于修正古德曼理论的疲劳安全率计算，其他3个平均应力理论的疲劳安全率计算的过程方法与古德曼理论的相同，就不再详细推导计算。

　　如图7所示，已知交变应力的特征(σr，σm)，对应在σr－σm平面上的点A。根据前文2．1节内容可知OA射线上都是同一交变应力特征类型，这样可通过求OA射线和疲劳强度的交点A′，得到该点A′循环特征下的疲劳强度大小，即：A′点横坐标和纵坐标的总和σmax＝σr＋σm。

　　疲劳安全率可定义为交变应力对应的循环特征下的疲劳极限值除以此时的最大应力，即：

　　式中：σ为交变应力对应的疲劳极限值；σmax为最大应力。

　　结合图3示意，设横坐标为x轴，纵坐标为y轴，根据平面解析几何，由直线的截距式可得修正古德曼理论(Modified Goodman)疲劳强度线的方程为：

　　式(13)的疲劳安全率计算公式适用于任何循环特征的交变应力，只要已知材料的对称循环疲劳极限σ－1、抗拉强度σb和长期工况下的最大应力σmax、最小应力σmin，即可算出疲劳安全率。

　　在国外的研究文献中，许用疲劳安全率一般是取1．3[14－16]，即疲劳安全率sf＞1．3时，结构的疲劳强度满足要求。

　　3．3应力特征点区域判定

　　如图6所示，为了确定应力特征点(σr，σm)落在1区域还是2区域，可先求出疲劳强度线和屈服强度的交点B的坐标，联立下面方程：

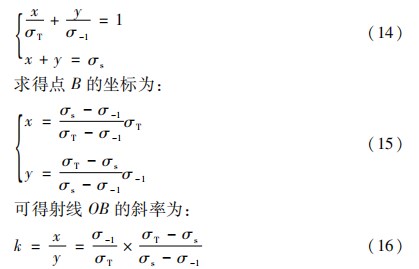
　　若需校核的点A对应的射线OA的斜率σr／σm大于k，则点A就落在区域1内；若射线OA的斜率σr／σm小于k，则点A落在区域2内。

　　3．4疲劳强度判定标准

　　在图2中的S－N曲线是由两条直线组成的折线，按斜线部分进行设计称有限寿命设计，按水平部分进行设计称为无限寿命设计。对于有限寿命设计来说，疲劳损伤累积理论是其重要依据，而对于无限寿命设计，则主要是计算其安全系数，前文3．2节所的疲劳安全率计算是适用于无限寿命设计，理论上当sf≥1．0时，所校核的零件为无限寿命，即永不会发生疲劳断裂，但综合考虑其他因素的影响，疲劳安全率一般取大于1．0。

　　无限寿命设计要求零件在无限长的使用期间内不发生疲劳破坏，用该准则进行设计可能会造成零件结构尺寸相对偏大，但对于长时间运转的零件，它是一个很好的设计准则。

　　如表2所示，针对机械结构零部件疲劳强度校核的许用疲劳安全系数制定原则如下：

　　(1)根据文献查得，对于材料较均匀，载荷及应力较精确时，许用疲劳安全系数建议取1．3，即疲劳安全率大于或等于1．3时，结构的疲劳强度满足要求，永不会发生疲劳失效；

　　(2)在日本的机械行业中[15]，结构件无限寿命设计的许用疲劳安全率一般取大于或等于1．3，即疲劳安全率大于或等于1．3时，其零件的疲劳强度满足要求。

　　4结束语

　　本文基于疲劳强度的基本理论，详细解释了疲劳强度的基本概念、应力类型和S－N疲劳曲线的应用规则，并理论分析计算确定疲劳极限应力图中斜率k与循环应力特征r之间的关系，以及古德曼、修正古德曼、戈倍尔和索德伯格四大平均应力疲劳曲线的理论计算及其应用，诠释了真实应力和工程应力的含义及两者之间的区别，并综合分析疲劳强度的校核规则和要求，结合σm－σr平面区域图，明确了交变应力(σm，σr)代表的点在各区域的校核地要求和规则，并理论推导计算出无限寿命设计疲劳安全率sf的计算公式，适用于任何循环特征的交变应力，只要已知材料的对称循环疲劳极限σ－1、抗拉强度σb和长期工况下的最大应力σmax、最小应力σmin，即可算出疲劳安全率sf。最后结合国内外研究文献给出无限寿命设计的疲劳安全率判定标准及依据，得出了一种有效的疲劳强度计算理论方法，为机械结构的疲劳强度校核提供了一种有效而准确的理论计算依据，对于机械结构零部件的疲劳强度校核计算具有重要的指导价值。

　　参考文献：

　　[1]李莉．机械零件疲劳强度若干问题的研究[D]．沈阳：东北大学，2009．

　　[2]陈震．金属材料缺口件疲劳寿命预测方法研究[D]．秦皇岛：燕山大学，2019．

　　[3]徐友坤，鲁连涛．基于临界距离法的含表面缺陷车轴试样疲劳强度预测[J]．机械强度，2022，44(4)：825－830．

　　[4]何丁妮，廖云飞．不同疲劳加载方法对金属悬臂梁性能影响的试验研究[J]．实验力学，2022，37(3)：430－438．

　　[5]王严，郭城臣，樊浩．基于子模型技术的焊接头疲劳强度评估[J]．机电工程技术，2021，50(2)：51－54．

　　[6]梁旭．金属材料疲劳强度影响因素的研究[D]．沈阳：东北大学，2009．

　　[7]段红燕．一种新型的疲劳强度预测模型[J]．上海交通大学报，2022，56(6)：802－807．

　　[8]刘海军．基于零部件疲劳试验数据的统计分析研究[J]．内燃机，2022，38(1)：33－38．

　　[9]傅振升．基于非线性累积损伤理论的金属材料疲劳寿命研究[D]．济南：山东大学，2022．

　　[10]左亚军．基于ANSYS的电梯轿架强度计算与分析[J]．机电工程技术，2015，44(6)：39－42．

　　[11]Claude Bathias，Andre Pineau．Fatigue of structures and materials[M]．England：Wiley－Iste，2011．

　　[12]Ralph I．Stephens．Metal fatigue in engineering－2 nd Edition[M]．England：Wiley Interscience，2000．

　　[13]Schijve，J．结构与材料的疲劳(第2版)[M]．北京：航空工业出版社，2014．

　　[14]闻邦椿．机械设计手册(第五版)第六卷[M]．北京：机械工业出版社，2010．

　　[15]山田敏郎．金属材料疲劳设计手册[M]．成都：四川科学技术出版社，1988．

　　[16]K Narynbek Ulu，B Huneau．True stress con－trolled fatigue life experiments for elastomers[J]．International Journal of Fatigue，2017(104)：171－182．

　　[17]Ralph I Stephens．Metal fatigue in engineering－2nd Edition[M]．England：Wiley Interscience，2000．