摘要：海上风电机组在整机载荷计算时必须考虑整机与基础的阻尼比。但现有条件下，模态阻尼比的识别精度偏低，工程应用上，模态阻尼比测试值存在离散性，短期测试难以得到有统计意义的结果。为此提出一种针对海上风电机组的阻尼比评估方案，采用运行模态分析(Operational Modal Analysis，OMA)方法对广东沿海某风电场某型号风机进行1个月的持续测试，应用随机子空间法识别阻尼比，确定了阻尼比测试值的概率分布模型，研究了阻尼比离散程度与采样数据时间、测试样本数量、风速、湍流等因素的关系。结果发现随着采样时间的增加，置信区间上下边界均有增大的趋势，阻尼比离散程度在低风速高湍流下较大，随着风速增加而降低。给出阻尼比分布模型与95％置信区间，将阻尼比识别值置信范围降低到0．1％。所提方案降低了测试时间成本，为产品设计研发提供了具备统计意义的实测数据支持。

　　关键词：模态阻尼比；随机子空间法；参数估计；置信区间

　　0引言

　　近年来，我国海上风电快速发展，但海上风电机组的高成本严重制约行业发展[1]。在整机的载荷计算时，必须考虑整机与基础的阻尼比，避免计算结果过度保守，导致成本过高。对于大型结构，一般使用运行模态分析(Operational Modal Analysis，OMA)方法。在大量测试实践中，人们发现对阻尼比的识别精度远低于对频率和振型的识别精度[2]，并且表现出阻尼比离散的特性[3－5]。这导致阻尼比通常很难确定，阻碍了产品设计研发工作。

　　几十年来，人们在理论研究和工程实践中针对阻尼比识别做了大量探索。相关理论研究表明，影响阻尼矩阵的因素十分复杂。文献[4]利用矩阵摄动理论，以粘滞阻尼为假设，对钢梁结构进行EMA试验，对有限元法形成的阻尼矩阵与质量矩阵的相似性进行了分析，指出阻尼作用下弯曲自振频率与仿真值偏小。文献[6]提出一种改进的半功率带宽法，对一个五自由度结构进行仿真，利用尺度－空间峰值拾取法(Spatial Space Peak Picking，SSPP)[7]对频响函数进行峰值拾取，得到峰值矩阵，再转化为单自由度频响函数，利用传统半功率带宽法识别阻尼比。文献[8]对半功率带宽法和内积法进行分析，指出随着采样点数增加，阻尼识别的相对误差有先下降后上升的趋势。

　　实际工程应用中，文献[9]等利用振型频率经验拟合公式，对钢箱梁悬索桥的模态阻尼比进行识别，并指出精确拟合阻尼比结果意义不大，应主要研究其变化趋势。文献[10]等采用前10阶模态的质量参与系数所占百分比作为对应模态阻尼比的附加权重值，加权得到大型冷却塔结构的等效阻尼比拟合公式。文献[11]分析了半功率带宽法估计阻尼比的影响因素，并提出一种INV阻尼计识别法。文献[12]针对大桥阻尼比测试离散的现象，用响应的均方根值结构动力响应振动水平评价指标，指出环境载荷振动水平较低，采样时间较长，会降低识别的阻尼比的离散度。文献[13]花费8个月时间，进行随机子空间法中的非加权主分量算法和主分量算法的对比试验，得到被测试风机的阻尼比在0．1％~1％内波动的结论。由此可见，工程应用场景下，为了得到可靠的阻尼比测试值，需要进行大量测试。而海上风电现场外部条件不可控制，停机时间随机性强，有时候长时间不停机，难以获得有效的测试数据。而申请停机工作相对困难，海上项目运维成本非常高，这些外部因素都会导致测试工作时间的延长，时间成本成为制约测试工作的重要因素。

　　在无法克服这种不利条件的情况下，本文将风机阻尼比视为一个服从某一个未知分布的随机变量，每一次测试是这个随机分布的一组测试样本，这样就把提高阻尼比识别精度问题转化为求随机变量分布形态和参数估计问题。本文提出一种模态阻尼比可信度评价方法，利用概率模型参数估计方法讨论了不同采样时间、样本个数下，阻尼比的合理波动区间及其变化趋势，在有限的测试时间内，得到可靠的统计结果。分析流程如图1所示。

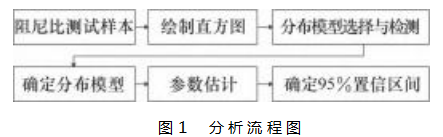
　　鉴于测试的海上基础风机结构属于圆柱体对称结构，内部构造复杂，模态频率具有低频、密频的特性，本次采用随机子空间法进行模态参数识别，其具有较高的效率、密集模态识别精度和抗噪能力[14]，适合工程应用。

　　1随机子空间方法简介

　　结构振动系统可由二阶微分方程表示：

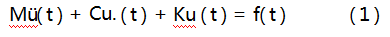
　　式中：M、C、K分别为系统的质量、阻尼、刚度矩阵；ü(t)、u.(t)、u(t)分别表征加速度、速度、位移矩阵；f(t)为激励向量。引入系统状态向量，即

　　可以得到反映振动系统运动状态及表征结构系统与输出间关系的状态空间方程，同时也构建了结构连续时间状态空间模型：

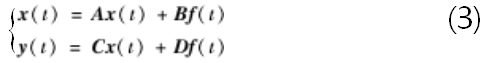
　　式中：A为n×n阶反映系统构成及系统状态变化的系统矩阵；B为n×r阶反映输入与输出向量间关系的传递矩阵；f(t)为r×1输入向量；n为两倍的系统自由度数；r为输入激励个数；m为输出响应个数。由于实测信号数据是离散的，需要将式(3)改为离散状态方程，引入状态变量x(t)的通解：

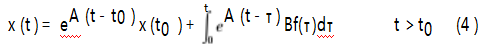
　　设时间隔为Δt，则离散时间序列可以写为0，Δt，2Δt，…，(k＋1)Δt，…，将t＝(k＋1)Δt，t0＝kΔt代入方程(4)，可得：

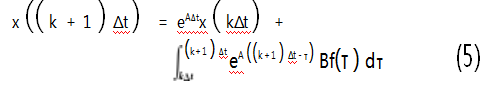
　　设f(t)在采样间隔内为常数，用xk＝x(kΔt)和xk＋1分别表示由k和k＋1时刻的位移和速度向量组成的系统状态向量。经整理式(3)可以写为动力学系统离散的状态空间方程：

　　式中：xk为离散的状态空间向量；yk为测量响应；A r为离散的系统矩阵；Br为离散的输入矩阵；Cr为离散的输出矩阵；Dr为离散的传递矩阵。

　　考虑测试系统的不确定性，将随机分量以过程噪声wk与测量噪声vk形式加入原式中，则有：

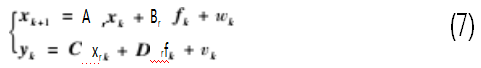
　　如假设未知随机项wk，vk和输入项fk均具有零期望值的白噪声特性，则原式可写成纯随机输入的离散状态方程：

　　式(8)即为随机子空间法的基础方程，其中Ar和Cr分别为n×n阶的状态矩阵和m×n阶的输出矩阵。系统的动力特征由特征矩阵Ar的特征值和特征向量表示。

　　基于实测数据建立Hankel矩阵。假设结构有m个测点，各个测点实测数据长度为j。将测点响应数据按照式(9)形式组成2mi×j的Hankel矩阵，它包含2i块和j列，每块有m行。将Hankel矩阵的行空间分成“过去”和“将来”行空间，可以写成：

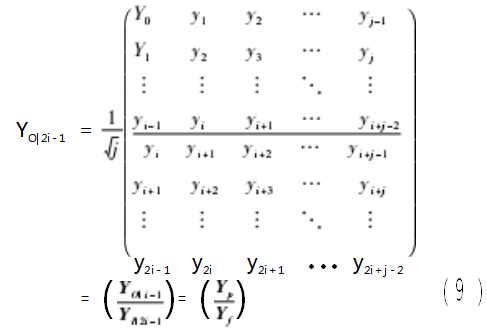
　　式中：yi为第i时刻所有测点的响应；YO|i－1和YI|2i－1分别表示Hankel矩阵中前后i块所有测点数据组成的矩阵；YP和Yf分别表示矩阵的“过去”和“未来”行空间。由于实际测试数据组成Hankel矩阵列数j较大，需要对Hankel矩阵进行QR分解：

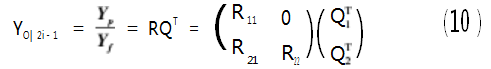
　　由空间投影性质，可得出行空间的正交投影：

　　式中(·)＋表示伪逆。对正交投影进行分解，表示成可观矩阵Oi及状态向量的卡尔曼滤波估计Xi形式，同时进行奇异值分解，可得到系统矩阵A和C：

　　得到系统的状态矩阵和输出矩阵后，模态参数识别转化为特征值分解问题，对系统状态矩阵进行特征值分解：

　　式中：Λ为离散事件系统的特征值；Ψ为A的特征向量。根据离散时间系统与连续时间系统的特征值关系，模态阻尼比ξi可表示为：

　　式中Re表示复数的实部；·表示复数的模。

　　2工程测试实例

　　2．1机组现场与测试方案

　　为了评估单桩机组基础设计的经济性，需要对整机的第一阶模态阻尼进行测试。以广东沿海某风场某型风机作为测试对象，如图2所示，频率和阻尼设计参考值分别为0．262 Hz和0．6％~0．7％。对其进行连续1个月的测试。测试设备包括北京某振动噪声技术研究所的INV3068WP系列动态数据采集仪和DASP分析软件，传感器为某地震工程研究所研制的941B－H低频拾振器，如图3所示。采集器采样频率为25．6 Hz，24个采集通道，每一个测试组采样时间为60 min。与此同时，从风机主控同步采集风速、风向、功率、偏航角度等机组信号，用来后期对数据进行分析。

　　在塔筒的第2节塔筒上端法兰处、第3节塔筒上端法兰处、偏航平台处，将塔筒四等分布置4个测点，每个测点分别沿着塔筒的径向和切向布置两个拾振器，共布置24个拾振器。

　　本次试验按照塔筒0°、90°、180°、270°的径向和切向布置测点，总共3台INV3068WP－P1采集仪，每台采集仪8通道，采用941B－H拾振器对塔筒的振动速度进行数据采集，测试几何模型如图4所示。

　　2．2初步测试结果

　　观察测试结果发现，本次测试主要体现了塔筒的第一阶“前后一弯”模态，如图5所示。本文仅讨论“前后一弯”模态的阻尼比的评估方法。

　　筛选停机工况数据，应用随机子空间法得到41组1小时测试数据，结果如表1—2所示。

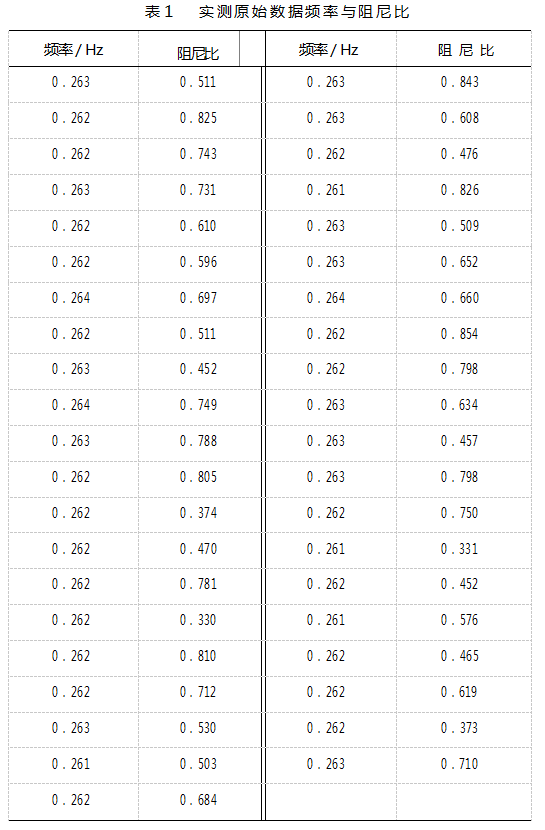
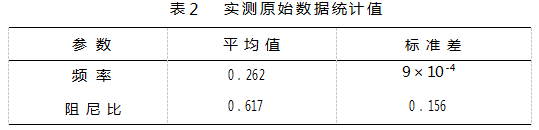
　　从表2中可以发现，频率的识别结果非常稳定，集中在0．262~0．264 Hz，但是阻尼比的识别结果比较离散，数值在0．3％~0．8％之间都有出现。图6展示所有数据的阻尼比数据量密度直方图。观察直方图可知阻尼比数据量过少，统计意义不强。因此需要对测试数据进行时间段分割，获取更多有效停机数据进一步分析，以增强数据的统计意义。

　　2．3数据分割与分布模型的选择

　　将测试期间数据分别按照每组10、20、30、40 min分割，图7为10 min阻尼比概率密度分布图。表3为不同采样时间的数据量。

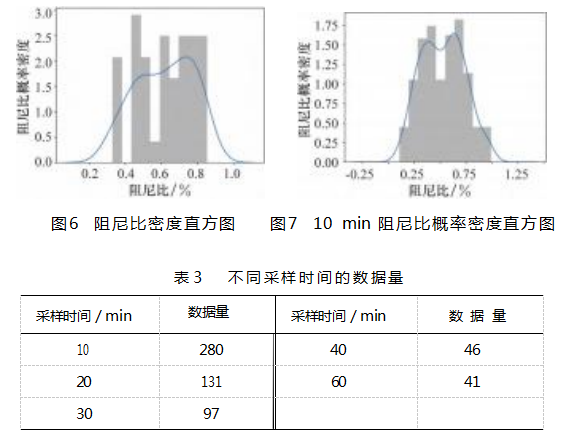
　　观察图7可见，阻尼比的分布形态为两侧低中间高，对以下5种分布模型进行Kolmogorov－Smirnov(KS)检验，设定显著性水平p为0．05，分布拟合效果如表4所示。

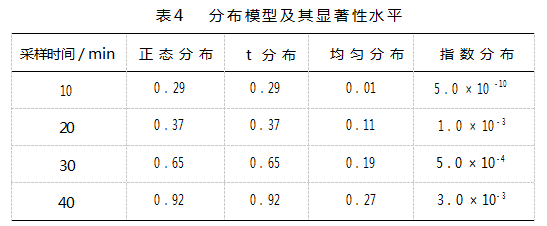
　　由表4展现的信息，只有正态分布和t分布模型的p值均大于0．05。因此可认为阻尼比近似服从正态分布模型。一般情况下，如果样本数量大于30，则选用正态分布模型，否则选用t分布模型，这里选用正态分布模型。

　　2．4阻尼比置信区间与采样时间的关系

　　为了展示阻尼比分布在全局上的趋势，采用核密度估计方法绘制分布图。核密度估计方法是一种非参数概率密度估计方法，其优势是不依赖于先验概率分布模型，直接利用样本数据估计数据分布特征，避免了先验模型拟合结果严重偏离实际分布[15]。为避免局部微小特征对全局趋势的影响，核密度估计可设置较大的带宽参数[16]。图8展示不同采样时间下阻尼比分布趋势，竖线为置信区间上下界，数值在表5中体现。

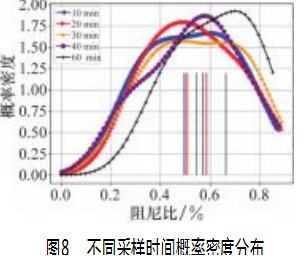
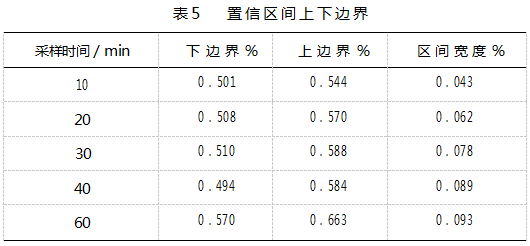
　　阻尼比的概率密度分布，近似呈现正态分布样式，95％置信区间稳定在0．5％~0．7％内。随着采样时间的提高，数据量相应的变少，区间上下界有向右移动增大的趋势。

　　2．5样本个数与置信区间宽度的关系

　　样本越多，越能反映总体情况，置信区间宽度就会越小。如图9所示，不同数据组的置信区间宽度与样本数据量变化趋势接近[17]。样本数据量达到50，数据组的置信区间的宽度可降低至0．1％附近，要求测试组数要达到50组以上才能确保结果具有比较可靠的统计意义。

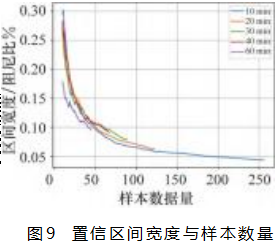
　　需要指出的是，短采样时间识别的阻尼比的数据量会很多，但不意味着为了提高样本数量就可以任意缩短采样时间。相关工程经验指出，对于大型结构，采样时间过短可能会出现未能有效激发出某些阶模态，导致稳定图变差，模态参数识别的不确定度增大[18]。本次测试只关心第一阶模态阻尼，因此，在满足测试可靠度和样本数量的综合权衡下，阻尼比置信区间可以按采样时间20~30 min的结果作为结论。

　　2．6阻尼比离散程度与风速、湍流的关系

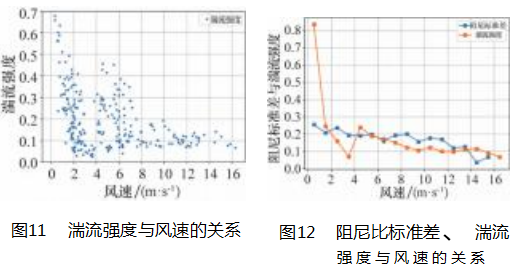
　　根据文献[19]的研究成果，风电机组的总阻尼主要包括结构阻尼和气动阻尼，大风速下，风速风向相对稳定，作用于机组的气动载荷相对稳定，使气动阻尼也相对稳定，而小风速下，风速风向变化剧烈，湍流强度较高，导致气动阻尼变化较大，使得低风速环境下阻尼比更加离散。图10为10 min间隔下阻尼比与风速的关系，发现阻尼比的离散程度随着风速增加而降低，并向中间值趋近。图11显示湍流强度与风速的关系，图12显示了在每个1 m／s的风速段内，阻尼比的离散程度随着风速提高逐渐下降，与湍流强度随风速的变化趋势接近。

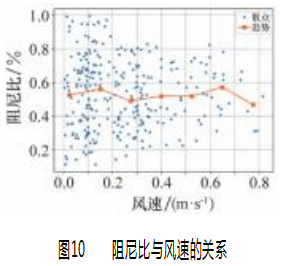
　　3结束语

　　本文对海上某型风机进行了1个月持续测试，针对阻尼比离散的现象，分析了模态阻尼比与采样点数、样本数据量的关系，归纳出了阻尼比分布的分布模型和置信区间，为产品设计研发提供了实测数据支持，形成以下结论。

　　(1)本次测试的海上风电机组阻尼比分布近似呈正态分布，95％置信水平下的置信区间为0．5％~0．7％，与设计参考值0．6％~0．7％接近，可以验证本次测试结果的正确性，并且机组在停机工况下，阻尼比均值在这个范围内波动在绝大多数时间内是正确可信的。

　　(2)用样本估计总体时，随着测试样本数据量的增加，置信区间宽度会逐渐降低。测试样本数据量要至少到50组以上，才能得到比较稳定的有统计意义的结果，置信区间宽度可降低至0．1％以内。

　　(3)随着采样时间的提高，阻尼比的直径上下边界均有增大的趋势。

　　(5)机组在不同风速段下受到的载荷不同，在低风速段，湍流较高，阻尼比识别离散较严重，而在高风速段，湍流较低，阻尼比离散度相对较小。

　　(6)对于工程应用，阻尼比的识别需要进行大量测试以得到具备统计意义的结果。海上风力发电机组停机时间较少，本文通过数据切割，提高测试组数的方法，提高了统计数据量，以30 min数据样本为参考，同等数据量的前提下，将测试工作周期降低了二分之一。

　　参考文献：

　　[1]金长营．海上风电项目全寿命周期的成本构成及其敏感性分析[J]．太阳能，2022(3)：7．

　　[2]TORVIK P J．On estimating system damping from frequency response bandwidths[J]．Journal of Sound and Vibration，2011，330(25)：6088－6097．

　　[3]徐志伟．海上风电升压站平台设计及有限元计算分析[J]．内蒙古电力技术，2022，40(1)：44－48．

　　[4]刘新明．矩阵摄动方法在阻尼系统动力学问题中的应用[D]．大连：大连交通大学，2017．

　　[5]HE Xianfei，MOAVENI B，CONTE J P，et al．System identification of Alfred Zampa memorial bridge using dynamic field test data[J]．Journal of Structural Engineering，2009，135(1)：54－66．

　　[6]杨昆茂．基于改进半功率带宽法的结构阻尼比识别理论研究[D]．大连：大连理工大学，2021．

　　[7]顾红．基于频域的结构密集模态自动识别方法研究[D]．大连：大连理工大学

　　[8]程惠．采样时间长度对阻尼识别影响的研究[D]．镇江：江苏大学，2017．

　　[9]杨舒蔚，葛容华．钢箱梁悬索桥模态阻尼比分析[J]．四川建筑，2018，38(2)：159－162．

　　[10]柯世堂，余玮，朱鹏，等．环境激励下冷却塔结构模态测试与阻尼比特性研究[J]．振动工程学报，2020，33(1)：35－46．

　　[11]应怀樵，刘进明，沈松．半功率带宽法与INV阻尼计法求阻尼比的研究[J]．噪声与振动控制，2006(2)：4－6．

　　[12]秦世强，康俊涛，孔凡．桥梁工作模态分析中阻尼比识别的离散性研究[J]．振动．测试与诊断，2016，36(1)：42－48．

　　[13]黄竹也，苗亚超，赵艳，等．基于随机子空间法的风机模态参数识别[J]．科技通报，2017，33(4)：76－78．

　　[14]武耀庭．环境激励下的桥梁结构模态参数识别[D]．北京：北京交通大学，2015．

　　[15]李文栋．风功率预测误差的非参数核密度估计方法研究[D]．保定：华北电力大学，2021．

　　[16]赵李志．基于Copula理论的多部件系统剩余寿命核密度预测方法研究[D]．太原：太原科技大学，2021．

　　[17]丁敏，吴敏，安剑奇，等．基于非参数核密度估计的风电功率预测的方法：CN106548253A[P]．2017．

　　[18]黄鑫，苏亮．加速度采样时长对贝叶斯模态识别的影响探究[J]．低温建筑技术，2020，42(2)：66－71．

　　[19]赵艳．风机结构振动监测及动力响应研究[D]．杭州：浙江大学，2018．