摘要：针对传统的永磁同步电机(PMSM)矢量控制安装位置传感器会降低控制系统的安全性和稳定性的问题，提出一种改进的模型参考自适应系统(MRAS)用来估计高速电机的转子速度和位置，实现高速电机无位置传感器的矢量控制。首先基于Popov超稳定性理论选取系统的电流参考模型和电流可调模型，并推导出估计转速的自适应律。然后针对带有模型参考自适应的矢量控制系统具有较大的计算延时问题，提出一种系统模型延时补偿策略。最后，通过Simulink对提出的转速估计系统建立了模型仿真。仿真结果表明，系统稳定运行10 kr/min时转速误差小于±20 r/min，位置误差小于±0.1 rad，在补偿前后相电流减低8.4%，提出的改进模型参考自适应控制系统能够准确地估计高速电机的转子速度和位置。

　　关键词：高速永磁同步电机；矢量控制；模型参考自适应系统；系统模型延时补偿

　　0引言

　　自永磁同步电机(PMSM)出现以来，其控制方法经历了很大的发展。20世纪70年代由德国工程师F Blaschke针对感应电机提出了磁场定向控制[1]。磁场定向控制是通过坐标变换实现转矩分量与励磁分量的解耦控制，Park变换得到的直轴分量为励磁分量，交轴分量为转矩分量[2]。在传统的PMSM控制系统中，大多数安装有位置传感器，比如光电编码器、旋变传感器等，由于这些传感器会受温度、光线、工作环境的恶劣程度以及工作寿命的限制，影响系统的可靠性和安全性，并且传感器的安装和外接线缆都提升了系统成本。为了提升永磁同步电机的系统安全性，国内外的学者先后提出了很多无位置速度传感器的控制算法，这些算法大部分是基于永磁同步电机的数学模型，估算出电机的实时转速和转子位置[3]。

　　目前常用的高速PMSM无位置控制方法主要有滑模观测器、扩展卡尔曼滤波器和模型参考自适应系统(Model Reference Adaptive System,MRAS)[5]。其中滑模观测器有较好的鲁棒性，但是滑模观测器存在固有抖振以及低通滤波器会引起的相位滞后影响转子位置观测的精度。扩展卡尔曼滤波器存在复杂的导数，需要计算雅可比矩阵，需要很高的计算成本，并且扩展卡尔曼滤波器不适用于不连续的系统。模型参考自适应系统不存在固有抖动，计算成本低[6]。

　　综上所述，针对高速永磁同步电机的无位置传感器的矢量控制，本文提出了基于Popov超稳定性理论的具有系统模型延时补偿的模型参考自适应系统。首先基于MRAS原理和PMSM数学表达式选取系统参考模型和可调模型，然后基于Popov超稳定性理论推导出观测电机转速和位置的自适应数学表达式，另外考虑到系统模型的计算延时，提出了一种延时补偿策略，最后基于Simu⁃link搭建了控制系统的仿真模型，对提出的具有系统模型延时补偿的MRAS控制系统进行了验证。

　　1永磁同步电机模型参考自适应系统

　　模型参考自适应转速和位置估计系统主要包含3部分：以电机数学方程式作为参考模型、带有转速未知量的可调模型和用于估算转速和位置的自适应律。参考模型的选取一般是选择已知的电机模型，常见的参考模型有电机电压方程变换得到的电流方程或磁链方程两种；系统的可调模型一般是选择含有转速、位置或磁链信息的数学方程，由于需要将参考模型与数学模型的输出量做差，因此应保证两个模型的输入量和输出量分别对应；根据Popov超稳定性理论，估计可调模型中未知参数，当可调模型在自适应律的调节下与参考模型的完全匹配，即可得到待估计参数。模型参考自适应估计系统的结构框图如图1所示。

　　MRAS系统的自适应律的选取要基于控制工程的稳定性理论，本文综合参考其他学者的研究成果和结论证明，选取相对可靠的Popov超稳定性理论[9]。

　　1.1参考模型与可调模型

　　1.2自适应律

　　自适应律的选择是保证系统稳定的前提条件，基于Popov超稳定性理论推导模型参考自适应系统的自适应律可有效使含有待估计参数的可调模型趋近于参考模型。将永磁同步电机旋转坐标系下的电流方程与选取的可调模型做差，可得：

　　2系统模型延时补偿

　　永磁同步电机无位置传感器矢量控制系统主要包括外环转速环和内环转矩环，转速环一般采用PI控制器或滑模变结构控制器调节，电流环的输出经过Park逆变换输入到SVPWM模块。SVPWM模块更新PWM占空比后控制三相逆变器的开关次序，以控制电机正常转动。系统各模块连接如图2所示。

　　由上述可知，MRAS估算转子速度和位置需要电压和电流作为输入量，处理器从检测电流和电压到更新PWM需要执行大量的运算，包括电流、电压滤波，母线电压纹波处理，Clarke变换，Park变换，MRAS转子速度和位置估计，速度环，电流环以及Park逆变换以及SVPWM模块到最后更新PWM，若高速下还会有弱磁处理和死区补偿以及参数在线辨识模块，因此用检测的电流估计转子位置必然滞后于更新PWM时的实际位置，会引起永磁同步电机在额定功率下达不到额定转速，在额定转速下，实际功率大于额定功率，电机温度升高等影响。

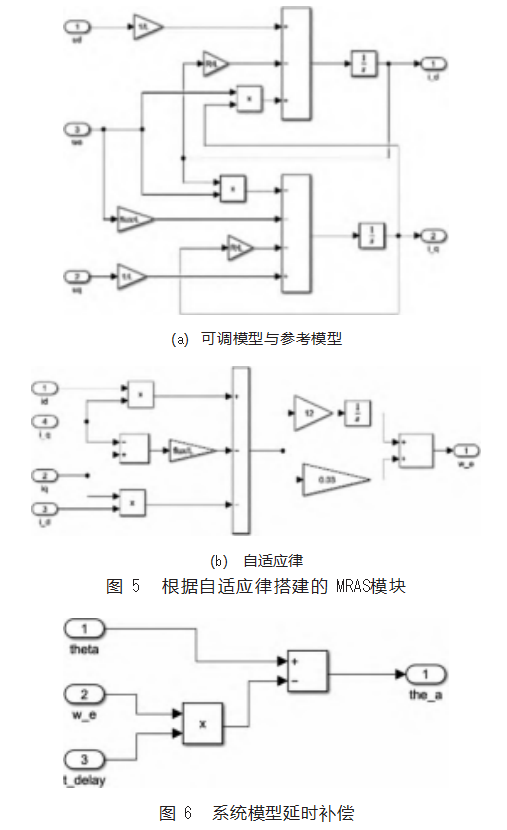
　　针对上述系统模型延时，本文提出一种延时补偿策略，其基本思想是利用计时器准确计时从电流采样到更新PWM所需时间，再根据MRAS估算出的转子速度计算出延时期间转子位置的平均滞后角度，将滞后角度补偿给MRAS估算出的转子位置。

　　补偿角度计算方法如下：

　　式中：θoffset为补偿角度；ω.e为MRAS估算转子速度；tdelay为系统延时时间。

　　更新PWM时转子实际位置θ为：

　　若忽略死区引起的功率不足以及其他延时因素，系统转子位置的理想作用力和实际作用力如图3所示。

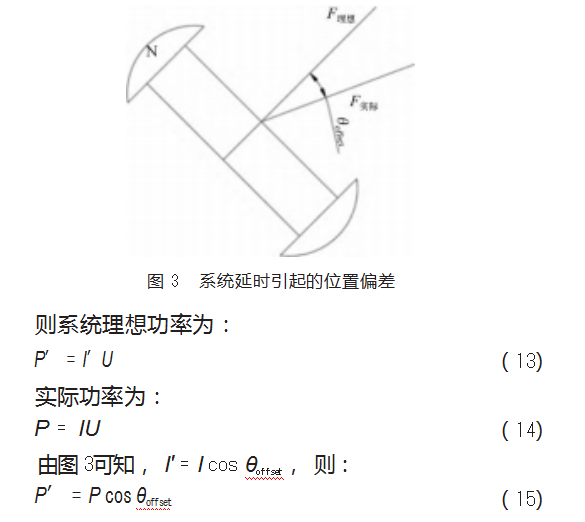
　　因此，额定转速下，系统模型延时会引起功率增大，补偿角度θoffset，即可有效消除由系统延时引起的功率过大或达不到额定转速等影响。

　　3模型参考自适应系统仿真搭建

　　仿真电机采用表贴式永磁同步电机，因此可使励磁电流目标为零，即id=0，转速和位置估算采用具有延时补偿功能的MRAS进行估算。电机基本参数如表1所示。系统采用连续时间仿真，载波频率设为10 kHz，忽略逆变器死区时间。

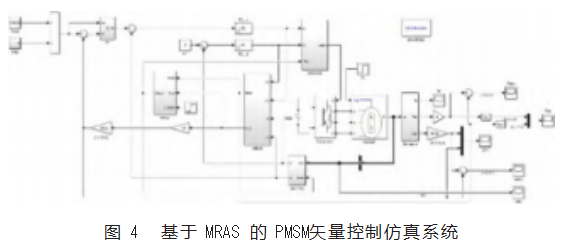
　　根据系统整体结构框图(图2)搭建Simulink仿真系统如图4，仿真系统中MRAS模块则是根据自适应律方程式和方程式搭建，模型如图5所示，延时补偿模块则是根据延时补偿算法方程式和方程式搭建，模型如图6所示，其中延时参数t_delay是参照NXP芯片S12ZVML，在10 kHz的载波频率下从电流检测到PWM更新，包括MRAS模块执行时间的总时间，约为84µs，由于10 kHz的周期为100µs，能够满足测试要求，此外，为了仿真效果，转速环PI参数设置偏小，使速度响应较慢，便于观察。

　　4仿真结果和分析

　　在不考虑系统模型延时的前提下，控制系统给定10 kr/min目标转速，空载启动，在1.5 s加载1 N⋅m负载，在3 s降低目标转速为8 kr/min，在5 s增加目标转速为12 kr/min，可得到仿真结果，如图7~10所示。

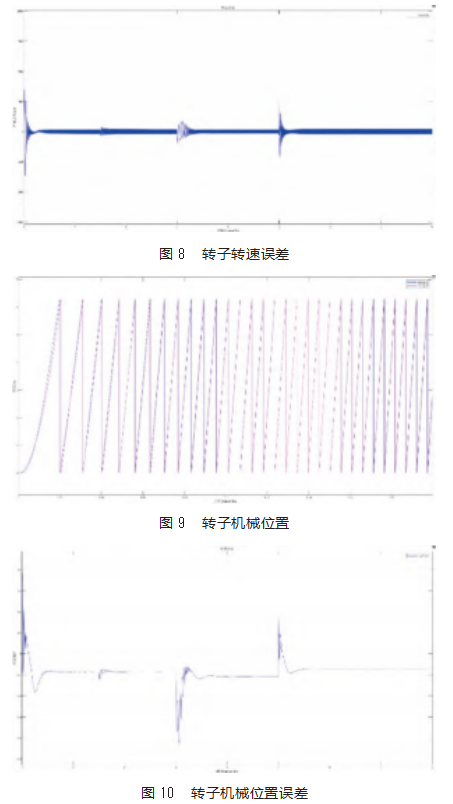
　　由仿真结果可知，在空载时，模型参考自适应系统能够快速跟随调节可调模型，估算出转子转速和位置。在1.5 s外加1 N·m后，转速短暂降低，能够在10 ms内快速上升到目标转速，转子位置有短暂的波动，能够快速平稳运行，相位偏差小于±0.1 rad。随后的减速和加速操作中，模型参考自适应系统均能快速响应，使转速跟随转子实际速度，转速误差小于±20 r/min。综上所述，本文设计的模型参考自适应系统能够在永磁同步电机无位置传感器控制系统中准确识别出电机转子速度和位置。

　　为了进一步验证MRAS与系统延时补偿的效果，在3 s时将系统模型延时补偿模块加入仿真系统，仿真结果如图11~12所示。此外，由于使用连续系统仿真，仿真系统默认无延时，因此，MRAS估算的转子位置减去系统模型延时计算的转子位置误差为带有延时的控制效果，此处延时时间为84µs，10 kr/min下转子延时理论电角度为20.16°。

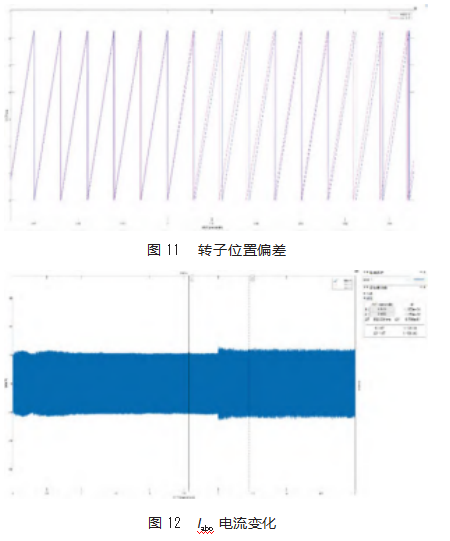
　　由仿真结果可知，在施加延迟前后，转子位置和电流有明显变化，将I=11.50 A和θoffset=20.16°代入式I'=I cosθoffset，可得无延时系统的电流应该为I′=10.79 A，实际相电流下降了8.4%，在可接受范围内符合理论值，有效验证了本文提出的含有MRAS和系统延时补偿模块的永磁同步电机高速无感控制算法的稳定性和可行性。

　　5结束语

　　本文基于永磁同步电机矢量控制系统的基础上，对基于模型参考自适应系统的无位置传感器高速控制方法进行了研究。将永磁同步电机数学模型作为参考模型，建立了基于旋转坐标系的数学可调模型，并基于Popov超稳定性理论，利用参考模型与可调模型均含有相同物理意义的输出量构造一种参考自适应律来辨识电机转子速度和位置信息。考虑到实际处理器在系统模型计算时存在延时，从采集电流到更新PWM不同的处理器和不同的模型具有不同的误差，本文提出了一种针对系统模型延时的补偿方法，并基于NXP的S12ZVML处理器在处理上述系统模型时的延时时间为例设计了Simulink仿真模型，通过在空载、带载以及增加系统模型延时的仿真结果有效的验证了本文提出具有系统延时补偿的MRAS无位置传感器控制系统的可靠性。结果表明，本文提出的具有系统延时补偿的MRAS控制系统具有良好的动态响应和稳态响应，具有较高精度的转速跟随，在10 kr/min下转速误差小于±20 r/min，相位误差小于±0.1 rad，延时补偿模块具有良好的效果，使相电流减小8.4%，减少电机发烫，提升电机使用寿命。因此，本文研究的方案在高速电机无位置传感器矢量控制领域中具有一定的参考价值。

　　参考文献：

　　[1]朱军,韩利利,汪旭东.永磁同步电机无位置传感器控制现状与发展趋势[J].微电机,2013,46(9):11-16.

　　[2]Zheng D K,Zhou Y S,Li H Y,et al.Design of sensorless perma⁃nent magnet synchronous motor controller based on EKF[J].Mi⁃cromotors 2018,51(1):29-33.

　　[3]刘计龙,肖飞,沈洋,等.永磁同步电机无位置传感器控制技术研究综述[J].电工技术学报,2017,32(16):76-88.

　　[4]Xiaojun Liu,Guangming Zhang,Lei Mei.Speed Estimation with Parameters Identification of PMSM Based on MRAS[J].Journal of Control,Automation and Electrical Systems,2016,27(5).

　　[5]孙源,张元良,程绍珲.车载空调压缩机全速度无传感控制策略研究[J].机电工程技术,2021,50(7):105-107.

　　[6]Lin M,Li Y H,Wu C,et al.Predictive Control of Permanent Mag⁃net Synchronous Motor Based on Sliding Mode Model Reference Adaptive System Observer[J].Transactions of China Electrotech⁃nical Society,2017,32(6):156-163.

　　[7]Shweta Singh,Amar Nath Tiwari,S N Singh.Performance evalua⁃tion of MRAS and SMO based sensorless PMSM drives[J].World Journal of Engineering,2020,17(3).

　　[8]Yue Zhao,Chun Wei,Zhe Zhang.A Review on Position/Speed Sensorless Control for Permanent Magnet Synchronous Machine Based Wind Energy Conversion Systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2013(4).

　　[9]苗敬利,李星,董博.基于模型参考自适应的永磁同步电机矢量控制策略[J].机械工程与自动化,2020(6):16-18.

　　[10]何延昭,王贞艳,王金霞,等.高速永磁同步电机模型参考自适应转速观测[J].电气传动,2020,50(10):16-22.

　　[11]唐一文.基于模型参考自适应的永磁同步电机无位置传感器控制[D].株洲:湖南工业大学,2020.

　　[12]李梦瑶,孙逢春,何洪文.基于模型参考自适应的永磁同步电机矢量控制[J].测试技术学报,2019,33(4):322-328.

　　[13]朱瑞杰.基于模型参考自适应的永磁同步电机无位置传感器控制[D].北京:北京交通大学,2018.