摘要：针对结构件在仿真优化过程中参数的主次作用不明确和参数之间的交互作用贡献率大小问题，以拉板结构参数为研究对象，采用均匀设计方法对拉板结构的7个参数(尺寸圆柱外径D、侧板厚度T、肋板厚度B、减重孔长度L、减重孔宽度E、减重孔圆角C和侧板宽度F)进行U2(1210)静力强度试验的仿真模拟和回归分析。结果表明：侧板厚度T与肋板厚度B的交互作用对拉板最大应力值和重量影响最大，R贡献率为51.64%。拉板优化后的模型比拉板优化前的模型最大应力值增大了1.48%，重量减少了35.17%。该研究为拉板多目标结构优化设计提供理论依据。

　　关键词：拉板；结构优化；静力分析；均匀设计；回归分析

　　0引言

　　拉板是机械传动中常用的一种部件，它通过两端的通孔圆柱结构连接主动轴和从动轴，与弯臂等配合可以改变拉力的角度。在矿山机械应用领域，由于作业负载较大，拉板的结构设计往往比较笨重，一方面浪费了材料，另一方面也不利于装配和维修作业。目前，机械结构在概念设计阶段已普遍采用有限元仿真进行模拟和分析。任永强[1]利用ANSYS Workbench的拓扑优化模块对卡簧压装机机架进行了优化设计。郑玉巧[2]以塔架塔顶与机舱底座连接处为研究对象，采用均匀设计法对连接处两要素(厚度、高度)进行的U(92)静强度试验设计并进行数值仿真模拟。减小了塔架应力值和最大位移值，减少了塔架重量。何鹏[3]采取均匀试验设计，对小管径涡流管制冷性能影响很大的结构变量因子，利用CFD软件进行了结构优化计算，并对计算结果进行了回归分析，拟合并验证了经验公式，通过对经验公式寻优，得到了优化后的结构参数。张荣锋[4]利用CFD仿真工具，搭建多芯片共用散热器的热仿真分析模型，确定不同方案的芯片结点温升，最终降低了芯片结点温升。Student P[5]采用ANSYS Workbench对飞机起落架杠杆臂通过响应面模块进行优化，同时利用nCode模块进行了寿命评估，使飞机起落架杠杆臂性能在寿命方面得到改善。

　　从以往的研究可以看出[6-9]，结构参数的研究主要是针对研究对象性能、重量等特性的影响，在参数的主次作用方面并不明确，对参数之间的交互作用也研究较少。因此本文采用UG软件建立拉板三维数模，利用ANSYS Workbench进行静力分析，将拉板结构尺寸作为设计变量，以应力值和重量为优化目标[10]，通过均匀设计方案和回归分析，找出影响拉板性能的显著性参数，并建立回归方程，最终通过仿真实验验证优化结果，为拉板的多目标优化提供了理论依据[11]。

　　1建立拉板三维模型

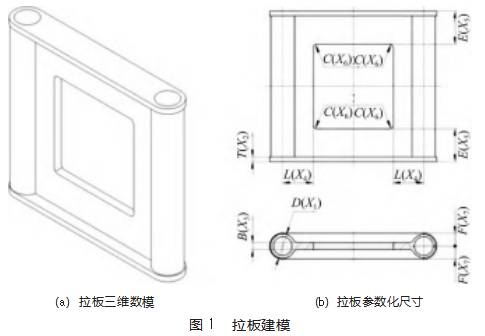
　　采用UG软件建立拉板初始的三维模型，如图1所示。在需要优化的尺寸参数前添加“DS_”[12-13]即能被ANSYS Workbench软件识别，在UG软件中关联打开AN⁃SYS Workbench，此时ANSYS Workbench能识别UG传来的参数化数模，同时也能回传数据给UG，使UG数模实时更新。

　　2有限元分析

　　2.1建立拉板的有限元模型

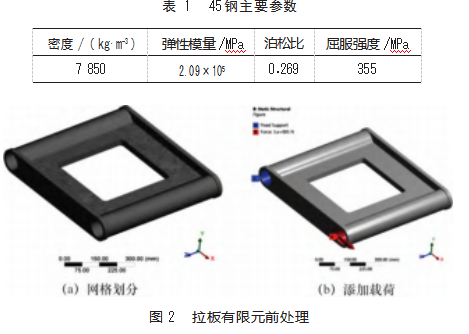
　　在ANSYS Workbench中选择Static Structural静力分析模块，连接UG关联到ANSYS Workbench的模型来完成拉板模型导入。设置拉板材料为45钢，材料参数如表1所示。网格采用四面体方法进行划分，网格单元487 369个，节点732 828个，如图2(a)所示。在拉板一端内圆添加固定约束，另一端内圆添加载荷5×105 N，如图2(b)所示。

　　2.2拉板静力学分析

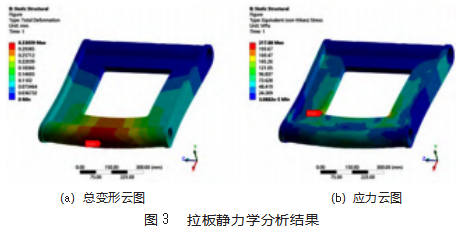
　　图3所示为拉板静力分析后的总变形云图和应力云图，从图中可以看出拉板总变形集中在前端中心区域，最大变形量为0.330 59 mm。拉板最大应力集中在减重矩形区域的圆角处，为217.88 MPa。由于最大应力值未超过材料屈服强度355 MPa，因此拉板最大变形0.330 59 mm在施加载荷结束后拉板的尺寸可恢复原状。另外从图3(b)可以看出，除了减重矩形区域的圆角处应力值较大外，其他区域的应力值云图大约都在100 MPa以下，远小于材料屈服强度355 MPa，说明拉板结构参数有较大的优化空间。

　　3均匀设计方案

　　均匀试验设计法具有试验次数少、试验点“均匀散布”、可用回归分析方法建立模型等优点[14]，避免了有限元软件在处理复杂结构优化时发生庞大的计算量，为处理复杂结构优化问题提供了解决方案。将均匀试验优化法引用到拉板设计中，可优化拉板结构，降低拉板最大应力值并寻求拉板的最佳材料使用量[15]。其主要方法是对拉板进行结构优化设计(尺寸参数优化)，确定各相关尺寸因素的最佳参数组合，综合考虑拉板的最大应力值和重量的权重。

　　3.1拉板均匀试验安排及试验结果

　　拉板原始尺寸圆柱外径D(X1)=100 mm、侧板厚度T(X2)=20 mm、肋板厚度B(X3)=30 mm、减重孔长度L(X4)=130 mm、减重孔宽度E(X5)=140 mm、减重孔圆角C(X6)=15 mm、侧板宽度F(X7)=55 mm、圆柱内径为80 mm、两圆柱孔间距为600 mm。

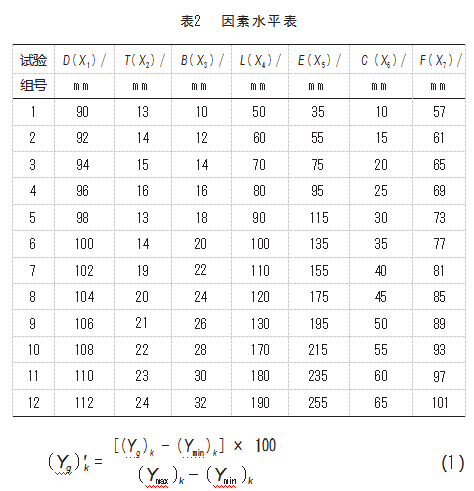
　　考虑到拉板圆柱内径和两圆柱的孔间距为安装尺寸，因此不对其进行参数设定，选取其余尺寸作为研究对象，进行7因素(尺寸圆柱外径D(X1)、侧板厚度T(X2)、肋板厚度B(X3)、减重孔长度L(X4)、减重孔宽度E(X5)、减重孔圆角C(X6)和侧板宽度F(X7))12水平的U 2(1210)试验安排，如表2所示。

　　利用有限元仿真软件按照表3所示的试验方案进行模拟仿真试验，考察不同因素及不同水平下拉板最大应力值σ(MPa)和质量M(kg)，试验方案设计及结果如表3所示。由于拉板最大应力值σ(MPa)和拉板质量M(kg)属于不同量纲指标，无法判断因为试验因数水平变化而引起的拉板最大应力值和拉板重量变化，故采用极值法无纲量化处理。极值法无纲量化公式[16]为：

　　式中：()k为第g号试验k项试验指标观测值；()k为第k项试验指标中最大值；()k为第k项试验指标中最小值；()′k为第g号试验k项试验指标的评分值。

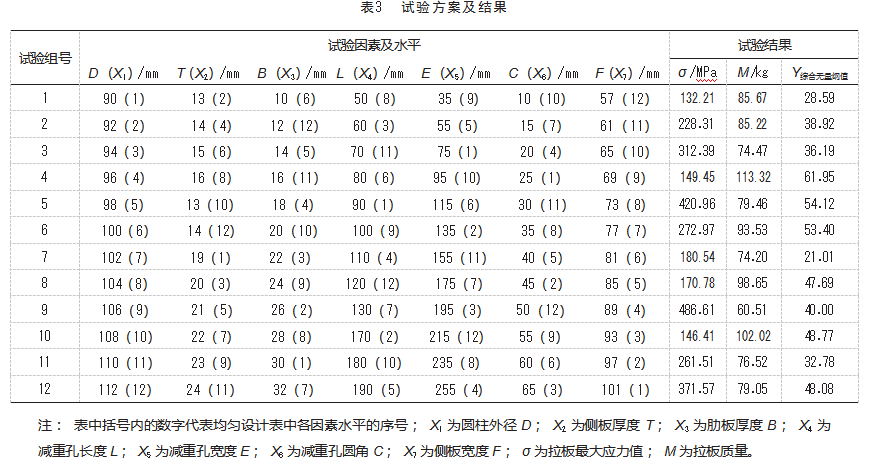
　　由于拉板最大应力值σ和拉板质量M越小越好，因此无需对其无量纲化值进行望大或望小处理，另外赋予拉板最大应力值和拉板重量权重分别为0.4和0.6。拉板最大应力值σ和拉板质量M综合无量纲值公式为：

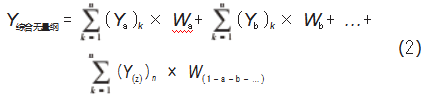
　　式中：Y综合无量纲为拉板最大应力值σ(MPa)和拉板质量M(kg)的综合无量纲值；()k为第k项试验结果指标a的无量纲值，(Yb)k、…、()k与此同理，按a、b、…、z、…字母顺序依次类推；为a指标对应的权重，Wb、…、W(1-a-b…)与此同理。

　　3.2试验数据的回归分析

　　采用回归分析软件对表3中试验数据进行分析，其线性回归方程以及7个因子均不显著，另外通过残差诊断可知7个因子拟合值散点图有“弯曲”和“喇叭口”[17]，故考虑增加“正交多项式”等方式重新进行回归。由于X7与其他X高度相关，因此从方程中剔除，其回归方程为：

　　式中：X1为尺寸圆柱外径，mm；X2为侧板厚度，mm；X3为肋板厚度，mm；X4为减重孔长度，mm；X5为减重孔宽度，mm；X6为减重孔圆角，mm；X7为侧板宽度，mm。

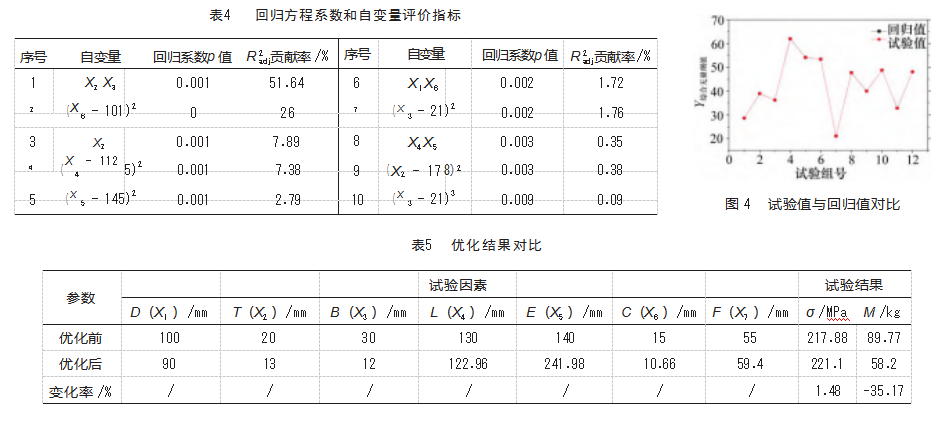
　　对式(3)回归方程进行拟合程度检验[18]。回归方程的统计量F=3 150 569.4，由于F的观测值落入拒绝区域：F=3 150 569.4>F1−α(dfR,dfE)=F0.95(6,10)=3.22，F统计量远大于F0.95(6,10)，所以回归方程是有显著意义的；从回归方程决定系数R2=100%和修正决定系数R=100%来看，其数值均为1，且决定系数R2和修正决定系数R两者相同，说明方程拟合很好，另外残差标准差S=0.006 986 04较小，说明观察值与拟合回归线的平均偏离程度很小，因此回归方程总效果很好；对回归方程各回归系数进行检验，结果如表4所示。线性自变量：X2 X3、X2、X1 X6、X4 X5，二次项自变量：(X6−101)2、(X4−112.5)2、(X5−145)2、(X3−21)2、(X2−17.8)2，三次项自变量：(X3−21)3系数的p值均小于0.05，说明以上自变量均显著。另外，由表4可知，X2 X3对Y综合无量纲影响最为显著，对回归方程修正决定系数Rdj贡献率为51.64%(表4中自变量列的R贡献率均包含有常数-6.16的贡献率)，即仅用参数X2 X3可解释试验数据X2、X3与Y综合无量纲之间信息量的51.64%。(X6-101)2的加入增加了26%的解释能力。同理X2、(X4-112.5)2、(X5−145)2、X1 X6、(X3−21)2、X4 X5、(X2−17.8)2、(X3−21)3分别为7.89%、7.38%、2.79%、1.72%、1.76%、0.35%、0.38%和0.09%。由于X2、(X2−17.8)2同为侧板厚度T(X2)，合并贡献率为8.72%。同理(X3−21)2、(X3−21)3合并，因此肋板厚度B(X3)贡献率为1.85%。最终可知，参数对Y综合无量纲影响的显著程度可排序为X2 X3＞X6＞X2＞X4＞X5＞X3＞X1 X6＞X4 X5。圆柱外径D(X1)侧板宽度F(X7)对回归方程不显著。

　　3.3回归方程的总结及拉板的结构参数优化

　　根据回归方程(3)以及表3中的试验方案可以做出试验值与回归值的对比图4。由图中可以看出，回归值与试验值结果吻合度较高，趋势基本一致。对回归方程规划求解，Y综合无量纲求最小值。将最优参数圆整后，参数为X1=90 mm，X2=13 mm，X3=12 mm，X4=122.96 mm，X5=241.98 mm，X6=10.66 mm，X7=59.4 mm，依据优化后的参数，带入拉板数模并进行有限元仿真，结果如表5所示。

　　4结束语

　　本文通过均匀设计方法，通过回归分析方法对拉板的结构参数进行了优化设计研究，结果如下。

　　(1)通过回归分析确定了影响拉板特性的主次要结构参数，显著程度由大到小依次排序为：侧板厚度T与肋板厚度B的交互作用、减重孔圆角C、侧板厚度T、减重孔长度L、减重孔宽度E、肋板厚度B、圆柱外径D与减重孔圆角C的交互作用、减重孔长度L(X4)与减重孔宽度E(X5)的交互作用。

　　(2)建立了拉板最大应力值、重量与结构参数的回归方程，检验了回归方程的显著性和总效果，以及回归系数的显著性，表明在设计空间内拉板的回归方程预测精度良好。

　　(3)依据拉板回归方程的规划寻优解，拉板优化后的模型比拉板优化前的模型最大应力值增大了1.48%，重量减少了35.17%。

　　参考文献：

　　[1]任永强,韩承芮.基于ANSYS Workbench的卡簧压装机机架拓扑优化设计[J].组合机床与自动化加工技术,2020(10):55-58.

　　[2]郑玉巧,和哲,张璐,等.基于均匀设计的风力机塔架结构参数优化研究[J].太阳能学报,2020,41(4):215-220.

　　[3]何鹏,梁裕如,段宏飞,等.基于均匀设计的制冷小管径涡流管结构优化[J].西安石油大学学报(自然科学版),2021,36(5):108-113.

　　[4]张荣锋,王勇,刘涛.基于灰色关联分析的芯片布局和散热器结构参数优化[J].装备环境工程,2021,18(6):136-144.

　　[5]Student P,Velcea D,Phd R,et al.STRESS FATIGUE LIFE OPTIMISATION OF AN AIRPLANE LANDING GEAR LEVER ARM USING ANSYS nCODE[Z].2015.

　　[6]吉梦雯.基于均匀设计的强力旋压连杆衬套工艺参数优化研究[D].太原:中北大学,2019.

　　[7]韩婕,李秋萍.基于均匀设计法的EⅡ型旋风分离器结构优化[J].天然气化工(C1化学与化工),2017,42(6):95-98.

　　[8]杨宇明,张新敏,王晓云.基于均匀设计的汽车变速杆操纵舒适性研究[J].机械工程师,2020(12):28-30.

　　[9]陈再现,钟炜彭,李秦鸣.基于均匀设计的模型更新混合模拟试验方法[J].振动与冲击,2020,39(21):9-16.

　　[10]Maochang Qiu,Jia Yao,Tuyi Zhong,et al.Thermal-mechanical Coupling Analysis of Rear Wheel Brake of Sightseeing Vehicle Based on Workbench[J].Journal of Physics:Conference Series,2021:012058.

　　[11]曾明玉,刘建永.H13钢激光仿生强化单元工艺研究[J].湖北汽车工业学院学报,2021,35(3):77-80.

　　[12]周万春,王启佳,孙维,等.基于ANSYS Workbench的刮板输送机中部槽优化设计[J].煤矿机械,2012,33(4):8-9.

　　[13]李志远,许娟红,魏涛,等.基于Workbench工装夹具设计与优化分析[J].机电工程技术,2017,46(11):14-16.

　　[14]方开泰,马长兴.正交与均匀试验设计[M].北京:科学出版社,2001.

　　[15]肖文,霍柱东,孙望.基于Ansys Workbench的高速连接器端子结构优化设计[J].机电工程技术,2020,49(7):244-245.

　　[16]邱东.谁是政府统计的最后东家[M].北京:中国统计出版社,2003.

　　[17]马逢时,刘传冰,周暐.六西格玛管理统计指南MINITAB使用指导[M].北京:中国人民大学出版社,2013.

　　[18]宋阳,李海亮.铅锌矿石小块体重多元线性回归方程的构建及其检验[J].甘肃冶金,2021,43(1):93-96.