摘要：针对传统故障诊断方法在小样本数据集下诊断准确率低且故障特征提取难的问题，提出了一种改进大津阈值分割算法(OTSU)和卷积神经网络(CNN)相结合的智能故障诊断方法。首先，对采集到的振动信号进行希尔伯特变换(Hillbert)得到信号的包络谱，同时使用小波变换对包络谱信号处理，获取二维特征时频图；其次，建立最大类间方差目标函数模型，通过算术优化算法(AOA)得到时频图的最佳分割阈值，再将变换后的阈值分割图像作为CNN的输入得到最优训练模型，最后得到分类结果。试验结果表明：所提方法相比于传统OTSU方法，所提取的故障特征更为突出，为模型提供了优秀的训练样本；在较小数据样本条件下，所提方法的准确率达99.01%，远高于传统故障诊断方法，且模型有着良好的泛化能力。

　　关键词：OTSU；故障特征提取；卷积神经网络；时频图

　　0引言

　　旋转机械运行的工况复杂、所处工作环境较为恶劣，而滚动轴承是旋转机械中的关键部件，具有传递扭矩，减少摩擦的作用，其健康状态直接影响旋转机械的性能。有超过30%的旋转机械发生故障是因为滚动轴承在长时间高负荷运行状态下发生故障引起的，继而产生一系列安全隐患。因此，研究一种准确可靠的轴承故障诊断方法具有重要的现实意义。

　　近几年来，随着深度学习的兴起，为故障诊断领域提供了新思路。学者们提出了将卷积神经网络(Convo⁃lutional Neural Network，CNN)运用到故障诊断中，CNN具有可以自动提取整合特征后通过分类器输出分类结果的特点，从而实现了轴承的智能故障诊断。曲健岭等[1]提出了一种基于一维神经网络的滚动轴承自适应故障诊断算法，其先对采集到的振动信号做重叠分段预处理，然后以时间序输入到一维卷积神经网络中提取特征，进而实现故障诊断；张立智等[2]利用卷积降噪自编码器对振动信号进行降噪、降维处理，然后将提取到的特征输入到CNN实现故障分类；吴东升等[3]先使用变分模态分解(VMD)对数据降噪处理，然后经过局部均值分解(LMD)得到PF分量，将经选择后的PF分量输入CNN中实现特征提取与分类；宫文峰等[4]提出一种基于改进卷积神经网络的滚动轴承故障诊断方法，该方法引入全局均值池化替代传统卷积神经网络的全连接层部分，从而实现了故障分类；刘颖等[5]提出一种先将振动信号进行小波包分解，再将分解求得的特征向量作为卷积神经网络的输入，实现了故障识别分类。

　　以上方法在轴承的故障诊断应用中可行，但由于受环境因素和载荷变化影响，采集到的振动信号在多级时间段特征频率异常，变化明显，受噪声干扰，信号具有高度复杂性、不确定性，多种信号高度耦合致使故障诊断精度低。采用一维信号输入CNN，在提取故障特征时由于噪声信号干扰会发生故障特征丢失的现象，而且网络计算易陷入局部最优，不利于快速且有效地得出最优训练模型。

　　因此，本文提出了一种基于改进OTSU方法的二维卷积神经网络(OTSU-CNN)的滚动轴承故障诊断方法。首先将采集到的振动信号做希尔伯特变换，然后将变换后的信号做Morlet小波变换得到时频图，通过算术优化算法(AOA)对OTSU阈值进行寻优得出最佳阈值，进而得到更好的故障特征提取效果图，将其传入CNN对模型进行训练，完成故障的分类，最后对故障诊断准确率进行测试。

　　1理论背景

　　1.1小波变换

　　小波变换(Wavelet Transform，WT)是提取时域、频域信息的重要方法之一[6-7]，其特点在于其可以对非平稳信号做时频分析。WT克服了短时傅里叶变换(Short-time Fourier Transform，STFT)窗口固定的缺点，为信号分析提供了随频率变化的时频窗。WT能够自适应时频信号分析需求，做到信号多尺度细化，即使高频处时间细分，低频处频率细分。WT变换公式如下：

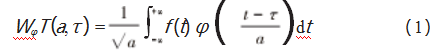
　　式中：a为尺度因子；τ为平移因子；φ为小波基函数。小波基的选择在轴承故障诊断中至关重要，本文选择Morlet小波[8]，该方法由法国科学家Morlet在研究地震波时提出的，Morlet复小波定义式ψ(t)如下：

　　式中：j为复数单位；σ为形状因子；t为采样时间；f0为中心频率。

　　Morlet小波的傅里叶变换频域形式如下：

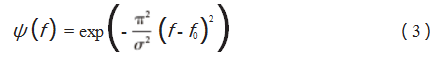
　　式中：ψ(f)为实函数。

　　1.2改进OTSU阈值分割算法

　　传统OTSU算法由学者Otus提出，是一种对图像进行二值化的自适应阈值确定算法[9]，因其以类间方差最大化为准则，故也被称为最大类间方差算法。

　　假设有灰度值为[0,L-1]，分辨率为N×M的图像T，将图像的灰度直方图归一化，得到像素概率pi为：

　　式中：ni为灰度级为i的像素个数。

　　假设任选分割阈值为α，将图像的像素分为C0与C 1，C0的灰度级区间为[0,1,…,α]，C 1的灰度级区间为[α+1,…,L-1]，二者概率计算如下：

　　通过AOA对阈值α进行寻优，找到最佳阈值。AOA是一种全局寻优的优化算法[10]，其先从随机生成的种群作为候选解X开始，通过不断迭代进行寻优。寻优过程为通过数学优化器加速函数(Math Optimizer Accelerat⁃ed，MOA)选择优化策略、乘法与除法策略全局搜索、加法与减法策略收敛解从而找出全局最优解。为得到最大类间方差来求得最佳阈值，将类间方差设置为目标函数。

　　AOA通过MOA选择搜索阶段，当r1＞MOA时执行全局搜索，r1＜MOA时执行局部开发阶段。

　　式中：t为当前迭代；T为最大迭代次数；RMin与RMax为优化器的最小值与最大值，取0.2与1.0；r1为0~1间随机数。

　　AOA执行全局搜索，位置不断更新，当r2＜0.5时，执行除法搜索策略；当r2＞0.5时，执行乘法策略，位置更新公式如下：

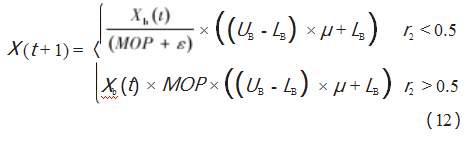
　　式中：r2∈[0,1]；Xb(t)为当前迭代下的最优解；μ为控制参数，取值为0.499，用于调整搜索过程；UB、LB为上、下界；ε为极小值。

　　其中，数学优化器概率(Math Optimizer Probability，MOP)计算公式如下：

　　式中：τ为敏感参数，取值为5，其作用是定义迭代过程中的局部开发精度。

　　AOA执行局部开发收敛解的位置更新公式如下：

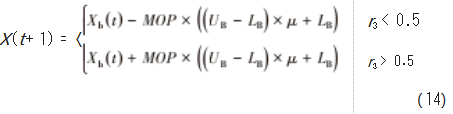
　　式中：r3为0~1间随机数。

　　1.3卷积神经网络

　　卷积神经网络(Convolutional Neural Networks，CNN)于20世纪60年代受生物科学启发提出来的一种前馈神经网络[11]，本质为多层感知机，其结构主要包括输入层、卷积层、池化层、全连接层。

　　其中，卷积层是神经网络的核心部件，通过卷积层来提取输入时频图的特征信息。

　　卷积运算公式如下：

　　式中：k为第i层第r个卷积核；b为对应的偏置；*为卷积运算；xi-1为第i-1层的输出数据。

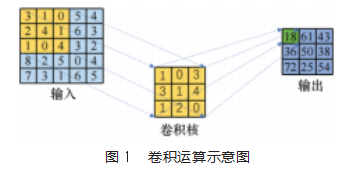
　　如图1所示，输入图中的输入子数组与卷积核中的数组按元素对应相乘并求和，得到输出中的对应元素。

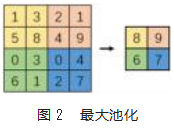
　　池化层是卷积神经网络另一关键部件，其本质为降采样，池化层将输入进来的图像划分为诸多子区域，子区域呈矩形，提取子区域中的最大值。池化层的加入，使得数据空间减小，参数计算量下降，在一定程度上防止了过拟合，扩大了感受野，并且池化层具有特征不变性。最大池化作用过程如图2所示。

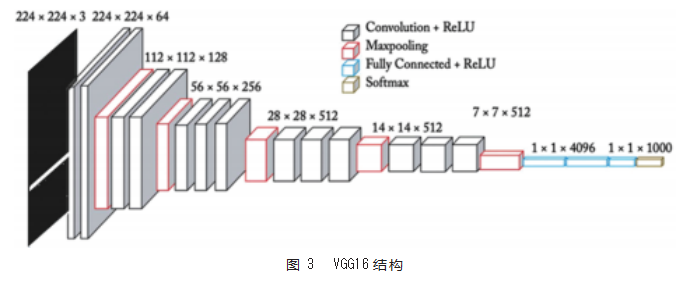
　　本文选用VGG16卷积神经网络模型，VGG16在分类任务中表现良好，且VGG16主体结构是由多个小卷积核组成，有13个卷积层与3个全连接层，采用2×2的最大池化，VGG16模型如图3所示。为防止VGG16发生梯度爆炸，故在原模型中加入BN(Batch Normalization)层，其原理为在后续每一层输入前插入一个归一化层，再将数据送入下一层。在BN层后添加激活层，激活层使用收敛更快的ReLU激活函数，ReLU函数有着更为宽阔的兴奋边界，能够单侧抑制。最后，在模型每两层末添加Dropout层，防止模型过拟合。

　　2基于改进OTSU和CNN的故障诊断

　　AOA阈值调优过程如图4所示。改进OTSU与CNN相结合的滚动轴承故障诊断流程如图5所示。

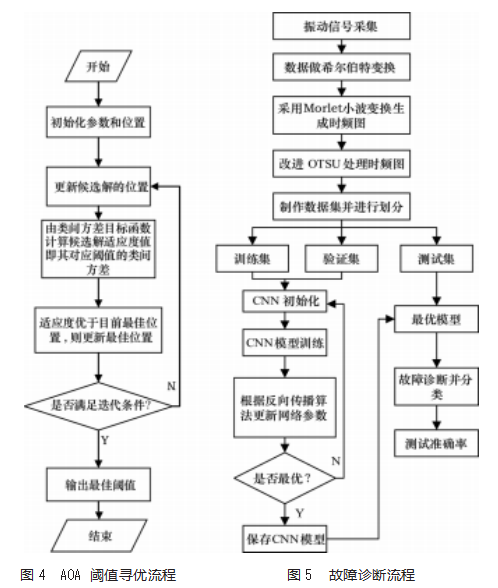
　　具体实现步骤如下：

　　(1)通过Hillbert变换处理采集到的振动信号，Hill⁃bert处理后得到包络谱信号；

　　(2)将经Hillbert变换后得到的信号做Morlet小波变换得到时频图；

　　(3)时频图经改进OTSU处理，处理后的图像制作数据集并进行打乱编码划分；

　　(4)将数据集打乱按比例分为训练集、验证集与测试集，并将训练集送入CNN模型中训练网络模型，通过优化算法对模型不断进行参数调优；

　　(5)保存好最优的训练模型并利用最优模型测试测试集数据，得到分类结果继而进行分析。

　　3实验验证与分析

　　3.1实验数据集

　　本文选用经典数据集凯斯西储大学(CWRU)轴承数据集，实验平台包含一个2马力(1.5 kW)的电动机以及一个扭矩传感器/译码器、一个功率测试计和电子控制器。采用电火花加工人为制造故障，使用加速度传感器来采集振动加速度信号，扭矩传感器用来搜集速度以及功率数据。实验平台如图6所示[12]。本文选用驱动端轴承，型号为SKF6205，振动信号由采样频率为12 kHz的数据记录仪采集得到。选取0.177 8 mm以及0.533 4 mm损伤直径下的正常、内外圈以及滚动体故障数据，取样长度为1 024，分为10种类型如表1所示。数据集样本数量为10 000，每种类型1 000个样本，按6∶3∶1乱序将数据集分为训练集、验证集以及测试集，训练集和验证集用于对网络模型进行训练。

　　3.2数据预处理

　　本文的实验硬件环境为intel i5-12500H、NVIDIA RTX3050Ti以及16G内存，软件环境为MATLABR2020a，基于Tensorflow开发框架。

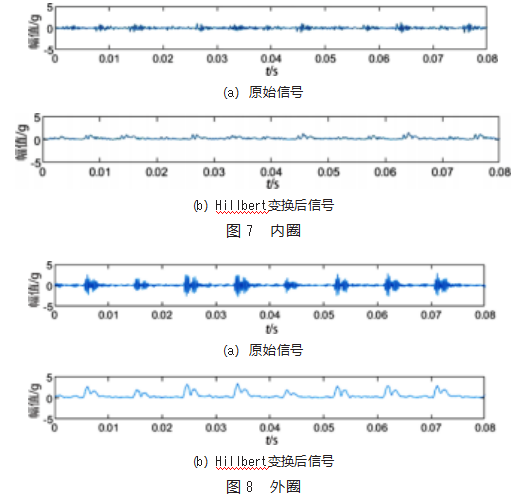
　　滚动轴承振动原始信号较为杂乱，需先经Hillbert变换后得到包络谱信号，如图7、图8所示，依次为内圈、外圈及其Hillbert变换，经变换后可以去除无用信号，保留特征信号。

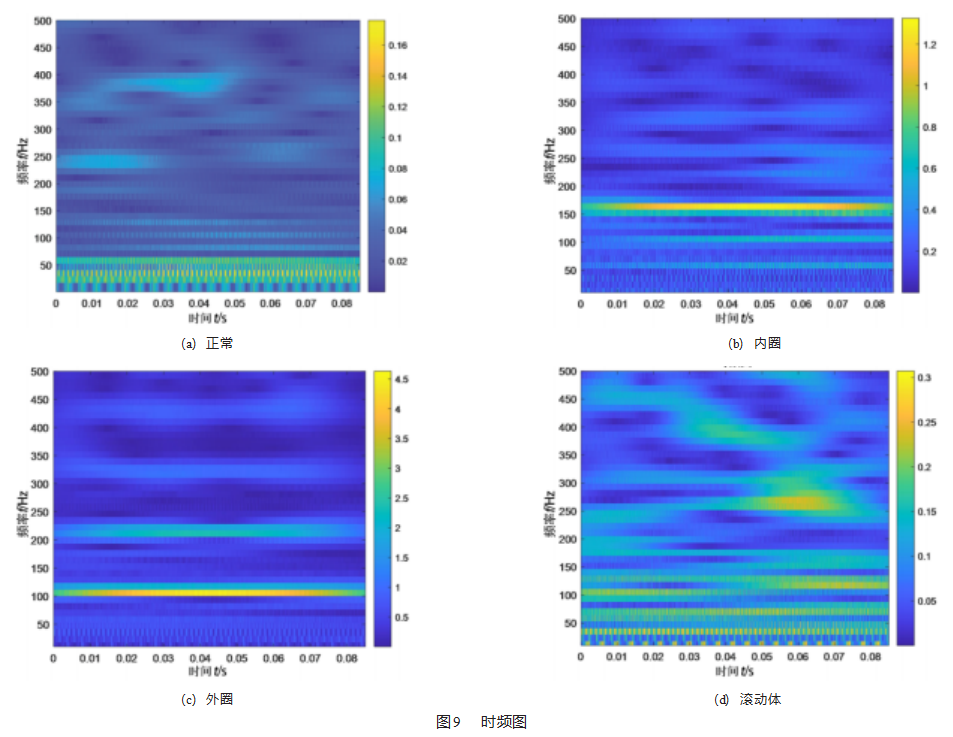
　　对振动信号经Hillbert变换后得到的包络谱信号做Morlet小波变换，得到时频图，时频图如图9所示，限于篇幅仅展示故障直径为0.177 8 mm，转速1 797 r/min时频图。

　　输出的图像像素为434×343，将输出图像做OTSU变换与改进OTSU变换，分别计算出最优阈值后将图像二值化。这里以内圈为例，传统OTSU内圈的最优阈值为α=0.588 2，改进OTSU通过寻优得到内圈的最优阈值为α=0.6637。图像中像素的灰度值小于该阈值，其像素对应的灰度值设置为0，否则设置为255，变换后图像如图10所示。从图中可以看出，未改进的OTSU提取162.18 Hz的内圈故障频带夹杂噪声信号较为明显，而改进后的OTSU提取到的故障频带达到很好的提取效果。

　　3.3实验与分析

　　将训练集送入网络模型中进行训练，网络具体参数配置为BatchSize=16，Kernelsize=3，epoch=30。选用Ad⁃am优化器，学习率为0.001。全连接层后输出分类结果设置为10类，损失函数选用交叉熵损失函数，Dropout层设置为0.5，即每次迭代有一半的神经元随机舍弃，减少特征冗余。

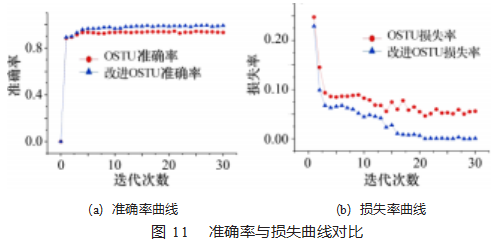
　　网络模型经30次迭代训练后得到如图11所示结果，由图可得网络模型在传统OTSU方法上准确率为94.30%，在改进OTSU方法上准确率为99.01%，而且收敛速度快，在15次迭代后趋于稳定，模型有着良好的鲁棒性。

　　实验中引入混淆矩阵来可视化分类结果，混淆矩阵中每一行为真实标签，每一列为预测标签，混淆矩阵反映了分类模型整体的预测结果，通过混淆矩阵可以观测到误判类型与误判样本数量。混淆矩阵中主对角线为正确预测的样本数量。混淆矩阵如图12所示。

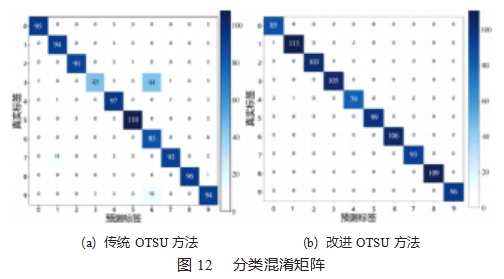
　　通过混淆矩阵可以看出，改进前有44个故障直径为0.177 8 mm、转速为1 797 r/min的滚动体故障样本被错误识别为相同故障直径下，转速为1 772 r/min的滚动体故障，而本文方法在相同工况下，全部识别正确。且本文方法在测试集上整体表现准确率为98.60%，说明本文方法能够有效地对滚动轴承故障进行诊断。

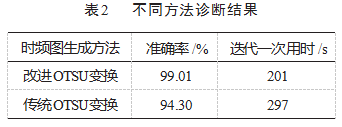
　　为验证本文方法的优越性，将本文基于传统OTSU变换方法与改进OTSU变换方法输入时频图做对比，对比结果如表2所示。经改进OTSU变换的方法准确率达99.01%，CPU运行条件下迭代一次用时201 s；经传统OTSU变换的方法准确率为94.30%，CPU运行条件下迭代一次用时297 s。经改进OTSU变换较传统OTSU方法诊断迭代一次时间缩短32.3%且准确率提高了4.71%，说明经改进OTSU方法处理，故障特征更为明显，其他非敏感信息比例降低，网络识别效率更高。

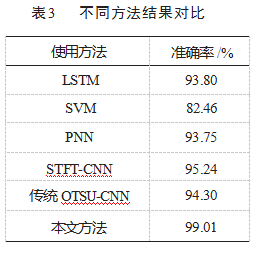
　　将本文方法与其他文献中方法做对比，比较结果如表3所示。通过对比，可以得出本文方法在多分类轴承故障诊断任务中相较于SVM[13]、LSTM[14]、PNN[15]等故障诊断方法，本文方法有更高的准确率；相较于同为时频图输入的STFT-CNN[16]，本文方法要优于STFT-CNN方法。验证了该方法在故障诊断中的优越性。

　　4结束语

　　本文提出了一种基于改进OTSU方法的二维卷积神经网络轴承故障诊断方法，首先将采集到的振动信号做Hillbert变换，然后将变换后的信号做Morlet小波变换得到时频图，时频图再经改进OTSU方法生成故障特征清晰的时频图，最后将经改进OTSU方法得到的时频图送往卷积神经网络，对模型进行训练。得出结论：本文采用的方法整体能达到99.01%的准确率，相较于传统特征提取方法，本文方法有着更高的准确率，相较STFT与传统OTSU方法，本文在转换二维图像时能够有效的提取故障特征且故障特征更为明显，经改进OTSU方法后显著降低了其他非敏感信息的比例，为神经网络训练提供了优秀的样本。该方法为基于深度学习的轴承故障诊断提供了新思路且具有较好的应用价值。

　　参考文献：

　　[1]曲建岭,余路,袁涛,等.基于一维卷积神经网络的滚动轴承自适应故障诊断算法[J].仪器仪表学报,2018,39(7):134-143.

　　[2]张立智,井陆阳,徐卫晓,等.基于卷积降噪自编码器和CNN的滚动轴承故障诊断[J].组合机床与自动化加工技术,2019(6):58-62.

　　[3]吴东升,杨青,张继云,等.基于VMD-LMD-CNN的集合型故障诊断方法[J].轴承,2020(10):57-63.

　　[4]宫文峰,陈辉,张泽辉,等.基于改进卷积神经网络的滚动轴承智能故障诊断研究[J].振动工程学报,2020,33(2):400-413.

　　[5]刘颖,陶建峰,黄武涛,等.小波包能量与CNN相结合的滚动轴承故障诊断方法[J].机械设计与制造,2021(11):127-131.

　　[6]袁建虎,韩涛,唐建,等.基于小波时频图和CNN的滚动轴承智能故障诊断方法[J].机械设计与研究,2017,33(2):93-97.

　　[7]程军圣,于德介,邓乾旺,等.连续小波变换在滚动轴承故障诊断中的应用[J].中国机械工程,2003(23):64-67.

　　[8]艾延廷,田博文,田晶,等.Morlet复小波频带优化及其在中介轴承故障诊断中的应用[J].航空动力学报,2020,35(1):153-161.

　　[9]严晨曦,熊凌.基于改进的Otsu方法的钢渣彩色图像分割[J].计算机工程与设计,2020,41(9):2585-2591.

　　[10]Abualigah L,Diabat A,Mirjalili S,et al.The Arithmetic Optimiza⁃tion Algorithm[J].Computer Methods in Applied Mechanics and Engineering,2021(4):113609.1-113609.38.

　　[11]GOODFELLOW I,BENGIO Y,COURVILLE A.Deeplearning[M].The MIT Press,2016.

　　[12]宫文峰,陈辉,张美玲,等.基于深度学习的电机轴承微小故障智能诊断方法[J].仪器仪表学报,2020,41(1):195-205.

　　[13]INCE T,KIRANYAZ S,EREN L,et al.Real-time motor fault de⁃tection by 1-D convolutional neural networks[J].IEEE Transac⁃tions on Industrial Electronics,2016,63(11):7067-7075.

　　[14]PAN H,HE X,TANG S,et al.An improved bearing fault diagno⁃sis method using one-dimensional CNN and LSTM[J].Journal of Mechanical Engineering,2018,64(7/8):443-452.

　　[15]刘乐,孙虎儿,谢志谦.基于SVD-LMD模糊熵与PNN的滚动轴承故障诊断[J].机械传动,2017,41(3):172-176.

　　[16]李恒,张氢,秦仙蓉,等.基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J].振动与冲击,2018,37(19):124-131.