摘要：轮式牵引器驱动轮常被设计为近似齿轮的外形，但不合理的接触正压力加快驱动轮齿形压溃和磨损，降低驱动轮和套管的摩擦性能和越障能力，因此需要通过控制液压系统输出性能合理匹配驱动轮接触正压力。针对此问题建立了100~150 mm套管中液压缸活塞杆位置和驱动轮正压力之间的力学关系，利用AMEsim软件建立120 mm套管推靠机构的二维机械结构和液压系统仿真模型，联合Simulink建立液压缸输出位置的模糊PID控制，研究液压系统输出特性及驱动轮接触正压力和驱动臂、推靠臂的运动学性能。仿真结果表明：在120 mm套管中通过模糊PID控制的液压缸活塞杆输出位置，整个过程中液压缸活塞杆输出位置稳定时最大误差0.5 mm，接触正压力最大误差为5.24 N，驱动轮和套管壁接触稳定，推靠臂、驱动臂转速合理且不会产生过大冲击，验证了方法的可行性和可靠性，为后续轮式牵引器优化提供依据。

　　关键词：轮式牵引器；AMEsim/Simulink联合仿真；液压缸；模糊PID控制

　　引言

　　水平井技术诞生于20世纪后期并成功应用于油气工业中，成为油气开采的主要施工方案。到2012年，我国已经成功钻探了2 300多口水平井[1]。水平井钻井、测井过程中所需的仪器设备无法依靠重力下放到工作位置，需要依靠具有动力源的工具将钻井、测井等仪器设备送到设定位置[2]。因此先后出现轮式牵引器、伸缩式牵引器、履带式牵引器[3]，根据动力源又可分为液压驱动、电机驱动。液压轮式牵引器兼具液压式和轮式的优点，具有可靠性好、效率高、能够适应复杂的井下工况等显著特点而被广泛应用。轮式牵引器为了增大牵引力、提高牵引器的越障能力，设计为带有齿的驱动轮。齿形状驱动轮的齿形磨损和压溃导致牵引性能下降[4-5]，因此需要对牵引器的牵引器力与外界负载相匹配合理的接触正压力值，驱动轮接触正压力源于液压系统液压缸的输出特性。范强等[6]利用AMEsim对轮式牵引器的液压系统进行了定量分析，研究了不同流量下摆臂的运动速度，但摆臂的稳定时有较大速度波动大和冲击。洪诗益等[7]利用AMEsim和Simulink联合仿真对轮式牵引器推靠装置的液压系统进行研究，得到模糊PID控制液压缸的输出具有更好的控制效果。但均未建立完整的机电液联合仿真模型，对液压系统输出和驱动轮接触正压力之间的关系及结构运动学进行研究。

　　针对此问题，本文根据液压轮式牵引器的工作原理，建立液压缸活塞杆位置和正压力之间的数学关系，建立推靠装置机电液联合仿真模型，通过液压系统的控制，研究分析牵引器的推靠机构工作特性，验证了液压系统控制推靠机构的合理性。

　　1轮式牵引器驱动机构原理

　　轮式牵引器驱动机构如图1所示，主要由驱动臂、推靠臂、链轮传动、驱动轮、复位弹簧、压力弹簧、锥齿轮组等部件组成。

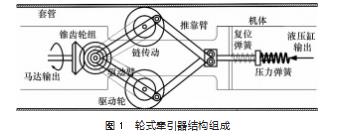
　　牵引器以液压系统为驱动，液压缸活塞杆移动压缩压力弹簧推动推杆轴向移动压缩复位弹簧，推杆推动推靠臂传递动力给驱动臂，使得驱动臂绕固定点转动直至驱动臂上驱动轮和套管接触产生接触力，通过控制液压缸活塞压缩位置对压力弹簧的压缩量控制接触力大小。驱动轮接触套管壁产生接触力后液压马达工作，带动锥齿轮组将驱动扭矩转换到两个驱动臂，驱动臂用链轮传动传递扭矩到驱动轮，控制液压马达输出转向实现牵引器前进和后退。结束工作时，液压马达停止工作，液压缸活塞杆收回，在复位弹簧的作用下收回驱动轮到初始位置。

　　驱动机构液压系统主要包含液压缸、液压马达的控制，两者为不同的回路且相互协同、独立工作。本文对推靠机构液压系统进行研究，研究液压缸活塞杆位置控制下的推靠机构特性和液压系统输出特性。

　　2推靠机构液压系统力学建模

　　2.1力学建模

　　构建液压系统的核心在于研究液压系统的理论输出特性，首要建立轮式牵引器驱动机构的力学模型。根据图1的推靠机构原理，对模型进行简化以降低模型复杂程度，本文主要对驱动臂、推靠臂、复位弹簧、压力弹簧进行研究，建立力学分析如图2所示。以驱动臂固定铰链点为坐标原点O建立xOy坐标系，根据力学分析可以运用虚功原理进行计算。虚功原理：即对于具有理想约束的质点系，平衡的充分条件是作用于质点系的主动力在任何方向上的和等于零。

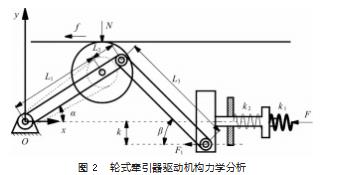
　   上述式(1)~(5)和图2中，L1为驱动轮中心到O点的距离；L2为驱动轮中心到支撑臂和推靠臂铰点的距离，L3为推靠臂的长度，α为驱动臂与x轴的夹角，β为推靠臂与x轴的夹角，h为推靠臂上弹簧偏离轴心的位置，k1为压力弹簧的弹性系数，k2为复位弹簧的弹性系数，N为驱动轮和套管间的正压力，F1为推靠臂的推力，f为单节驱动机构的牵引力，F为液压缸活塞杆推力。

　　2.2液压缸参数匹配

　　根据驱动机构的工作原理可知，牵引器推靠机构的行程确定包含两部分：爬行器工作的管径和爬行器施加的推靠力。工作管道确定的行程也就是复位弹簧的压缩距离Δx2，即驱动轮在原始位置到接触套管壁时的行程；爬行器施加推靠力的行程为Δx 1，即产生最大接触力时压力弹簧的压缩量，因此液压缸活塞的理论行程为：

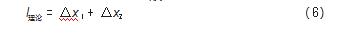
　　表1所示为牵引器驱动机构参数[8]。本文设置推靠臂初始位置的夹角α′=15°。在理论分析的基础上，利用Matlab数值分析对数学模型进行求解，确定驱动轮和管道壁接触时液压缸的位移关系如表2所示。

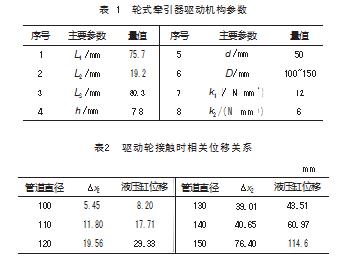
　　液压缸活塞杆位置和接触正压力之间的关系如图3所示。由图可知，随着管道直径从100 mm增大到150 mm的过程中，爬行轮接触管道壁开始产生正压力的液压缸活塞杆位移增加。100~150 mm管径接触套管壁后的直线斜率分别为：6.834、8.407、10.521、12.527、15.587、20.413，说明在套管直径增大的情况下，压力弹簧的作用力得到更好地放大。

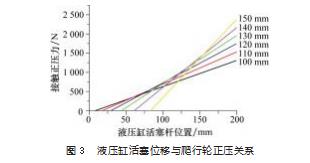
　　国内两组驱动四轮牵引器最大牵引力大于4 000 N，因此单轮产生的牵引力大于1 000 N，驱动轮和管道间的摩擦因数μ=1.046[7]，因此单轮和管道间产生的正压力应大于956 N。

　　根据图3可知，在管道直径为100 mm时，产生956 N的正压力需要液压缸活塞杆的压力为1 712.8 N，取安全值2 000 N，则液压缸有效工作面积为：

　　活塞杆受压，液压活塞杆受压，取d′=0.6。得到D=22.6 mm。根据液压缸内径系列选取规则取D=32 mm，液压缸活塞杆直径为10 mm，长度210 mm。

　　3 AMEsim-Simulik的推靠机构机电液联合仿真

　　为了分析液压系统的输出动态特性、提高系统的稳定、研究牵引器的推靠机构特性，本文对轮式牵引器进行机电液联合仿真分析。在AMEsim软件中设置Simulink联合仿真环境，Simulink中建立模糊PID控制模型，通过S-function函数调用AMEsim中的仿真模型进行联合仿真。

　　3.1 AMEsim机电夜仿真模型建立

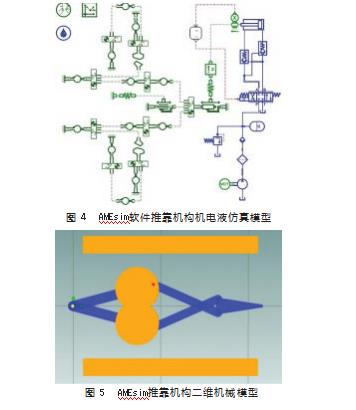
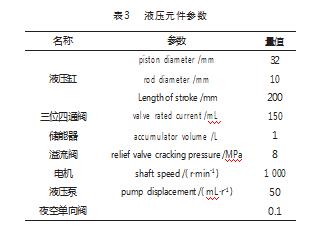
　　在AMEsim软件中，根据图1牵引器推靠机构的原理和表1中的参数，运用2D Mechanical库搭建套管、驱动臂、推靠臂、推杆，利用移动副、旋转副连接各构件，设置驱动和套管间的接触模型，在1D Mechanical中构建压力弹簧、复位弹簧；机电液联合仿真模型如图4所示[9-11]，二维机械模型如图5所示，为初始位置。液压元件参数如表3所示。

　　3.2液压系统模糊PID控制

　　(1)控制原理

　　如图6所示，液压缸活塞杆位置控制过程中，首先通过位移传感器检测液压缸活塞杆的实际位置，实际位置和给定期望位置比较得到偏差信号，将偏差信号输入到模糊控制器中，模糊控制器对PID控制参数进行优化，得到三位四通电磁阀的控制量，进而调节液压缸活塞杆的输出位置[12-13]。

　　(2)液压缸活塞杆位置模糊PID控制

　　模糊控制是以模糊理论、模糊语言变量和模糊逻辑推理的一种智能控制方法，核心部分为模糊控制器，控制规律由计算机的程序实现。模糊控制器输入变量为e(误差)和ec(误差变化)，e的论域为[-1 1]，ec的论域为[-1 1]。控制量ΔKp、ΔKi、ΔKd的论域为[-10 10]、[-5 5]、[-5 5]。当液压缸活塞杆位置发生变化时，模糊控制器可以实时监测系统偏差e与偏差的变化率ec并持续修正Kp、Ki、Kd三个参数，因此模糊PID控制具有良好的控制性能[14-16]。图7为Simulink模糊PID控制模型。

　　4仿真结果分析

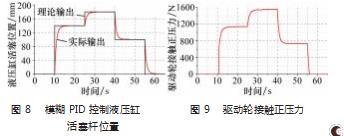
　　本文以直径为120 mm的套管为例，验证液压缸活塞杆位置，通过控制液压缸活塞杆的位置控驱动轮的接触性能，液压缸活塞杆理论输出位置如图8理论输出所示。仿真结果如下。

　　(1)液压缸活塞杆位置验证

　　液压缸活塞杆位置如图8所示。由图可知，通过对比理论输出和实际输出，模糊PID控制可以合理地控制液压缸活塞杆的输出位置，控制的核心在于尽可能地控制液压缸活塞输出的精度和稳定性，适当地调节系统的响应时间，避免驱动轮和套管产生过大的冲击碰撞。通过图8可知模糊PID控制下系统的响应时间大约为7 s左右，稳定后控制精度误差为0.5 mm，符合控制要求。

　　(2)驱动轮接触正压力验证

　　驱动轮接触套管的接触正压力如图9所示。通过图9并参考图8可以看出，液缸10 s开始工作，经过0.75 s驱动轮和管道壁产生接触力，在17.5 s活塞杆处于140 mm位置对应的正压力为1 133.77 N，在32.7 s活塞杆处于180 mm对应的接触正压力为1 548.34 N，在48.2 s活塞杆处于100 mm对应正压力为729.62 N，55 s开始活塞杆收回经过1.04 s接触正压力为0 N。根据式(9)计算140 mm、180 mm、100 mm的理论接触正压力分别为：1 134.41 N、1 544.43 N、724.38 N，误差分别为：0.64 N、3.91 N、5.24 N，验证了通过控制液压缸活塞杆位置控制接触压力的合理性。

　　(3)驱动臂、推靠臂运动特性

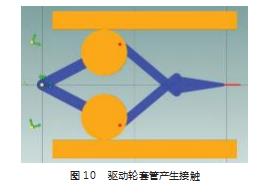
　　驱动机构驱动轮仿真过程中接触套管壁如图10所示，驱动臂相对转角、转速如图11所示。从图11中可以看出是上方位驱动臂，在10 s液压缸开始工作后相对转角逆时针转动12.544°并持续保持稳定，直至55 s后液压缸活塞杆收回到0 mm时，由于复位弹簧的作用，驱动臂收回过程中，随着复位弹簧弹力减小，收回速度降低。在此过程中驱动臂的最大转速为-4.56 r/min。

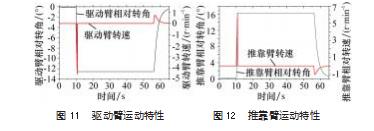
　　推靠臂相对转速、转速如图12所示。从图中可以看出是上方位推靠臂，在10 s液压缸开始工作后推靠臂相对转角顺时针转动16.3°保持稳定值，直至55 s后液压缸活塞杆收回到0 mm时，驱动臂的最大转速为6.13 r/min，也不会出现过大的冲击。

　　5结束语

　　本文针对水平井牵引器推靠机构，建立了驱动轮接触正压力和液压缸活塞位置的数学模型，利用AMEsim和Simulink建立牵引器推靠机构机电液联合仿真模型，设计了模糊PID控制，对120 mm套管的工况进行仿真分析，对比理论和仿真验证了数学模型、控制模型和液压系统的合理性并得到如下结论。

　　(1)根据驱动机构的原理，建立100~150 mm管道下驱动轮接触正压力和液压缸活塞杆位置之间的关系，在100 mm时要达到牵引力不小于4 000 N时液压缸的最小输入压力为1 712.8 N，且驱动轮接触正压力随着套管直径的增大而增大，即在较大的套管中会产生更大的牵引力。

　　(2)通过AMEsim/Simulink建立了推靠机构机电液联合仿真模型，通过模糊PID可以准确稳定地控制液压缸活塞杆位置，得到活塞杆输出稳定时位置误差为0.5 mm左右，响应时间大约为7 s。驱动轮接触正压力稳定时最大误差为5.24 N，验证了通过控制活塞杆位置控制接触压力的可行性。

　　(3)通过对驱动臂、推靠臂的相对转角和转速分析，在液压系统的驱动下驱动臂和推靠臂平稳可靠，转速较小，因此不会产生冲击碰撞，验证了控制的可行性。

　　参考文献：

　　[1]Liu Q,Zhao J,Zhu H,et al.Review,classification and structural analysis of downhole robots:Core technology and prospects for ap⁃plication[J].Robotics&Autonomous Systems,2019.

　　[2]高峰,吴庆,詹保平,等.蠕动式石油井下爬行器液压系统的设计与研究[J].机电工程,2019,36(3):257-261.

　　[3]刘清友,董润,耿凯,等.井下机器人研究进展与应用展望[J].石油钻探技术,2019,47(3):50-55.

　　[4]王锡磊,刘先平,李卫强,等.旋转轮式爬行器问题分析与解决[J].石油和化工设备,2020,23(12):59-61.

　　[5]潘明宇,姚劲松,潘为之.TRHW爬行器井下仪故障分析与解决[J].石油管材与仪器,2020(6):95-97.

　　[6]范强.轮式液压牵引器的结构设计与仿真分析[D].西安:西安理工大学,2016.

　　[7]洪诗益,吴伟,刘斌.基于AMESim与Simulink的液压牵引器驱动机构联合仿真[J].机电工程技术,2021,50(1):67-70.

　　[8]吴伟,李博,刘娜娜,等.轮式牵引机器人优化设计及运动特性分析[J].系统仿真学报,2020,32(5):918-926.

　　[9]肖晓华,代继樑,王昆鹏,等.基于黏着理论的牵引器驱动轮力学分析及优化[J].石油机械,2021,49(3):25-33.

　　[10]管建峰,王远飞,徐权鑫.基于AMESim的8t液压港口机械升降回路设计与优化[J].常熟理工学院学报,2021,35(5):43-45.

　　[11]张旭飞,邵焱,付玉琴,等.起重机变幅系统Simcenter 3D机液联合仿真分析[J].机械工程学报:1-8[2022-12-19].http://kns.cnki.net/kcms/detail/11.2187.TH.20220527.1452.083.html

　　[12]寇明坤.基于模糊自适应PID的定量泵-变量马达速度控制系统研究[D].西安:长安大学,2020.

　　[13]蒲虹云,蒋刚,郝兴安,等.基于变模糊PID控制器的阀控非对称缸复合控制策略[J].液压与气动,2022,46(11):82-89.

　　[14]杨韩峰,郭彦青,张宏,等.基于电磁换向阀的液压缸位置控制系统研究[J].机械设计与制造工程,2020,49(2):101-104.

　　[15]穆洪云,罗艳蕾,杜威,等.基于BP-PID的双液压缸电液同步控制仿真研究[J].液压气动与密封,2022,42(9):14-18.

　　[16]曹羽昕,沙鸿飞.基于模糊-遗传算法的PID除氧器液位控制系统[J].化工自动化及仪表,2022,49(5):580-584.