摘要：外界未知扰动对于高速旋转的磁悬浮转子的稳定性有着重要影响，因此磁悬浮轴承抗扰性能的高低决定了在高转速运行状态下转子能否安全稳定地运行。为此设计了一种基于等价输入干扰与滑模观测器的主动控制系统，用于磁悬浮轴承的转子位置控制。首先分析了磁悬浮轴承系统的结构及其工作原理，建立磁悬浮轴承系统线性化控制模型，并将原控制系统等价为一个等价输入干扰控制系统(EID系统)；然后设计滑模观测器以观测外部扰动；最后，基于等价输入干扰方法将干扰前馈到输入端，实现了外部扰动的有效抑制。通过对比仿真结果证明，在不牺牲控制性能的前提下，所设计的基于等价输入干扰滑模观测器较之于传统的龙伯格观测器有更好的抗扰动效果。

　　关键词：磁悬浮轴承；PID；等价输入干扰估计器；滑模观测器

　　引言

　　磁悬浮轴承(Active Magnetic Bearing，AMB)是种通过磁场使例如转子的旋转组件与轴承静置部位保持相对稳定距离的装置，距离内无机械接触，使得转子在旋转时与静置部位无机械摩擦[1]，这种新型的非接触式轴承能利用电磁力改变传统轴承机械摩擦大的缺点，得以使轴承发展步入到更高速度、更少磨损的新台阶。

　　目前磁悬浮轴承在各个领域都有应用。例如磁悬浮飞轮储能[2]、电力系统[3-5]、磁悬浮多电航空发动机[6-7]领域中。在这些应用领域中，磁悬浮轴承绝大多数运行在超高转速的状态下，若转子受扰动作用偏离预定位置过多，转子与定子发生机械摩擦，会造成严重机械损坏甚至导致系统崩溃，为解决上述问题，需要设计一个控制器控制转子平衡，并能实时对外部未知扰动进行观测，从而削弱扰动给系统带来的影响。很多传统方法均是被动控制[6-7]。数字控制则有模糊控制[8]、滑模控制[9]、神经网络[10]等对磁悬浮转子控制。如Tang Liang等[11]对平衡量未知的转子，通过动、静不平衡量的辨识与补偿控制设计了自适应对中控制器来消除颤动。Se Young Yoon和SL Chen等[12-14]将不平衡补偿技术扩展到控制回路中达到振动控制。

　　以上方法对于自身颤动有较好的抑制能力，但对于外部扰动的及时补偿能力稍有不足，因此对于外界不确定干扰，需要设计观测器对系统内部及未知干扰进行实时观测，并能够对磁轴承系统及时进行抗干扰控制。相对于传统的龙伯格观测器。滑模观测器(Sliding-Mode Observer，SMO)不仅将系统观测器观测误差线性方式反馈,而且还能够根据观测误差进行快速调整，从而实现对系统状态变量以及外部扰动及时快速并准确地估计[15]。

　　等价输入干扰通过观测器推测出一个等价输入干扰，前馈到控制器输入端，对扰动进行及时补偿，不需要掌握外部未知干扰的信息，目前该方法在各方面都有成功运用，如DC-DC变换器[16]、建筑抗震[17]、液压系统[18]、永磁同步电机[19]等。本文在滑模观测器上引入等价输入干扰补偿的设计思想设计伺服控制器[20-21]，以消除扰动对系统产生的影响[22]，实现对给定转子位置的高精度控制并使系统拥有高抗扰性能。

　　1数学模型

　　磁悬浮轴承利用电磁力使转子处于无接触悬浮状态，定子与悬浮转子之间没有机械接触，无摩擦。其通过位置传感器监测转子的位置偏移量，将其转换成电信号反馈到控制器，控制器控制电磁铁使转子的重心固定在运转的预定轨道上，使整个系统工作在安全状态，其原理如图1所示。

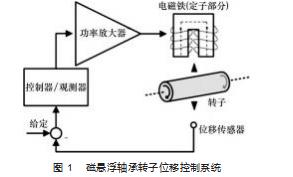
　　其控制对象单自由度AMB中电磁铁部分的线圈环绕匝数为N，S为有效磁极，初始时刻电磁线圈电流为i0，并作如下假设。

　　(1)由于对转子的控制在竖直方向，为方便计算忽略磁悬浮轴承转子的体积，可以将悬浮的转子简化一个质点。

　　(2)不考虑绕组漏磁通、磁滞等对系统的影响，且忽略定子与转子之间产生的磁阻。

　　电磁力的推导式如下：

　　此外，给定位置参考信号表示为yc(t)，将位置跟踪误差定义为e(t)=y(t)−yc(t)。对于系统所设计的观测器以及控制器，使观测误差在系统内部不确性变化和外部未知干扰影响的情况下需要快速稳定收敛到零，即当t→∞时，有e(t)→0。因为Ki/m≠0，易知该系统是可控可观测的。

　　2 EID滑模观测器控制系统设计

　　针对悬浮转子的稳定性抗干扰控制提出了一种基于等价输入干扰估计器与滑模观测器结合的PID控制方法，其内部控制系统结构如图2所示，由滑模观测器将系统内部参数的不确定参数变化和外部干扰转化为电信号，施加在控制器输出端，然后采用等价输入干扰滑模观测器对系统状态变量及外部干扰的进行等价输入干扰估计，并将估计值信号前馈到输入端后得到最终叠加后的控制方法。

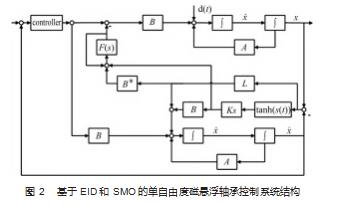
　　2.1等价输入干扰滑模观测器的设计

　　其状态方程如式(5)所示。对于此，再设计滑模观测器对EID系统其状态变量及干扰予以观测并等价估计。选择系统实际输出量和观测器输出量之间的观测误差的双曲正切函数作为滑模观测器的控制律。相比于符号函数更有效抑制滑模观测器在滑模面附近产生的抖动，同时还能够输出稳定准确的观测器输入。对于以上引入EID的新系统设计滑模观测器：

　　选取李雅普诺夫函数为V=ePex作为所设计部分稳定性的判断方法，其中P矩阵正定并且对称。然后对V(t)求导可得：

　　证明了所提出的观测方法能够保证系统全局一致并且最终有界的。

　　2.2闭环系统稳定性分析

　　一个控制系统中如果A满足Hurwitz稳定，那么其闭环系统将是是全局一致并且最终有界。那么有A11与A22是Hurwitz稳定的。

　　将控制律u(t)=(t)-d~e(t)代入原系统对应的EID控制系统中：

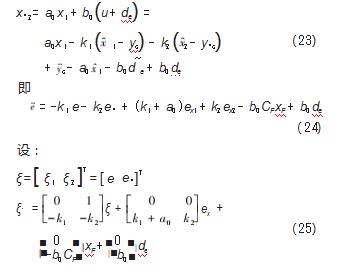
　　因为tanh(Ce)∈(-1，1)，假设de有界，则Λ有界。适当选取观测器增益L和低通滤波器F(s)，可确保A11和A22是Hurwitz稳定的。因此对于包含未知扰动量系统是最终全局一致有界的。

　　3仿真和实验验证

　　3.1主动磁悬浮轴承参数

　　采用MATLAB/Simulink对单自由度主动磁悬浮轴承系统和所提控制方法进行数值仿真和验证，其中本次设计的控制器控制对象单自由度磁悬浮轴承系统各参数如表1所示。

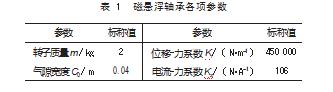
　　最后，仿真结果将采用时间乘绝对误差积分准则(ITAE)和均方根误差(RMSE)两项指标来定量分析[24]，仿真和实验采样周期均为0.01 s。

　　PID+EIDSMO方法参数如下：

　　观测器增益L=[45 000 000 100 000]T，滑模增益=50 000，取扰动的最高频率ωr=0.5π。

　　3.2观测器设计仿真结果

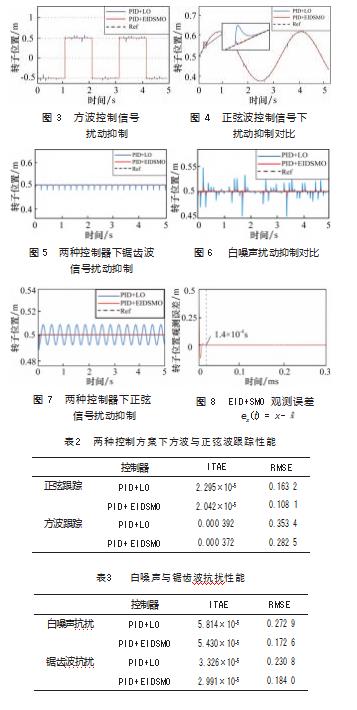
　　控制跟踪和抗干扰性能对比仿真结果分别如图3~7所示，方波控制信号可以看出PID+EIDSMO在不牺牲控制性能前提下，具有更快的扰动后收敛能力，在白噪声扰动中，抗扰性能更加显著，且如表2、表3所示ITAE和RMSE两项性能指标也有所提升。

　　相较与PID与普通龙伯格观测器，图8所示观测误差能在初始状态相差0.5 m情况下，能以较快速度收敛至零，且综上仿真结果PID+EIDSMO方法具有更好的抵抗外部干扰性能。

　　4结束语

　　本文针对高速旋转的的悬浮转子安全稳定性问题，研究了在外部未知扰动影响下的磁悬浮轴承系统转子位置偏移的控制问题。为了在不牺牲控制系统的控制鲁棒性以及系统响应速度的前提下提高整个系统的抗外部未知干扰能力，提出了一种基于等价输入干扰滑模观测器的比例积分控制方法。

　　通过等价输入干扰滑模观测器实时观测系统的运行状态变化，并将外部干扰观测出来并前馈到输入端，实现了主动磁悬浮轴承系统在扰动影响下的位置跟踪控制并抵消干扰的大部分影响。仿真结果表明，与传统的观测设计方法如Luenberger观测器相比，基于EID估计器的滑模观测器具有更小的观测误差，收敛速度快。并且相较于PID加传统龙伯格观测器控制方法，基于等价输入干扰估计器的滑模观测器的观测与控制方法对扰动具有更好的抑制效果，系统鲁棒性也进一步提升。

　　参考文献：

　　[1]崔晨.低摩擦损耗超导磁轴承[J].稀土信息,1992(3):13.

　　[2]詹三一,唐跃进,李敬东,等.超导磁悬浮飞轮储能的基本原理和发展现状[J].电力系统自动化,2001(16):67-72.

　　[3]国家电网公司"电网新技术前景研究"项目咨询组.大规模储能技术在电力系统中的应用前景分析[J].电力系统自动化,2013,37(1):3-8.

　　[4]周林,黄勇,郭珂,等.微电网储能技术研究综述[J].电力系统保护与控制,2011,39(7):147-152.

　　[5]张文亮,丘明,来小康.储能技术在电力系统中的应用[J].电网技术,2008(7):1-9.

　　[6]Y Altintas,S D Merdol.Virtual high performance milling[J].Cirp Annals,2007,56(1):81-84.

　　[7]Erhan Budak,A Tekeli.Maximizing chatter free material removal rate in milling through optimal selection of axial and radial depth of cut pairs[J].Cirp Annals,2005,54(1):353-356.

　　[8]Shin Shiung Yu,Shing Jen Wu,Tsu Tian Lee.Application of neu⁃ral-fuzzy modeling and optimal fuzzy controller for nonlinear magnetic bearing systems[C]//Proceedings 2003 Ieee/asme Inter⁃national Conference on Advanced Intelligent Mechatronics(aim 2003):IEEE,2003:7-11.

　　[9]K Nonami.Robust control of magnetic bearing systems by means of sliding mode control[C]//Proceedings of the Third International Symposium on Magnetic Bearings,1992.

　　[10]RB Zmood,Yuhong Jiang.Decentralised neural network control of magnetic bearings[C]//Proceedings of 1996 Canadian Confer⁃ence on Electrical and Computer Engineering:Ieee,1996:257-260.

　　[11]汤亮,陈义庆.磁悬浮系统的建模与不平衡振动自适应控制(英文)[J].Chinese Journal of Aeronautics,2007(5):434-442.

　　[12]Se Young Yoon,Long Di,Zongli Lin.Unbalance compensation for AMB systems with input delay:An output regulation ap⁃proach[J].Control Engineering Practice,2016,46:166-175.

　　[13]Shyh Leh Chen,Shyu Yu Lin,Chow Shing Toh.Adaptive unbal⁃ance compensation for a three-pole active magnetic bearing sys⁃tem[J].Ieee Transactions on Industrial Electronics,2019,67(3):2097-2106.

　　[14]江峰,吴华春,张丽,等.基于影响系数法的磁悬浮转子不平衡补偿控制[J].数字制造科学,2020,18(3):158-163.

　　[15]Sarah K Spurgeon.Sliding mode observers:a survey[J].Interna⁃tional Journal of Systems Science,2008,39(8):751-764.

　　[16]胡文金,周东华.基于输入等价干扰的DC-DC变换器自适应控制[C]//第二十七届中国控制会议,2008:1720-1724.

　　[17]方明星.基于等价输入干扰补偿的建筑结构抗震主动控制[D].长沙:中南大学,2010.

　　[18]贺志忠,郑景轩.等价输入干扰法在液压系统中的应用[J].科技创新导报,2010(14):87-88.

　　[19]纪志成,常军.基于等价输入干扰估计器的永磁同步电机无速度传感器控制[J].仪器仪表学报,2009,30(10):2139-2143.

　　[20]方明星,吴敏,佘锦华.基于等价输入干扰补偿的高精度速度控制[C]//第二十七届中国控制会议,2008:2377-2381.

　　[21]王军晓,陈林杰,俞立.基于等价输入干扰滑模观测器的磁悬浮球系统模型预测控制[J].控制理论与应用,2021,38(1):137-146.

　　[22]陈林杰.基于扰动补偿的磁悬浮球系统模型预测控制方法研究[D].杭州:浙江工业大学,2021.

　　[23]郁春江,谷瑞,杨洋.磁悬浮轴承控制系统的模型与参数优化[J].轴承,2020,489(8):37-43.

　　[24]Junxiao Wang,Lei Zhao,Li Yu.Adaptive terminal sliding mode control for magnetic levitation systems with enhanced distur⁃bance compensation[J].IEEE Transactions on Industrial Elec⁃tronics,2020,68(1):756-766.