摘要：由于直齿锥齿轮在传动过程中包含齿面摩擦和齿侧间隙等多种时变因素，导致轮齿间不可避免地发生振动冲击，影响传动平稳性及精度。为了提升锥齿轮的性能，研究直齿锥齿轮传动系统的非线性动力学特性，采用集中参数法建立了含齿面摩擦、齿侧间隙、综合传动误差等非线性因素的直齿锥齿轮轮传动系统弯扭轴耦合非线性动力学模型。使用4阶变步长Runge-Kutta法对直齿锥齿轮传动系统动力学微分方程进行仿真求解。通过分岔图、相图、Poincaré映射图分析系统的非线性动力学特性。结果表明：系统运行的过程中会发生跳跃分岔和擦边分岔使系统的运动轨迹和模式发生变化，并且出现连续的倍化分岔，使系统从周期1运动转迁为混沌运动；啮合阻尼比的增大会导致混沌运动逐渐变化为稳定的单周期运动；在动态设计系统时，适当提高啮合阻尼比可以提升系统的运行平稳性和可靠性。

　　关键词：直齿锥齿轮；齿面摩擦；非线性；分岔

　　0引言

　　锥齿轮传动系统具有改变传动方向、结构紧凑、运行平稳等特点，被广泛应用于航空航天、精密机床、工业机械臂等动力传动装置。由于锥齿轮在传动过程中包含齿面摩擦和齿侧间隙等时变因素，这就导致轮齿间不可避免的发生振动冲击，影响传动平稳性。随着对锥齿轮传动系统的性能要求不断提高，如何减少齿轮副冲击振动和噪声是保持锥齿轮传动系统稳定运行的关键所在。因此，对含齿面摩擦等多种时变因素的螺旋锥齿轮传动系统的冲击特性进行非线性动力学分析十分必要。王三民等[1]建立了8自由度锥齿轮传动系统动力学模型，并分析了系统分岔特性和运动规律。Yassine等[2]建立了故障锥齿轮系统模型，分析其动力学特性，并与正常锥齿轮系统的动力学特性进行对比。田亚平等[3]采用改进的CPNF法对直齿锥齿轮系统进行求解，研究了直齿锥齿轮系统周期运动及参数相互耦合转迁关系。林何等[4]建立了12自由度的并车弧齿锥齿轮系统非线性动力学模型，并分析了不同参量下系统的稳态特性。李春洋等[5]通过简化同步锥齿轮系统，分析了3种不同碰撞力模型，并得到了其动力学响应。李菲菲等[6]提出了一种计算直齿锥齿轮的啮合刚度的计算方法。莫帅等[7]建立了含轴承的单级面齿轮模型，研究了分流级和汇流级的不同非线性特性。林腾蛟等[8]建立了以锥-平行轴-行星多级齿轮传动系统，研究了其非线性振动特性。

　　本文以直齿锥齿轮传动系统为研究对象，考虑齿面摩擦及齿侧间隙等多种时变非线性因素，建立7自由度直齿锥齿轮非线性动力学模型，通过定义不同的Poin⁃caré截面，之后对系统动力学模型进行数值求解，研究啮合频率和啮合阻尼比对系统啮合状态和动态特性的影响，为系统参数设计和优化提供理论依据。

　　1动力学模型

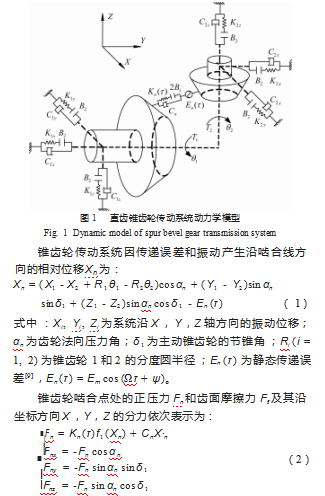
　　1.1直齿锥齿轮模型及受力分析

　　为了提升直齿锥齿轮传动系统动力学模型的准确性，将系统等效处理为主、被动轮沿3个坐标方向的振动，考虑含齿侧间隙和轴承支承，建立了8自由度的直齿锥齿轮传动系统动力学模型，如图1所示。图中，角标1和2分别表示主动锥齿轮和从动锥齿轮，两锥齿轮的轴线正交。θi（i=1，2）分别为主从动齿轮的扭转角位移。支撑两个锥齿轮的滚动轴承被等效为线性弹簧和线性阻尼，其在X，Y，Z坐标方向上支撑刚度系数分别表示为Kix，Kix，Kiz（i=1，2），支撑阻尼系数分别表示为Cix，Cix，Ciz（i=1，2）。2B 1为齿侧间隙，B2为轴承间隙，Kn(τ)是齿轮副的时变啮合刚度，Cn为齿轮副的啮合阻尼，En(τ)为齿轮副传动过程中产生的综合传动误差。Ti（i=1，2）分别为作用于主动锥齿轮和从动锥齿轮上的扭矩。

　　因此，通过适当提高系统的啮合阻尼比，可以有效减少系统原本存在的混沌运动，让系统回归周期运动减少轮齿发生的冲击振动，而且保证了齿轮副啮合传动的稳定运行，使系统的啮合精度和性能得到进一步的提高，从而满足更高的行业需求。

　　3结束语

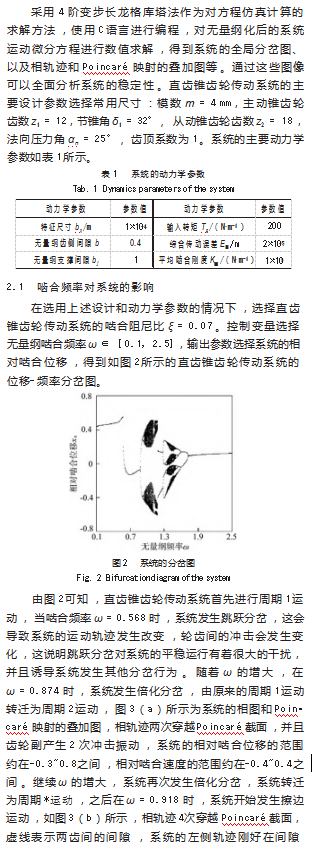
　　本文对直齿锥齿轮展开了受力分析，建立了含齿面摩擦、齿侧间隙等多种非线性因素的直齿锥齿轮传动系统非线性动力学模型和无量纲微分方程，采用4阶变步长龙格库塔法对方程进行了数值求解，分析了不同啮合频率和啮合阻尼比下系统的非线性动力学特性，主要结论如下。

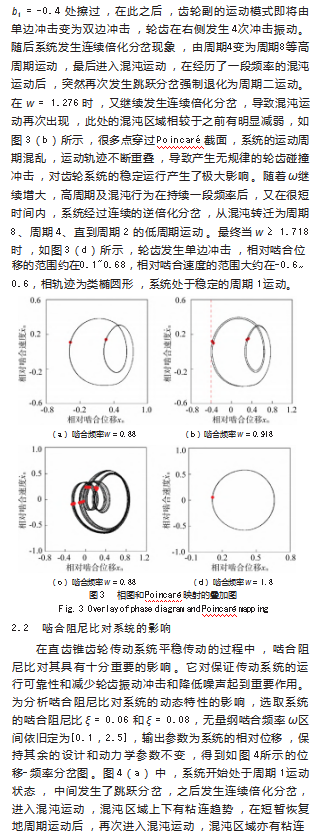
　　（1）随着ω的增大，系统首先经历了跳跃分岔，改变了系统的相轨迹；通过擦边分岔，使单边冲击变为双边冲击；以及连续倍化分岔使系统快速进入周期2运动、周期4运动、周期8运动和混沌运动，然后通过连续逆倍化分岔退化为稳定的周期1运动。

　　（2）当啮合阻尼比ξ减小时，系统的混沌区域增大，区域间发生粘连现象；当啮合阻尼比ξ提高时，系统的混沌消失，回归为低周期运动，最终保持周期1稳定运行。合理提高齿轮副的啮合阻尼比ξ,可以有效减少系统在混沌区域的复杂行为，增加系统的运行平稳性和可靠性，减少齿轮间的冲击振动及噪声。

　参考文献：

　　[1]王三民,沈允文,董海军.含间隙和时变啮合刚度的弧齿锥齿轮传动系统非线性振动特性研究[J].机械工程学报,2003(2):28-32.WANG S M,SHEN Y W,DONG H J.Nonlinear dynamical char⁃acteristics of a spiral bevel gear system with backlash and time-varying stiffness[J].Chinese Journal of Mechanical Engineering,2003(2):28-32.

　　[2]Yassine D,Ahmed H,Lassaad W,et al.Effects of gear mesh fluc⁃tuation and defaults on the dynamic behavior of two-stage straight bevel system[J].Mechanism and Machine Theory,2014,82:71-86.

　　[3]田亚平,杨江辉,王瑞邦.直齿锥齿轮分岔脱啮特性参数解域界结构[J].应用数学和力学,2023,44(8):965-976.

　　TIAN Y P,YANG J H,WANG R B.Parametric solution domain structures for bifurcation and non-meshing dynamic characteris⁃tics of straight bevel gear systems[J].Applied Mathematics and Mechanics,2023,44(8):965-976.

　　[4]林何,洪灵,江俊,等.受激并车弧齿锥齿轮系统两参量平面上解域界结构[J].振动工程学报,2021,34(5):1020-1026.

　　LIN H,HONG L,JIANG J,et al.Solution domain structures of power combining spiral bevel gear system under excitations in two-parameter plane[J].Journal of Vibration Engineering,2021,34(5):1020-1026.

　　[5]李春洋,张伟.含间隙同步锥齿轮锁定后的非光滑动力学分析[J].动力学与控制学报,2015,13(6):437-442.

　　LI C Y,ZHANG W.Kinetic analysis of non-smoothafter the syn⁃chronous straight bevel gears with clearance being locked[J].Journal of Dynamics and Control,2015,13(6):437-442.

　　[6]李菲菲,董惠敏,张楚.考虑齿对耦合的直齿锥齿轮啮合刚度计算方法[J].机械传动,2023,47(12):53-59.

　　LI F F,DONG H M,ZHANG C.Meshing stiffness calculation of spur bevel gears considering the tooth pair coupling[J].Journal of Mechanical Transmission,2023,47(12):53-59.

　　[7]莫帅,黄祖瑞,刘翊恒,等.航空非正交偏置面齿轮分汇流系统非线性动力学[J].力学学报,2024,56(4):1110-1122.

　　MO S,HUANG Z R,LIU Y H,et al.Non-linear dynamics of aeronautical non-orthogonal offset gear split flow system[J].Chi⁃nese Journal of Theoretical and Applied Mechanics,2024,56(4):1110-1122.

　　[8]林腾蛟,王丹华,冉雄涛,等.多级齿轮传动系统耦合非线性振动特性分析[J].振动与冲击,2013,32(17):1-7.

　　LIN T J,WANG D H,RAN X T,et al.Coupled nonlinear vibra⁃tion analysis of a multi-stage gear transmission system[J].Jour⁃nal of Vibration and Shock,2013,32(17):1-7.

　　[9]李润方,王建军.齿轮系统动力学—振动、冲击、噪声[M].北京:科学出版社,1997.

　　[10]机械设计手册编委会.机械设计手册.齿轮传动:单行本[M].4版.北京:机械工业出版社,2007.

　　[11]陈思宇,谭儒龙,郭晓冬.直齿锥齿轮啮合刚度计算方法研究[J].机械传动,2021,45(9):62-67.

　　CHEN S Y,TAN R L,GUO X D.Research on calculation meth⁃od of meshing stiffness of straight bevel gear[J].Journal of Me⁃chanical Transmission,2021,45(9):62-67.

　　[12]高建设,崔秉奇,丁顺良,等.齿轮-轴承传动系统擦边碰撞的动力学特性分析[J].振动与冲击,2022,41(13):1-7.

　　GAO J S,CUI B Q,DING S L,et al.Dynamic characteristics analysis of grazing impact of gear-bearing transmission system[J].Journal of Vibration and Shock,2022,41(13):1-7.

　　[13]杨艳.双参数空间内两级齿轮传动系统的动态响应[J].机械设计,2023,40(10):33-41.

　　YANG Y.Dynamic response of two-stage gear transmission sys⁃tem in dual parameter space[J].Journal of Machine Design,2023,40(10):33-41.

　　[14]李晓贞,苏阔,李同杰,等.考虑陀螺效应的面齿轮振动特性分析[J].噪声与振动控制,2023,43(2):58-63.

　　LI X Z,SU K,LI T J,et al.Analysis of face gear vibration char⁃acteristics considering gyroscopic effect[J].Noise and Vibration Control,2023,43(2):58-63.

　　[15]常乐浩,袁冰,宋文,等.齿轮副非线性接触特性与动力学耦合分析方法[J].西安交通大学学报,2022,56(10):1-10.

　　CHANG L H,YUAN B,SONG W,et al.A model for coupling analysis of the nonlinear contact characteristics and dynamics of gear pairs[J].Journal of Xi′an Jiaotong University,2022,56(10):1-10.

　　[16]孙宇梦,陈长征,张磊,等.考虑波纹度激励的齿轮系统动态特性研究[J].机械设计与制造,2024(1):79-84.

　　SUN Y M,CHEN C Z,ZHANG L,et al.Study on dynamic char⁃acteristics of gear system with waviness[J].Machinery Design&Manufacture,2024(1):79-84.

　　[17]王铎.摩擦条件下故障齿轮非线性振动特性分析[D].沈阳:沈阳工业大学,2023.

　　[18]张旭东,张磊,杨林杰,等.啮合阻尼对人字齿行星齿轮传动系统均载特性影响分析[J].机床与液压,2022,50(11):167-171.ZHANG X D,ZHANG L,YANG L J,et al.Analysis of the influ⁃ence of meshing damping on load sharing characteristics of her⁃ringbone planetary gear transmission system[J].Machine Tool&Hydraulics,2022,50(11):167-171.

　　[19]韩修静,黄启旭,丁牧川,等.谐波齿轮系统的快慢振荡机制研究[J].力学学报,2022,54(4):1085-1091.

　　HAN X J,HUANG Q X,DING M C,et al.A study of dynamical mechanisms of the fast-slow oscillations of harmonic gear sys⁃tem[J].Chinese Journal of Theoretical and Applied Mechanics,2022,54(4):1085-1091.

　　[20]银奎帮.齿轮传动系统的非线性振动及控制[D].兰州:兰州交通大学,2022.

　　[21]张建文.多间隙人字齿行星传动系统非线性频响分析[D].西安:西安工业大学,2021.