摘要：近年来，移动机器人领域中的仿生足机器人成为研究热点。其中，四足机器人由于移动速度快、动作灵活等优点被广泛研究与应用。但是，在实现足式机器人能够行走运动的同时，足底打滑、足端速度不一致等现象导致整个机器人机体的稳定性与航向控制依然存在问题。单纯依靠运动学对位置和轨迹进行控制和优化效果并不理想。为解决此问题，使用虚拟模型控制方法，由虚功原理简化了四足机器人的运动模型。同时将位姿变换指令转化为腿部关节的力矩指令，实现整机控制。在不同的阻尼系数和刚度系数下探究机体的足端轨迹、偏航距离和质心高度的变化，并对机体的偏航位移和偏航角度进行分析。经过计算与仿真实验，在合理的刚度系数和阻尼系数条件下，机器人的行进和偏航距离与足端轨迹得到了改善，机身航向与机体稳定性也得到了极大的提升。
       关键词：四足机器人；虚拟模型控制；机身航向；稳定行走控制

　　0引言

　　近年来，仿生足式机器人已经成为移动机器人领域中的热点研究课题[1]。相比起轮式和履带式机器人，足式机器人有着极大的灵活性和适应性[2]。从稳定性、操控性和制造成本3个角度，Hirose[3]认为足式机器人的最佳选择是四足机器人。通过对足式机器人足端轨迹规划控制，可以使其实现了简单的行走运动。但是这种单纯基于运动学模型，通过设计机器人足端周期性运动的轨迹，更侧重于机器人的腿部，而不是整个机体的运动控制。虽然对足端轨迹进行优化能够使机器人的机体在运动过程中相对更加的稳定，但是机器人在支撑相和摆动相周期内，不同腿足端的速度很难保证完全一致，往往会出现处于支撑相的腿或处于摆动相的腿无法同时支撑或摆动，导致行走时偏离原来的方向以及足底滑动现象。因此，采用控制方法来增强四足机器人在行走过程中的稳定性是十分必要的。

　　McGhee[4]设计了重心投影法，通过控制机器人的重心投影始终处于机器人支撑足的连线构成的支撑多边形内部，保证机器人的静态稳定。这种方法可以让机器人在行走过程中不会摔倒，但是运动过程十分缓慢，并且只适用于平坦地形上行走。Vukobratovic将零力矩点理论应用于四足机器人运动控制中，通过控制作用于机器人机身所有力的合力所产生的力矩，使其在地面上投影的分量为0，则能够保证机器人在运动时的动态稳定平衡，但在四足机器人的实际运动中，无法时刻满足零力矩要求[5]。

　　模型预测控制具有很好的跟踪性能和抗干扰能力[6]。黄烨等[7]将MPC控制引入了四足机器人的行走控制中，通过MPC控制实现了四足机器人足端落地点位置以及足底力的控制。但MPC控制器需要进行大量的求解计算，这可能导致控制延迟，特别是在实时性要求较高的系统中[8]。

　　跟随人工智能的逐步发展，如神经网络、强化学习等各种智能算法应运而生[9]。用智能算法来进行机器人的控制，不需要建立精确的机器人模型，而是通过大量的数据训练，进行不断地学习和试错，从而找到一种满足机器人机身稳定状态的控制方法。王文明[10]利用BP神经网络通过样本训练实现对机器人的运动控制和避障控制。吴磊[11]利用强化学习算法PPO策略、A2C策略和DDPG策略，均完成了四足机器人Trot步态下运动的任务，并且通过对比，证明了强化学习控制的有效性；Je⁃min Hwangbo[12]设计了一种改进的神经网络控制方法[13]，使得机器人拥有抗干扰力和环境适应力。智能算法在控制领域中展现出了强大的潜力，但其存在对训练数据要求高、模型解释性差等缺点。

　　目前，“虚拟模型控制”（Virtual Model Control，VMC）[14-15]是四足机器人主流的运动控制方法之一。虚拟模型控制方法控制结构简化、计算量较少，具有较强的抗扰能力[13]。本文采用虚拟模型控制方法将工作空间中的期望速度和位移，根据虚功原理转化成为机器人各关节的力矩，简化了四足机器人运动模型。对机器人的机体姿态，以及行进速度综合考虑，把高层的四足机器人位姿变换的指令转变为下层的腿部各关节的力矩指令，实现对机器人整个机体的控制。基于虚拟模型控制理论，实现对四足机器人的稳定行走控制。

　　1虚拟模型控制原理

　　虚拟模型控制（Virtual Model Control）由Pratt在1997年提出[16]。原理是利用不存在的假想元件，在机构作用力的受力点与外界环境之间建立关系，计算所受的虚拟力以及虚拟转矩，使机器人实现期望的运动[17]。

　　足端受力与关节力矩之间具有映射关系[18]，此关系由机器人的机械结构决定，通过机器人的正运动学模型得到足端相对于机器人腿部侧摆关节坐标系的位置信息，得到足端工作空间与关节空间的映射关系：

　　x=f(q)（1）式中：x=[x 1,x2,…,xn]，为机器人的机体足相对于空间的位姿向量；q=[q 1,q2,…,qm]，为关节空间的位置向量。

　　进一步求得x对q的偏导数，得
       
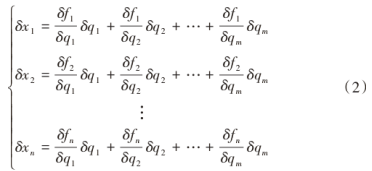
        即：
     

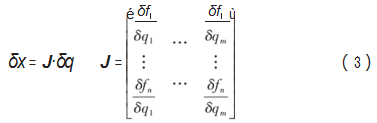
　　根据虚功原理τTδq+(-F)Tδx=0，联立上式，得

　　τ=JTF（4）

　　式中：τ∈Rn×1，为关节力矩向量；F∈Rn×1，为外界环境下的作用力；J∈Rn×m，为速度Jacobian矩阵，它表示将关节空间下的角速度值，转换为足端的速度值。J矩阵随着机器人关节角q不断变化。

　　四足动物在行走和奔跑运动过程中，足端抬起的高度，轨迹并不需要非常严格的限制。虚拟模型控制能够将四足机器人复杂的运动模型进行简化，把高层机体姿态变换的命令转变为各腿部关节的底层力矩控制，从而控制机器人的运动状态。此控制方法能够简单直接地反映机器人的运动状态，有效地实现机器人与外界环境之间的交互，保持机体状态的稳定[19]。

　　足式机器人进行控制时，采用弹簧元件和阻尼元件作为控制的虚拟构件，虚拟力计算的基本公式如式（5）所示。

　　Fu=B(d-)+K(ud-u)（5）

　　式中：Fu为虚拟构件产生的虚拟力；B为阻尼系数，K为刚度系数；ud和d表示足端的期望位置坐标和速度；u和表示实际的位置坐标和速度。

　　由于控制方法本身的特点，那么它在对足式机器人的运动控制过程中必然会带来控制误差。在简化机器人模型进行计算的假设条件下得到的各关节期望力矩，还要考虑用来补偿系统的惯性、离心力、结构件之间的摩擦等系统原本存在的复杂因素影响，因此最终完成的运动效果与理想的效果会有差异。通过对控制模型中阻尼系数和刚度系数的合理选取调整，可以使得差异变小，接近目标状态，就能完成足式机器人的稳定行走控制，发挥该算法简单、效率高的优势。

　　2腿部虚拟模型控制

　　以右前腿为例，由文献[20]中推导得到的四足机器人足端在侧摆关节处的坐标位置坐标表示为：

　　最终可以确定四足机器人的右前腿足端正运动学方程为：
      

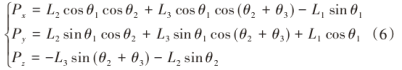
　　对3个方向的坐标分别求3个关节角度的偏导数，得到了四足机器人右前腿的Jacobian矩阵：
      

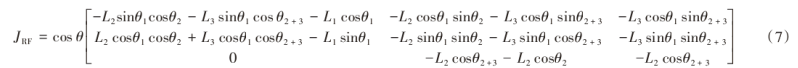
　　当腿部处于支撑相时，在x，y，z三个方向上的虚拟力计算：
      

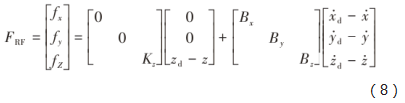
　　当腿部为摆动相时：
        

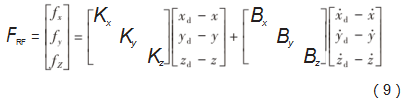
　　式中：Kx、Ky、Kz为3个方向上的刚度系数；Bx、By、Bz为阻尼系数；xd、yd、zd为足端轨迹在3个方向的期望坐标，x、y、z为足端位置的实际坐标值。

　　最终由构建的3个平动方向的虚拟力，利用式（4）得到作用于机器人腿部3个关节的期望关节力矩，实现机器人的平动行走运动。

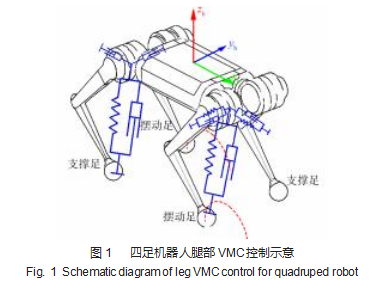
　　图1为四足机器人腿部VMC控制示意图。

　　3机身航向控制

　　四足机器人在实际的行走过程中，不会持续进行直线运动，因此除了平动运动外，还需要考虑机器人的转向运动。

　　F′为支撑相在3个方向上的虚拟力：
      

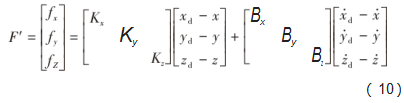
　　四足机器人的行进方向通过航向角来调整（图2），可以通过在质心绕z轴的位置添加1组虚拟构件，产生1个虚拟转矩来调整机器人的航向角。

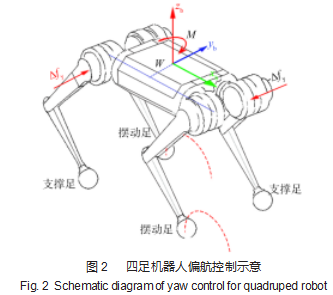
　　控制航向角的虚拟转矩的公式为：

　　Mψ=Kψ(ψd-ψ)+Bψ(ψ̇d-ψ̇)（11）

　　式中：ψd和ψ为期望的航向角度和实际的航向角度；ψ̇d和ψ̇为期望的航向角速度和实际的航向角速度，ψd和ψ̇d由上层控制指令给出；ψ和ψ̇为实际测量得到的机身航向角度。

　　在行进过程中，机体转向的力由处于支撑相的两条腿产生。当需要转向时，使处于支撑相的两条腿产生侧向支撑力，两个支撑力大小相等，方向相反，一是可以保证机体总的侧向力保持不变；二是这两个作用力在机器人的头部和尾部施加两个方向相反的力，可以实现机体绕质心旋转，利用侧向力来求出该转向转矩，实现机体的转向控制。产生的机体侧向虚拟力变化量表示为Δfy。

　　Δfy=(Kψ(ψd-ψ)+Bψ(ψ·d-ψ·))/W（12）

　　式中：W为机器人质心到侧摆关节的横向距离。

　　通过两侧支撑腿作用在侧摆关节上的侧向作用力转化作用于质心的转向力矩，能够让机器人按照给出的期望航向角度行走。当机器人的上层控制器给定的航向角度和角速度按照时间规律变化时，机器人则能够执行转向运动。此时支撑足所受虚拟力为：
       

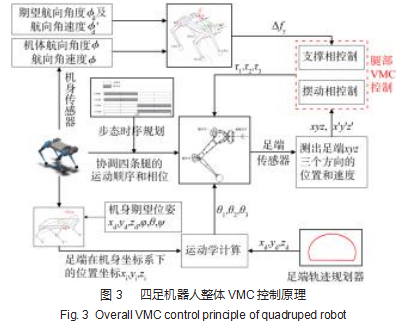
　　将上述章节中的四足机器人机身姿态变换控制以及步态规划，与四足机器人腿部VMC控制结合起来，实现四足机器人的整体VMC控制。图3所示为四足机器人整体VMC控制原理。

　　在运动过程中，如果机器人上层控制给出的期望航向角较大，使得在转向过程中，机器人为了快速跟踪，瞬时航向角速度过大，机器人关节转角太大，超出关节限位，导致机体失稳，发生侧翻。为了避免出现此状况，需要对机器人的航向角速度进行约束，使ψmin≤ψ≤ψmax。

　　4仿真实验与分析

　　在MATLAB/Simulink仿真环境中，进行仿真实验的验证。在Simulink仿真平台中完善仿真框架，并且封装为各部分控制模块，完善机器人的仿真模型。

　　对于在运动控制过程中，刚度系数K和阻尼系数B的选择是机器人运动的关键，增益过高，作用在机器人关节上的力矩太大，机器人刚性过高，无法稳定运动；增益太小，各关节的力矩较小则无法支撑机器人的机体。在行走过程中，机器人腿部会有打滑的现象发生。因此需要通过仿真实验，比较不同系数下，前进和偏航距离，以及足端轨迹形状，对刚度系数和阻尼系数进行合理的选择。            4.1阻尼和刚度系数对机体运动的影响

　　（1）阻尼系数B

　　取3个方向上的刚度系数K均为2 000 N/m，阻尼系数B的取值范围为50~250 N/m，共5组。足端轨迹采用前面章节利用Bezier曲线方法规划的足端轨迹，足端轨迹中的步长值s取0.22 m，抬腿高度h为0.13 m，步态周期T为0.5 s。四足机器人初始姿态中偏航角ψ,俯仰角θ,横滚角φ均设置为0 rad，机体的高度为0.35 m。

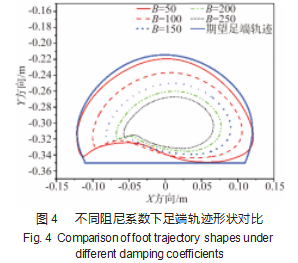
　　足端轨迹形状如图4所示。可以看出，阻尼较小时，足端轨迹的形状与所规划的轨迹相差不大；随着阻尼系数B越大，在实际行走过程中，机器人的足端轨迹变化振幅逐渐减小，振幅趋于稳定，但是足端轨迹与所规划的理想足端轨迹形状差距更大。

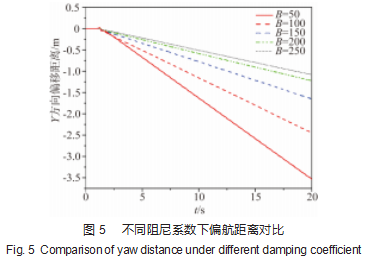
　　对机器人偏航距离进行观测，结果如图5~6所示。从图5可以看出，阻尼系数B为50 N/m时，机体偏航情况严重，机体在一开始运动时所受翻转力矩也更大，不能很好地完成直线运动；随着阻尼系数B变大，偏航情况也变好，并且变化振幅逐渐稳定下来。

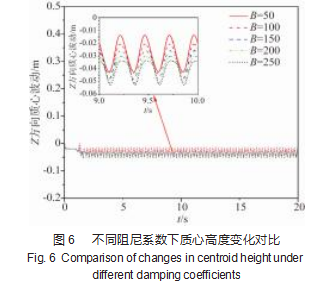
　　（2）刚度系数K

　　在阻尼系数B为100 N/m的情况下，取刚度系数K的取值范围为800~3 200 N/m，共6组。其余的条件不变，进行仿真，得到实验数据如图7~9所示。

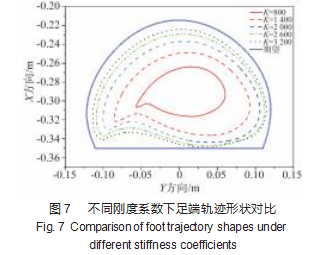
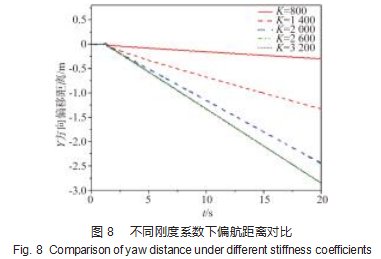
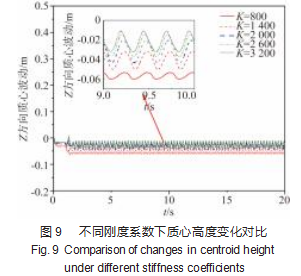
　　从图7中可以观察到，增大刚度系数，物体弹性特性增强，振幅变大，能够使机器人足端轨迹很快地跟踪到理想的期望轨迹；之后继续增大刚度系数，在与阻尼系数的配合下，实际足端轨迹与理想足端轨迹之间的偏差会逐渐减小，并且趋于稳定。

　　对于刚度系数K与阻尼系数B的分析得知，为了使机体的实际足端轨迹与理想足端轨迹之间的偏差减小，足端轨迹快速跟踪上期望的理想轨迹，刚度系数取较大值；在直线平动运动时，y方向的刚度系数太大，会使机器人的腿部摆动时，其侧向产生位移，使机器人发生更大的偏航误差。为了减小机器人的偏航误差，y方向的刚度系数应取较小值，为了使侧向位移偏差快速稳定，阻尼系数取较大值。

　　最终选取在无偏航角控制下，机器人能够比较稳定运动的刚度系数和阻尼系数如下：
      

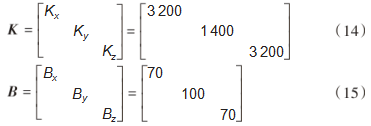
　　4.2机体航向控制实验

　　设置期望偏航角度为0 rad，仿真时间60 s，对机器人3个方向的位移进行分析，设置3个方向的刚度系数为3 200 N/m，阻尼系数100 N/m。结果如图10~11所示。

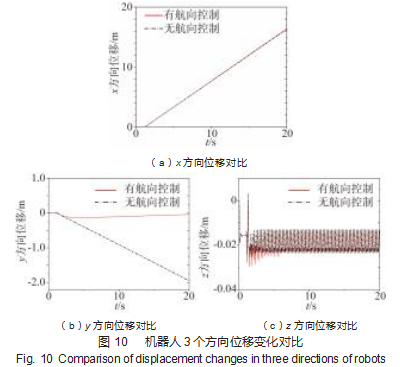
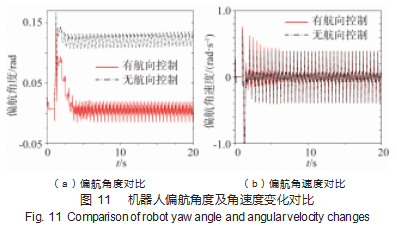
　　从图中可以看出，当期望航向角度设置为0 rad时，机器人在起步阶段，受机身翻转力矩的影响，机体发生偏航；在航向控制下，偏航角度减小，偏航角速度变化趋于稳定。而无航向控制时，机器人会依据误差造成的偏航角度继续运动，机器人机体在y方向的偏航位移相比无偏航控制时要更加小；质心高度的变化也更加小。当机器人偏航角度趋于稳定后，偏航角速度的变化相差不大。

　　设置航向角速度约束条件-0.5≤φ̇≤0.5，机器人行进速度为1.2 m/s，设置期望航向角：
      

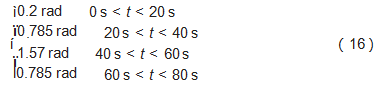
　　测试机器人连续转向的能力，仿真结果如图11~16所示。

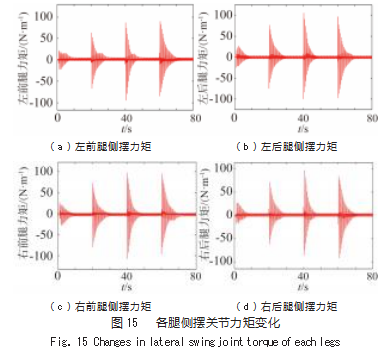
　　由图12~13可以看出，机器人能够按照期望航向角度完成连续运动，并且在偏航角速度约束范围内机体能够完成所要求的转向任务。由图14可以看出机体在运动过程时质心变化稳定，即使在转向过程中，机体的质心波动也不会很大，能够保证平稳运动。

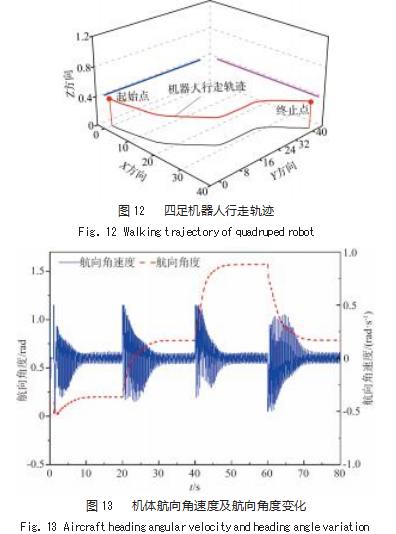
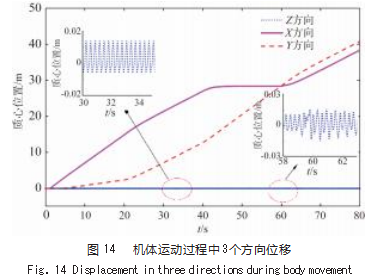
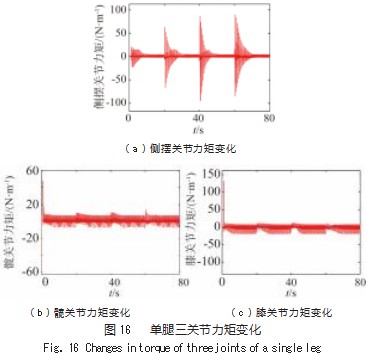
　　图15所示为机器人在转向运动过程中，机身四条腿侧摆关节所受力矩。运动过程中，4条腿的侧摆关节力矩变化均匀。图16为机器人单腿三关节所受力矩。在转向过程中，机体转向所需的力矩主要由侧摆关节提供，当完成转向后，侧摆关节力矩会稳定至一个较小值；髋关节、膝关节的关节力矩负责对机器人在直行方向的稳定行走。

　　5结束语

　　本文利用虚拟模型控制原理以及虚功原理，以机器人每个侧摆关节坐标系作为基坐标系，建立四足机器人腿部虚拟模型控制，通过对比在平动直线运动下不同参数对运动的影响，确定出运动效果较理想的增益参数；为解决机器人在运动时的航向控制问题，当机器人腿部处于支撑相时，利用目标航向角与航向角速度，实际航向角与航向角速度之间的误差关系，计算出机体在世界坐标系下转向所需要的侧向虚拟力，通过Jacobian矩阵计算，转换为各关节转向所需的关节力矩，实现了四足机器人的稳定行走与航向控制。

　　[1]葛卓.四足机器人稳定行走控制与参数优化研究[D].北京:北京理工大学,2020.

　　[2]白柳,罗金良,胡鹏飞,等.虚拟模型控制被动柔性脊柱四足机器人研究[J].机电工程技术,2022,51(3):202-206.

　　BAI L,LUO J L,HU P F,et al.Research on passive flexible spi⁃nal quadruped robot controlled by virtual model[J].Mechanical&Electrical Engineering Technology,2022,51(3):202-206.

　　[3]HIROSE S,KATO K.Study on quadruped walking robot in To⁃kyo Institute of Technology-past,present and future[C]//Proceed⁃ings 2000 ICRA.Millennium Conference.IEEE International Conference on Robotics and Automation.Symposia Proceedings,2000,1:414-419.

　　[4]MCGHEE R B,ISWANDHI G I.Adaptive locomotion of a multi⁃legged robot over rough terrain[J].IEEE Transactions on Sys⁃tems,Man,and Cybernetics,1979,9(4):176-182.

　　[5]王新,鄢沛峰.下肢穿戴式助行器步态规划与稳定性分析[J].机械传动,2023,47(12):82-88.

　　WANG X,YAN P F.Gait planning and stability analysis of lower limb wearable walkers[J].Journal of Mechanical Transmission,2023,47(12):82-88.

　　[6]谢嘉,皇小虎,李永国,等.基于故障估计的农机路径跟踪容错控制方法研究[J/OL].南京农业大学学报,1-15[2024-09-24].
       XIE J,HUANG X H,LI Y G,et al.Research on fault tolerant control method of agricultural machinery path tracking based on fault estimation[J/OL].Journal of Nanjing Agricultural University,1-15[2024-09-24].http://kns.cnki.net/kcms/detail/32.1148.s.20240612.1651.002.html.

　　[7]黄烨中.基于模型预测控制的足式机器人奔跑控制[D].长沙:国防科技大学,2022.

　　[8]贺庆,冀杰,冯伟,等.割草机器人自适应时域MPC路径跟踪控制方法[J].智慧农业(中英文),2024,6(3):82-93.

　　HE Q,JI J,FENG W,et al.Adaptive time horizon MPC path tracking control method for mowing robot[J].Smart Agriculture,2024,6(3):82-93.

　　[9]李杰,毕乃祥,李静.智能机器人多媒体信息融合平台研发及应用[J].工业控制计算机,2024,37(6):66-67.

　　LI J,BI N X,LI J.Research and application of an intelligent ro⁃bot&multimedia fusion platform[J].Industrial Control Comput⁃er,2024,37(6):66-67.

　　[10]王文明.四足机器人步态规划与运动控制研究[D].青岛:山东科技大学,2012.

　　[11]吴磊.基于深度强化学习的四足机器人步态分析[D].济南:山东大学,2021.

　　[12]SAKAKIBARA Y,KAN K,HOSODA Y,et al.Foot trajectory for a quadruped walking machine[C]//IEEE International Work⁃shop on Intelligent Robots and Systems,Towards a New Fron⁃tier of Applications.1990,1:315-322.

　　[13]朱晓璐.四足机器人外力扰动下的反应式控制策略研究[D].南京:南京理工大学,2023.

　　[14]BLEDT G.Regularized predictive control framework for robust dynamic legged locomotion[D].Massachusetts:Massachusetts Institute of Technology,2020.

　　[15]张国腾,荣学文,李贻斌,等.基于虚拟模型的四足机器人对角小跑步态控制方法[J].机器人,2016,38(1):**-74.

　　ZHANG G T,RONG X W,LI Y B,et al.Control of the quadrupe⁃dal trotting based on virtual model[J].Robot,2016,38(1):**-74.

　　[16]郑向歌,王凯.基于LQR参数整定的汽车路径跟踪控制方法研究[J].信息通信,2017(1):38-39.

　　[17]XUE J,SHEN B.A novel swarm intelligence optimization ap⁃proach:sparrow search algorithm[J].Systems Science&Control Engineering,2020,8(1):22-34.

　　[18]PRATT J,DILWORTH P,PRATT G.Virtual model control of a bipedal walking robot[C]//Proceedings of International Confer⁃ence on Robotics and Automation:Albuquerque,NM,USA:IEEE,1997,1:193-198.

　　[19]张政.云-边融合的四足机器人系统研究[D].南京:东南大学,2022.

　　[20]薛晨慷,李光,易静,等.基于Bezier曲线的四足机器人Trot步态优化[J].湖南工业大学学报,2022,36(5):42-49.

　　XUE C K,LI G,YI J,et al.Trot gait optimization of quadruped robots based on Bezier curves[J].Journal of Hunan University of Technology,2022,36(5):42-49.