摘要：以应用于气流纺的磁悬浮纺杯转子-轴承系统为例，建立了纺杯转子的动力学模型，基于Riccati传递矩阵法，对转子在轴承刚度为5×106 N/m时的3阶临界转速以及临界转速随轴承刚度的变化情况进行了计算分析，基于ANSYS13.0对上述纺杯转子-轴承系统进行了动力学仿真分析，并将仿真结果与Riccati传递矩阵法计算结果进行了对比，两者相对误差在5%以内。采用HP35670A频率响应分析仪分别对自由状态以及悬浮时的纺杯转子进行了模态试验，测出了转子在两种状态下的固有频率。整个转子-轴承系统的高速运转试验对转子在不同转速下磁浮轴承处的位移进行了统计分析，以达到对理论计算、仿真分析结果进一步验证的目的。结果表明：所建立的转子-轴承系统动力学模型是合理的，对柔性转子的设计与分析具有一定的参考意义。

　　关键词：磁悬浮纺杯转子；Riccati传递矩阵法；有限元法；试验模态分析

　　0引言

　　气流纺设备通过分梳辊将纤维条开松成单纤维，单纤维在气流的作用下进入高速回转的纺杯内壁，由于离心力的缘故滑入凝聚槽内聚集形成纱尾，同时被加捻成纱引出并绕成纱筒。与其他纺织技术相比，气流纺具有流程短、原料适用范围广以及效率高等优点，因此，气流纺设备的发展越来越受到人们的重视[1-2]。纺杯是气流纺设备的关键部件之一，它的速度与可靠性直接关系到纺纱的效率与纱的质量，如何在现有基础上进一步提高纺杯的转速成为纺纱设备领域研究的热点。磁悬浮轴承由于具有无摩擦、没有油润滑、刚度可调等优点，为提高纺杯转速与寿命提供了新的思路。

　　纺杯转子在工作时的转速极高，德国赐来福公司生产的Autocoro 360型及Autocoro 480的转杯转速达到了15万r/min，引出速度最高300 m/min。因此，对纺杯转子系统进行动力学分析，使转子的工作转速远离临界转速是十分必要的。目前，对于柔性转子-轴承系统的动力学分析主要采用传递矩阵法与有限元法。传递矩阵法的优点是矩阵的维数不随系统自由度的增大而增大，而且程序简单，所需贮存单元少，机时短[3-4]；有限元法需占用更多的计算机存储与机时，程序比较复杂，但是计算结果精度较高，划分的单元数目可以比传递矩阵法少，而且可以避免数值不稳定现象。

　　本文分别基于Riccati传递矩阵法和ANSYS 13.0对径向采取主动磁轴承、轴向采用永磁轴承的纺杯转子-轴承系统进行了分析，与模态试验的结果进行了对比验证，并采用带传动进行了高速运转试验。

　　1基于Riccati传递矩阵法的动力学分析

　　图1所示为磁悬浮纺杯转子-轴承系统结构简图，纺杯的设计转速为12万r/min。转子采取径向主动磁悬浮轴承与轴向永磁轴承相结合的支承方式，实现了转子的五自由度悬浮。这样的结构设计使得转子的装拆变得更加简单，可以从转子的大端方向直接取出。对磁悬浮纺杯转子系统采用传递矩阵法进行动力学分析之前，需要先对转子进行离散化，即沿轴线把转子简化为由若干具有转动惯量的集中质量和无质量弹性轴段组成的多自由度系统[5]；轴承用弹簧单元等效替代[6]。

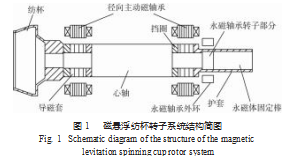
　　图1中转子中挡圈、导磁套及护套与转子以及护套与永磁体、固定棒等的配合均为过盈配合，各部分所用材料如表1所示。由于涉及到的配合均为过盈配合，故离散化时将心轴、永磁体及永磁体固定棒视为刚性连接；把导磁套、护套和挡圈等效成集中质量点，而不考虑其对转子本身刚度的影响；结点一般选在截面有突变处以及轴的端部等位置，结点的数目要根据转子的结构特点及尺寸参数合理确定。图2是纺杯转子-轴承系统离散化后的动力学模型，模型具有34个集中质量点，分为33个轴段，轴承简化为弹簧-阻尼单元。

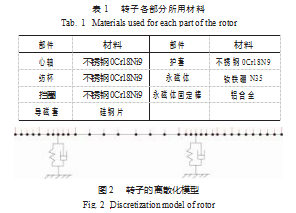
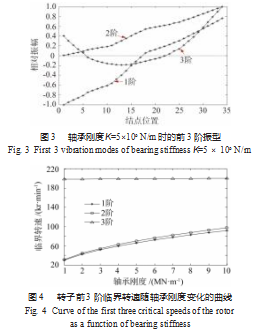
　　由于阻尼比较小，在计算低阶固有频率时，影响又不大[7]，这里假定阻尼c=0。根据转子的离散化模型，利用MATLAB编程即可实现转子-轴承系统的Riccati传递矩阵法计算。轴承刚度取K=5×106 N/m时，转子的前3阶临界转速分别为：nc1=66 180 r/min，nc2=69 943 r/min，nc3=199 420 r/min；对应的振型如图3所示，从图中可以看出前两阶为刚体摆动模态，第3阶为弯曲模态。图4是转子前3阶临界转速随轴承刚度变化的曲线，其中刚度的取值范围为（1～10）×106 N/m，随着刚度的增加，刚体模态对应的临界转速增加且变化较大，弯曲模态基本不变。由于纺杯转子的设计转速n=12万r/min，为使n满足条件：nc k<n<nc k+1，磁轴承的刚度应低于8×106 N/m。

　　2基于ANSYS的动力学仿真

　　ANSYS软件基于有限元法提供了一种计算和分析转子动力学问题的有效途径，并且计算精度更高，能够准确地模拟转子系统的质量和惯性，提供了大量能够模拟陀螺效应的单元[8]。下面基于ANSYS 13.0对上述纺杯转子-轴承系统进行了动力学仿真分析。

　　2.1转子系统动力学模型的建立

　　纺杯转子是一个装配体，建模之前先要根据转子的结构特点将转子划分为若干段，并计算出导磁套、挡圈及护套等效到各节点处的等效质量和等效转动惯量。与前述传递矩阵法一样，这里忽略导磁套及护套等对转轴刚度的影响，仅将其等效为具有转动惯量的集中质量；转轴使用BEAM188单元，不同轴段通过定义不同的梁截面形状来实现；轴承采用COMBIN214单元，COM⁃BIN214单元允许在平面内两个垂直的方向上定义刚度与阻尼特性，轴承的作用平面可以通过设置关键字来实现；等效后的集中质量用MASS21来模拟[9]。

　　建立模型时，在集中质量及轴承处设置节点；轴承单元的建立需要先创建两个节点，然后直接由节点生成COMBIN214单元；接着对集中质量单元进行定义和对轴进行网格划分，这样转子-轴承系统的有限元模型就建好了。图5所示为在ANSYS13.0中建立的纺杯转子系统动力学分析的有限元模型。

　　2.2纺杯转子-轴承系统的仿真分析

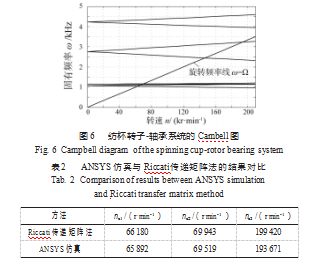
　　建立完模型后，就可以施加载荷与约束并进行转子动力问题的求解了。这里限制转子的轴向UX以及旋转ROTX两个自由度，约束轴承单元外围节点的所有自由度，求解时使用命令OMEGA指定转子的转速，使用命令CORIOLIS设置陀螺效应。转子动力学分析中可以使用DAMP和QRDAMP特征值求解器，考虑到阻尼对转子临界转速的影响较小，这里选用求解效率更高的QR⁃DAMP求解器[10]。图6所示为轴承刚度取5×106 N/m时仿真得到的坎贝尔（Cambell）图，图中旋转频率线ω=Ω与正向涡动频率曲线的交点即临界转速，前3阶分别为：nc1=56 196 r/min，nc2=69 384 r/min，nc3=185 306 r/min。相同刚度下，Riccati传递矩阵法与ANSYS仿真分析的结果对比如表2所示，从表中可以看出两种方法的分析结果差别很小，相对误差在5%以内。

　　3转子的试验模态分析及高速运转试验

　　3.1转子的模态试验分析

　　试验模态分析（Experimental Modal Analysis，EMA）是通过对转子进行人工激励，测量系统对输入（激励）与输出（响应）信号进行处理，得到频率响应函数，然后采用频域或时域的识别方法识别系统的固有频率、振型或阻尼比等参数。

　　本文试验采用HP35670A频率响应分析仪分别对自由状态下和悬浮时转子的固有频率进行了测定。试验中，加速度传感器在转子上的粘贴位置应选在激励响应较为明显的点，试验中加速度传感器贴在转子的末端。自由状态时，可选的力锤敲击点较多；悬浮时，由于转子中间绝大部分被轴承所封闭，力锤的敲击点只能是转子的两端。图7所示为自由状态和悬浮时的试验装置及频率特性曲线图。转子在自由状态下进行模态试验分析，得到的一阶固有频率即一阶弯曲模态为3 177 Hz；悬浮时，理论上可以得到转子-轴承系统包括刚体模态在内的所有模态，但在幅频特性曲线上刚体模态对应的幅值较小，再加上外界的干扰，很难准确地识别出转子-轴承系统的刚体模态，试验测得纺杯转子在悬浮时的一阶弯曲模态频率为3 233 Hz，略高于自由状态时的试验结果，且与传递矩阵法及ANSYS仿真结果相吻合。

　　3.2转子的高速运转试验

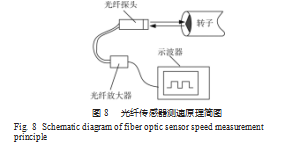
　　实际的气流纺设备中，纺杯的高速运转通过龙带驱动来实现。本试验中，纺杯转子由带传动实现高速转动。皮带选用尼龙片基带，其具有质轻、耐用、伸长小及耐磨性好等特点，因此适合高速传动；主动轮通过过盈配合装在电机轴端。皮带的另一端直接挂在纺杯转子上；试验中，转子以及电机的实际转速利用光纤传感器来测量，测速原理如图8所示，通过在带轮或转子端面标记黑色扇形弱反射面，转子转动的时候，光纤传感器的探头发出的光束交替照射在端面的黑色区域和剩余的强反射区域，传感器便输出强弱变化的矩形波电压信号，通过示波器分析矩形波的频率即可测得电机或转子的转动频率，整个试验装置如图8所示。

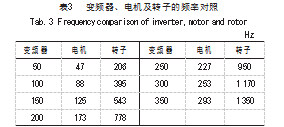
　　由于纺杯处于五自由度悬浮状态，所以所需的驱动功率较小，试验中所用电机为2极异步电动机，额定功率0.8 kW，额定转速为24 000 r/min，电机的调速通过变频器实现。带传动的传动比为i=4.8。试验中，变频器、电机及转子的频率对应关系如表3所示。

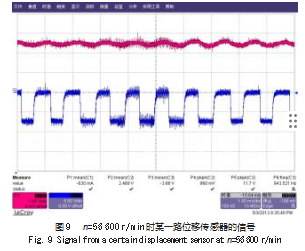
　　试验中对转子在不同转速下，磁悬浮轴承位移传感器和光纤测速传感器的信号进行了动态测量，试验发现：在低转速时，位移传感器的输出信号近似为直流；高速时出现与转速信号同频的正弦波，这主要是由于转子受自身的不平衡量激励而产生的。图9所示为转子在56 600 r/min时，其中一路位移传感器的输出信号和转速信号的波形图。试验装置中径向主动磁悬浮轴承的单边保护气隙为δ=0.05 mm，位移传感器输出0～5 V的电压信号，平衡位置时为2.5 V，设位移传感器输出信号波动的幅值为us，则转子涡动的幅值a=（0.05us/2.5）mm；转子转速n=56 600 r/min时，us约为0.3 V，转子涡动的幅值a=0.006 mm。

　　4结束语

　　传递矩阵法与有限元仿真法得到的临界转速与转子模态试验分析结果略有差异，这主要是由于转子动力学建模时作了一定的简化。高速转子设计时，可以根据需要灵活地选择使用传递矩阵法或是有限元法，同时应使工作转速避开临界转速，并保留一定的裕度。转子的不平衡会引起转子的挠曲与内应力，是旋转机械的主要激振源，对高速转子进行动平衡是十分必要的。

　参考文献：

　　[1]王善元,于修业.新型纺织纱线[M].上海:东华大学出版社,2007.

　　[2]秦贞俊.转杯纺纱技术的发展[J].国外纺织技术,2002(10):l-5.

　　[3]顾家柳.转子动力学[M].北京:国防工业出版社,1985.

　　[4]钟一谔,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1987.

　　[5]唐天国.基于传递矩阵法的船舶推进轴振动特性研究[J].舰船科学技术,2017,39(8):31-33.

　　TANG T G.Study on vibration characteristics of ship propulsion shaft based on transfer matrix method[J].Ship Science and Tech⁃nology,2017,39(8):31-33.

　　[6]徐园平.柔性转子磁悬浮轴承支承特性辨识[D].南京:南京航空航天大学,2018.

　　[7]王小东,王会良,苏建新.基于传递矩阵法的电主轴建模与实验分析[J].机床与液压,2022,50(4):13-18.

　　WANG X D,WANG H L,SU J X.Modeling and experimental analysis of motorized spindle based on transfer matrix method[J].Machine Tool&Hydraulics,2022,50(4):13-18.

　　[8]李克雷,谢振宇.基于ANSYS的磁悬浮转子的模态分析[J].机电工程,2008,25(1):1-3.

　　LI K L,XIE Z Y.Model analysis of the magnetic suspension rotor based on ansys[J].Mechanical&Electrical Engineering Maga⁃zine,2008(1):1-3.

　　[9]周瑾,蔡永飞.磁悬浮轴承-转子系统的理论与试验模态分析[J].武汉理工大学学报(信息与管理工程版),2010,32(6):889-891.

　　ZHOU J,CAI Y F.Theoretical and experimental modal analysis of active magnetic bearing-rotor test rig[J].Journal of Wuhan University of Technology(Information&Management Engineer⁃ing),2010,32(6):889-891.

　　[10]曹勤,徐龙祥.基于有限元的磁悬浮轴承支承转子的模态分析研究[J].机械工程师,2009(1):76-77.

　　CAO Q,XU L X.Research on the amb-system dynamics proper⁃ties caused by flexible foundation[J].Mechanical Engineer,2009(1):76-77.