摘要：针对当前机器人的运动情况复杂化、高速化，为保障运动时的安全性，提出一种基于任务空间约束的机器人轨迹规划算法。为分析任务空间约束对工业机器人轨迹规划的影响，采用DH参数法建立机器人模型，通过矩阵连乘得到运动学正解，获得基于机器人基坐标系的机器人末端位姿；通过代数法求解机器人逆运动学模型，得到机器人当前位姿下的各关节角度。人为设定软边界，并以圆弧轨迹为例，采用反向前瞻正向规划的方法对机器人末端进行速度规划。通过MATLAB仿真分析，对比无边界约束下的机器人轨迹规划算法和基于软边界实时监控的工业机器人轨迹规划算法对末端速度的影响。结果表明：在考虑软边界实时监控的情况下，机器人末端速度能够得到及时调整，在边界前平稳减速并停止，对优化工业机器人任务空间的轨迹规划算法具有参考意义。

      关键词：工业机器人；轨迹规划；自适应前瞻；边界约束

　　0引言

　　目前，机器人已被广泛用于各类型各行业的生产流程中，工业机器人已成为企业自动化、智能化升级的关键部件。在生产过程中，需要设定机器人的工作空间，以保证机器人在安全环境内工作，这既是为了防止机器人发生碰撞，也是为了保护工人。这种由用户自行设定的可变工业机器人工作空间限制称为软边界。

　　根据规划作业空间的不同，工业机器人的轨迹规划可分为关节空间规划和笛卡尔式空间规划。在笛卡尔式空间，即任务空间中的运动分为点到点运动和连续轨迹运动。点到点运动只关注起点和终点的位置和姿态，运动过程中不关注机器人末端轨迹，因此通常在关节空间进行轨迹规划，以实现更高效便捷的运动；连续轨迹运动以特定的控制点绘制出末端运动轨迹，如直线、圆弧等，并要求机器人末端按照轨迹进行运动。因此一般在任务空间进行轨迹规划后，再通过关节联动控制，保证末端以特定的轨迹运动。

　　本文以六自由度机器人为研究对象，根据MD-H参数法建立六自由度机器人运动学模型，并得到机器人MDH参数。根据MDH参数以及各个关节坐标系，建立每个关节的矩阵坐标系，通过坐标系变换矩阵连乘建立机器人正运动学模型，对于满足Pieper原则的机器人构型，采用代数解求解机器人逆运动学模型；以任务空间中的圆弧轨迹为例，进行无约束的机器人任务空间轨迹规划，再引入软边界实时监控，对机器人任务空间中的轨迹规划进行优化，研究基于软边界实时监控和任务空间约束下的轨迹规划对机器人运动连续性及变化的影响。

　　1机器人运动学建模

　　1.1 MDH模型建立

　　D-H机器人建模方法由Denavit和Hartenberg提出[11]；后来S.Hayatl修正提出MDH机器人建模方法，MDH模型与标准DH模型（SDH）的差别在于连杆坐标系的固定位置。SDH模型将连杆的坐标系固定在该连杆的输出端（下一关节），体现在坐标系Ωi-1与关节i对应，而MDH和则将坐标系固定在连杆的输入端（上一关节），体现在坐标系Ωi-1与关节i-1对应。同时两种建模方法的连杆坐标系变换规则也有差别，其中SDH是先围绕Z轴变化再围绕X轴变化，而MDH则刚好相反。在串联机器人的运动学研究中，SDH和MDH的差别不大，但是研究动力学时，MDH模型的表现形式将比SDH简洁清晰，涉及混联机器人时，SDH定义则存在歧义性。综合考虑，本文采用MDH建模的方法。

　　如图1所示，两个构件相连，中间关节轴线有两条公法线与其垂直，每条公法线对应一个连杆，如Zi分别与公法线ai-1和ai垂直。两公法线之间的夹角为转动角，记为θi，其转向按绕轴线Zi的右手螺旋法则确定。

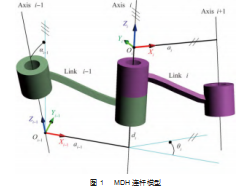
　　根据MDH建模得到机器人关节连杆参数如表1所示。

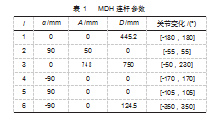
　　1.2运动学正解

　　以连杆i的前一个连杆i-1为固连坐标系，坐标系为Ωi-1(Oi-1Xi-1Yi-1Zi-1)，其中坐标系原点Oi-1为关节轴线Zi-1与公法线ai-1的交点，Xi-1与ai-1重合，Zi-1与关节轴线重合。坐标系Ωi可以通过坐标系Ωi-1绕Xi-1轴转角αi，沿X i-1轴平移Ai，绕Zi-1轴转角θi，然后沿Zi-1轴平移Di四步获得MDH参数，则变换矩阵如下：

　　i-1Ti=RX(αi)×DX(Ai)×RZ(θi)×DZ(Di)

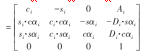
　　式中：ci为cosθi；si为sinθi；cαi为cosαi；sαi为sinαi。

　　从基座开始推导，得到末端基于基座坐标系的变换矩阵，表达式为：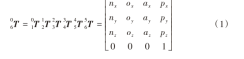

　　式中：nx、ny、nz，ox、oy、oz，ax、ay、az分别为机器人末端的单位主矢量x、y、z相对于基坐标系的x、y、z的方向余弦；px、py、pz分别为机器人末端的坐标原点相对于基坐标系的x、y、z的位置。

　　1.3运动学反解

　　机器人逆运动学是根据机器人的末端位姿信息、机器人连杆参数、变量的变化范围、机器人位型等信息，求解机器人的关节角。当六自由度机器人的几何结构满足Pieper准则时，机器人具有解析解求解机器人逆运动学模型，对于不满足Pieper准则的六自由度机器人，则只能使用数值解求解。文中的机器人满足Pieper准则，因此可使用解析解进行求解。

　　解析解对机器人进行逆运动学求解，可以适用于相同类型不同尺寸的机器人，只需要修改MDH连杆参数即可实现。同时，使用解析解进行求解，可以极大减少计算耗时，因为提前通过公式推导将大量费时的矩阵计算解决了，计算机只需要进行简单的四则运算，计算速度快，算法时间复杂度低。

　　使用解析解求解机器人逆动力学，就是根据式（1），通过连杆变换矩阵的矩阵运算，直接求解出关节变量θ1、θ2、θ3、θ4、θ5、θ6。将式（1）简化为式（2），并进行矩阵的变换，可以解得关节的值。

　　T=T T T T T T（2）

　　本文按照θ1、θ2、θ3、θ4、θ5、θ6的顺序求解关节角。

　　（1）求解θ1

　　将式（2）等号两边同时乘以[T]-1，得

　　T[T]-1=T T T T T（3）

　　式（3）等号两边的第3行第4列的元素相等，通过化简可以解得θ1的两个解。

　　θ1=a tan 2(ry,rx)-a tan 2((-d2-d3),±)（4）

　　（2）求解θ2

　　令式（2）等号两边的第1行第4列元素和第2行第4列元素相等，通过化简计算，可以得到θ2的求解公式。

　　■|θ2=a tan 2(m,n)-a tan 2(c,±vm2+n2)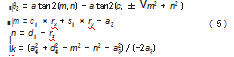

　　（3）求解θ3

　　将式（2）等式左右两边同时左乘[T]-1得

　　T T=T T T（6）

　　将式（6）中第1行第4列元素和第3行第4列元素相等，化简计算得到θ3的角度计算公式：

　　■θ23=a tan 2(d4,-a4)-a tan 2((rz-d 1-a3×s2),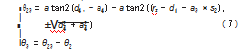

　　（4）求解θ4

　　根据式（6）中第1行第3列和第3行第3列对应相等，并简化计算：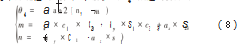

　　（5）求解θ5

　　根据式（6）中第2行第3列元素对应相等，并化简计算，可以计算出θ5的角度计算公式为：

　　θ5=a cos(az×c23-ax×c 1×s23-ay×s 1×s23)（9）

　　（6）求解θ6

　　对式（2）等号两边同时乘以[T]-1，得

　　对式（10）中第1行第1列的元素和第1行第3列的元素对应相等，并进行化简计算后可以得到θ6为：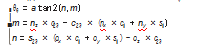

　　至此，已经得到θ1、θ2、θ3、θ4、θ5、θ6的全部可行解，因为θ1、θ2、θ3都存在两个解，因此总共可以解得8组解。

　　2工业机器人轨迹规划
       2.1机器人末端路径构造

　　以圆弧路径为例，指定路径起点Ps、中点Pm和终点Pe，采用矢量方式求圆心坐标Po。如图2所示，弦PsPm与弦PmPe的中垂线交点为圆心Po。根据右手法则，弦PsPm与弦PmPe组成平面的单位法向量n=Ps P m×Pm Pe/Ⅱs Pm×Pm PⅡ。令PsPm和PmPe的单位向量分别为nsm和nme，根据右手法则计算得PsPm和PmPe的中垂线单位向量为n 1=n×nsm和n2=n×nme。令s 1和s2分别表示PsPm和PmPe的中点，e 1=s 1+n 1，e2=s2+n2。过e2点作中垂线s1e1的平行线，过点s2作中垂线s1e1的垂线，并分别与中垂线s1e1及其平行线相交于点a1和a2。根据相似三角形可求得圆心坐标位置为：

　　Po=Ⅱs2 a 1Ⅱ/Ⅱs2 a2Ⅱ⋅s2 e2+s2（3）

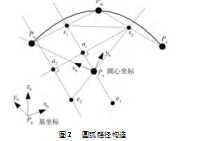
　　令Po Ps和Po Pe的单位向量分别为nos和noe，则圆弧角可以通过式（4）计算。

　　α=arccos(nos⋅noe)（4）

　　以圆心指向起点的直线Po Ps的方向作为圆弧坐标的x轴，法线向量n作为z轴，则所构造圆弧的坐标系可表示为：

　　2.2机器人末端速度规划

　　将圆弧等长分为20份，作为粗插补点，构建累加递增的长度数组L=[L 1,L2,⋯,L20]，其中第i个元素Li=oj=Li+Loi，数组中第1个元素L 1=Lo1，其中Loi(1≤i≤20)为第i段路径的长度。

　　如图3所示反向前瞻规划的原理，从第k段开始，末速度为0，以加速度A max反向加速，能达到的最高速度为速度Vmax k。以Ve=min(Vlim,Vmax k)作为第k-1段的末速度，如果Ve≥Vlim，则第k-1段不需要处理，直接可令Vmax k=Vlim，否则继续以加速A max反向加速，然后再取Ve=min(Vlim,Vmax k-1)。一直到第二段路径才结束，从而得到第一段路径的最大允许末速度为Ve=min(Vlim,Vmax 2)。其中，Vlim为用户给定的速度限制，第i段的最大可达速度的计算方法为Vmax i=2Amax Loi+Ve2。

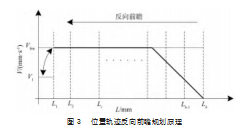
　　完成反向前瞻后，进而可对第一段进行正向规划。根据最大加速度A max和最大速度限制Vlim，令首速度为Vs，末速度为Ve，首先计算能够到达的最大临界速度Vc：

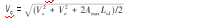
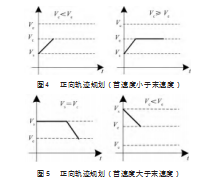
　　根据最大临界速度Vc与最大速度限制Vlim的关系，得到具体速度规划情况如图4~5所示。当Vs<Ve时，具体规划情况如图4所示；当Vs≥Ve时，具体规划情况如图5所示。

　　3软边界实时监控

　　反向前瞻同时采用滑动窗口的思想，目的是保证机器人能在窗口内的轨迹终点平稳减速到0。滑动窗口的原理：假设设定一个窗口为5的窗口，并且现在存在20段路径，则将从第6段轨迹开始，进行反向前瞻，得到第1段的末速度，再根据正向规划得到第1段内的速度曲线；之后窗口向后滑动一段，同时窗口大小保持不变，即从第7段开始反向前瞻，并正向规划第2段内的速度曲线；直到无法继续滑动，即从第20段开始反向前瞻，并正向规划第15段内的速度曲线，此时则开始减小窗口大小，每次减1，直到20段的速度曲线全部规划完毕。滑动窗口思想如图6所示。

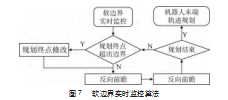
　　添加软边界实时监控后，在窗口进行滑动前，先进行一次边界检测，当检测到在本次规划时将超出边界，则将规划终点从线段终点修改为超出边界前的最后一次规划点。同时继续进行反向前瞻正向规划，在最后一次规划点处停下。算法流程如图7所示。

　　4数值仿真及分析

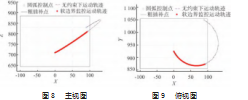
　　根据前文所示的机器人模型和运动学公式，得到机器人末端在初始位置下的位置信息为[0，955，745]。设定机器人末端的工作空间为以[-100，855，645]为顶点，长宽高各200 mm的正方体工作空间。以[0，925，700]为圆弧起点，[95，875，785]为圆弧中点，[90，1050，800]为圆弧终点，根据第2.1节中提到的空间圆弧路径构造方法，得到圆弧轨迹在工作空间中的主视图、俯视图分别如图8~9所示。由图可知，圆弧轨迹的3个控制点均在工作空间内，进行圆弧规划后的轨迹如图中的实线所示。但是规划得到的圆弧轨迹存在部分超出工作的部分，根据软边界进行判断，可以得到超出软边界前的轨迹如中粗点线所示。

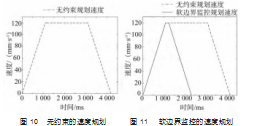
　　根据第2.2节所提到的机器人末端速度规划，得到如图10所示的速度规划图。再引入软边界实时监控，得到如图11所示的速度规划图。可以清楚地看到，图11中的匀速段缩减，并提早进行减速，最终能够在轨迹超出软边界前进行停止。

　　5结束语

　　本文首先说明了机器人的模型建立方法的差异，并选择MDH方法建立机器人模型；然后推导机器人正逆运动学算法，并采用反向前瞻正向规划的方法对机器人末端进行速度规划，再引入软边界限制，研究基于软边界实时监控的工业机器人轨迹规划算法，实时监测轨迹规划中规划点是否超出软边界。当检测到规划点将超出软边界时，可以及时调整规划路径，并立即调整速度使机器人能够在边界前停止，使末端不超出边界。对于机器人笛卡尔空间的轨迹规划具有重要意义。

　    参考文献：

　　[1]郭梅静,李江,刘晓晓.基于视觉定位的机器人关节装配应用研究[J].信息记录材料,2023,24(7):175-177.

　　[2]李家鹏,王剑,李学伟,等.工业机器人装箱与码垛工作站数字孪生系统设计与优化[J].现代制造工程,2023(10):44-49.

　　[3]文国军,祁靖烨,赵权,等.基于数字孪生的工业机器人虚实联动系统开发[J].机床与液压,2023,51(15):9-14.

　　[4]郑永杰,刘旭东,周桐,等.机器人与自动化技术在工艺智能化升级中的优化策略研究[J].制造业自动化,2023,45(10):216-220.

　　[5]蔡国庆,郝瑞林,周利杰,等.食品搬运机器人工作空间仿真与轨迹规划[J].食品与机械,2022,38(9):114-119.

　　[6]何成刚,朱润智,黄挺博,等.工业机器人轨迹规划与优化研究进展[J].现代制造工程,2023(7):150-159.

　　[7]田勇,张露,林开司.六自由度工业机器人轨迹规划与仿真[J].玉溪师范学院学报,2020,36(6):49-56.

　　[8]董威,倪受东,张琛.焊接机器人笛卡尔空间轨迹规划研究[J].机械制造,2019,57(4):20-23.

　　[9]卓扬娃,白晓灿,陈永明.机器人的三种规则曲线插补算法[J].装备制造技术,2009(11):27-29.

　　[10]梁艳阳,王利,姚超智,等.基于Hermite方法的机器人任务空间二阶平滑位姿路径构造[J].机床与液压,2022,50(21):20-25.

　　[11]杨广新.基于MATLAB的6R机器人轨迹规划速度分析[J].机电工程技术,2020,49(10):144-145.

　　[12]梁兆东,肖永强,游玮,等.工业机器人误差补偿运动学算法设计[J].机械设计与制造,2021(5):273-275.

　　[13]CRAIG J.Introduction to robotics mechanics and control[M].New Jersey:Pearson Education Intenationa1,2005.

　　[14]冯瑶,公茂震.6R机器人笛卡尔空间轨迹规划中的逆运动学[J].自动化技术与应用,2018,37(6):68-73.