摘要：蜂窝板具有强度高、质量轻、抗振性强等显著优点，广泛应用于航空航天、汽车、造船等技术密集型产业。随着工艺技术的进步，蜂窝板逐步在工业自动化领域得到应用。提出了一种蜂窝板有限元等效建模方法。确定结构的单胞，结合经典层合板理论，应用狄利克雷边界条件，确定结构的方向向量，以有限元仿真为工具，拆分出3个子分析步，计算出蜂窝板的等效均匀各项同性模型。比较等效模型与完整模型仿真结果，静态变形量的相对误差仅有2%，前3阶模态的相对误差均不到1.8%。随后基于这种建模方法，采用实验设计，针对特定的应用场景，设计响应曲面实验，确定了关键因子和显著交互效应，并给出最优组合。提出的方法大幅度降低蜂窝板结构的网格数量，提高求解效率，可广泛应用于各种周期性结构的有限元建模。

　　关键词：蜂窝板；有限元；建模；实验设计

　　0引言

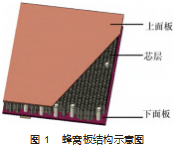
　　蜂窝板源自仿生学，其结构质量小、强度高，受到冲击载荷时胞壁结构发生弹塑性变形，同时吸收冲击能量，具有极其优异的力学性能，因而广泛应用于航空航天、轨道交通领域，并逐步在工业自动化领域得到更多的应用[1-4]。由于蜂窝板的结构较为复杂，涉及到壁长、壁厚、壁高等不同参数组合，设计阶段必须严格校核蜂窝板的强度。蜂窝板一般由上下面板和中间的芯层组成，面板与芯层之间采用黏结剂连接[5]，如图1所示。工业领域的蜂窝板，其面板与芯层的材料通常为铝合金。

　　等效刚度是蜂窝板研究中的热点。研究蜂窝板的等效刚度主要可分为两种方法，即解析法和数值法。解析法的显著特点是公式清晰直观，但推导中往往需要引入一定假设，造成一定的精度损失，计算较为复杂，因而适用范围受限，不太适合工程化应用[6]。解析法相关研究较多，一般采用经典层合板理论对蜂窝板进行简化计算。数值法包括渐进均匀化方法、代表体元法、变分渐进法和直接平均法等，其中前两种为常用方法。渐进均匀化方法具备严格的数学基础，需要求解定义于单胞上的偏微分方程组。这种方法的数值实现难度较大。而代表体元法(RVE)是从周期性结构中取出单胞作为研究对象。通过对单胞施加单位位移或力边界条件，求解应变能并建立等效的均匀材料实体[4,7]。这种方法虽然不是基于严格的数学理论，但胜在力学概念清晰，易于操作，因而大量应用于周期性结构材料弹性性质的预测当中。

　　随着计算机科学的迅速发展，有限元法也越来越多地参与到蜂窝板研究当中。有限元法主要分为全实体建模法和等效板建模法。前者需要将蜂窝结构按实体进行建模。一旦面对较为复杂的机械结构，往往需要耗费巨大的计算资源和时间，甚至造成求解过程出错而无法仿真。因而难以推广全实体建模法。等效建模法则更为实用，其特点是采用解析法或数值法求解，将蜂窝板等效为一块连续的各项同性的板件[8-10]。得益于计算机运算能力的飞速发展，等效建模法与有限元技术相结合，在蜂窝结构的材料性能计算与预测领域相得益彰。本文采用RVE法进行蜂窝板结构的有限元等效建模，无需复杂的公式推导，仅基于商业有限元仿真软件进行插件开发，实现周期性结构的快速等效建模。进而采用实验设计，针对特定的应用场景，用等效结构实现多组蜂窝板的变形仿真，确定最优组合，科学而高效地完成蜂窝结构的选型设计工作。

　　1蜂窝板的等效建模

　　蜂窝板芯层的单胞如图2所示，主要参数包括壁长、壁高、壁厚等参数。需要注意的是，单胞是组成周期性结构的最小单位。整体结构可看作由单胞沿着阵列方向复制组成。因此，该单胞包含一个正六边形壁面、两个横向的半壁。壁面结构与相邻的单胞共享六条边，因此单胞的六条边厚度取实际壁厚的一半，而两个半壁的壁厚为真实蜂窝的壁厚。

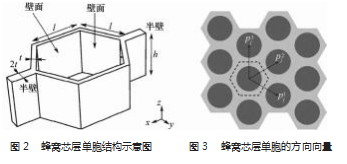
　　常见的蜂窝板芯层有3个方向向量，分别对应正六边形的3组对边，如图3所示。从图中可以发现，任选一个单胞，将其沿着3个方向向量的方向阵列，即可得到整块的蜂窝芯层结构。为了验证等效结构的可行性，需要完整的有限元模型作为对照。完整蜂窝板的有限元模型如图4所示。采用实际尺寸1∶1建模，层板和芯层采用绑定连接。该蜂窝板的上面板需要承载一个较大的载荷，下面板固定在支撑结构上。蜂窝板内部均匀布置了牙套，安装于牙套中的螺钉将蜂窝板与支撑结构固连起来。蜂窝板下面板上另外均匀布置了气浮脚，为蜂窝板的远端提供支撑，减小由于重力和外载荷而产生的变形。对单胞施加单位位移边界条件，令其应变能和一个均匀材料的应变能等效，从而求出等效性质[4]。采用二次开发的周期性结构等效插件，进行等效均匀材料的求解。输入条件是单胞的结构尺寸参数和材料属性。原始材料与求解得到的等效材料的属性对比如表1所示，完整模型的材料为6061铝合金。

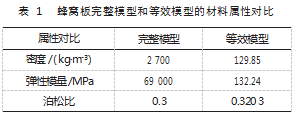
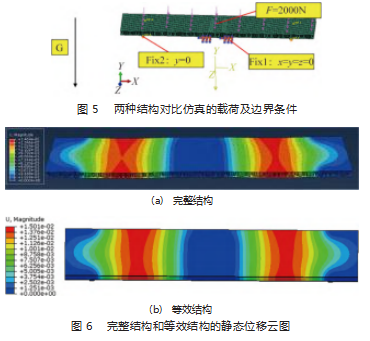
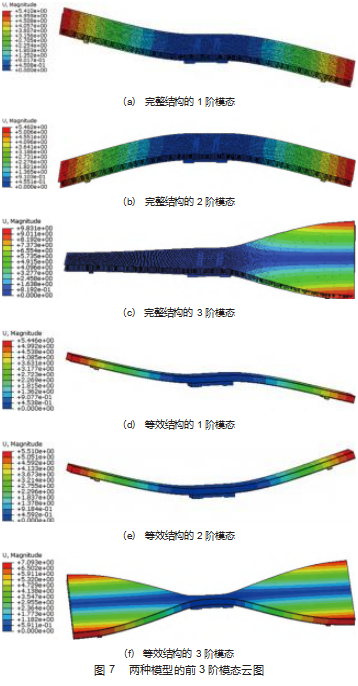
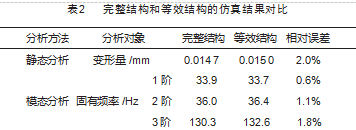
　　随后，分别对完整模型和等效模型施加载荷，蜂窝板上面板施加2 000 N的面载荷，下面板安装螺钉的位置设置Fix约束，气浮脚支撑位置设置竖直方向Fix约束，如图5所示。分别选用通用静态分析步和模态分析步进行仿真。两种模型的静态位移云图如图6所示。两种模型的前3阶模态云图如图7所示，详细数据对比如表2所示。从完整结构的静态分析结果来看，蜂窝板的最大变形出现在缺乏Fix支撑的部位。且由于结构对称，总体的变形呈对称分布。等效结构的变形分布也呈现出同样的特点。仅有的区别是，等效结构为均匀材料，变形的连续性更好，缺乏一些细微特征的变形信息。但总体来看，分布趋势与完整结构保持一致，主要区域的变形量与完整结构极为接近，最大静态变形的相对误差仅为2%。两种结构的前3阶模态振型相似，位移的分布较为一致，而前3阶固有频率的相对误差小于1.8%。从工程应用的角度而言，采用等效结构即可满足大多数场合的精度要求，但带来的好处是极大降低网格数量，大幅度提高计算效率，降低计算报错的概率，尤其适用于含蜂窝结构的复杂机械结构的仿真。

　　2基于蜂窝板等效模型的实验设计

　　实验设计(Design of Experiment)简写为DOE，其根本方法是正交设计，是研究与处理多因子实验的一种科学方法[11]。DOE的核心目标是合理安排实验方案，减少实验次数的同时，确保因子分布均匀、分散，保证计算精度。DOE广泛应用于因子的筛选、因子水平搭配及实验优化等[12-13]。常用的DOE方法包括部分因子DOE、全因子DOE和响应曲面DOE。部分因子和全因子DOE不考虑因子的交互效应，适合用来做关键因子的筛选，尤其是部分因子DOE。而响应曲面DOE可评估交互效应的影响，且含有平方项。但响应曲面需要的实验组合很多，实验成本很高。实际操作中的一般做法是用部分因子DOE去除不显著因子，剩下少量关键因子，再采用全因子DOE或响应曲面DOE进行第二轮实验，以得到更准确的实验结果。采用有限元与DOE相结合的方式，将实物实验替换为仿真模拟，降低实验成本，并大幅度提升多因子结构的设计能力和效率[14]。

　　上文成功将复杂的蜂窝结构简化为各项同性的等效材料并验证了等效结构的可靠性。因此，变更蜂窝材料的参数后，迅速重新计算其等效结构，并以等效结构施加边界条件和载荷，并快速求解。正是由于等效结构的出现，使得含蜂窝板的复杂结构的仿真DOE成为可能。经过充分调研和鱼骨图分析，确定3个因子作为DOE的输入[15]。由于因子数不多，故跳过部分因子和全因子实验设计，直接采用响应曲面设计，因子水平如表3所示。因子水平的设置均考虑到实际工况，易于安装维护，兼顾强度和质量。

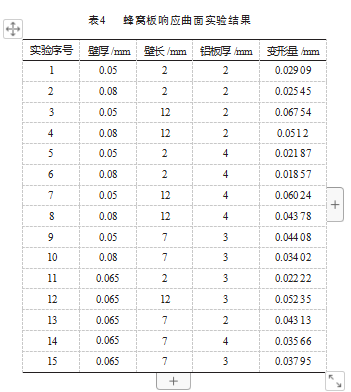
　　采用专用软件生成响应曲面DOE的实验方案。每一个因子组合均需要比照图2建立单胞，以RVE法计算蜂窝芯层的等效结构。随后以等效结构代替蜂窝芯层，建立工况有限元模型。施加载荷和边界条件后进行求解，并输出目标位置的变形量。响应曲面实验结果如表4所示

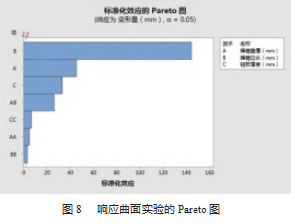
　　采用专业软件对实验结果进行显著性分析，得到的Pareto图如图8所示。Pareto图以t检验为基础，将各效应的t值作为纵坐标，并根据显著性水平计算临界t值。绝对值大于临界值的因子确定为显著因子。该因子分析中，显著性水平取0.05，采用后退法进行因子筛选。显然3个因子对变形量的影响显著，每个因子的平方项影响也显著，且壁厚和壁长的交互效应对变形量的影响显著。根据因子分析的结果，剔除不显著因子，并计算显著因子的回归方程为：

　　s=0.059 86−0.642A+0.006 355B−0.012 05C+

　　壁厚0.077 3 mm，壁长2 mm，铝板厚4 mm时，蜂窝板取得最小变形量0.018 5 mm。根据回归方程，也可进行因子高低水平范围内任意因子组合的结果预测，将三因子的数值代入回归方程即可计算出变形量。

　　3结束语

　　典层合板理论为基础，应用狄利克雷边界条件，确定单胞方向向量，以有限元仿真为工具，拆分分析步，计算出蜂窝板的等效均匀各项同性模型。比较等效模型与完整模型仿真结果，静态变形量的相对误差仅有2%，前3阶模态的相对误差均不到1.8%。基于该建模方法，DOE和有限元仿真相结合，确定特定应用功能场景下蜂窝板结构的最优组合。该方法大幅度降低蜂窝板结构有限元模型的网格数量，大大提高求解效率，可广泛应用于各种周期性结构的有限元建模，尤其是含有复杂周期性结构的机械系统建模。

　　参考文献：

　　[1]蔡园武,徐亮,程耿东.正六角形单胞周期性蜂窝板等效刚度研究[J].大连理工大学学报,2014,54(4):377-383.

　　[2]潘凤丽,李光.基于Ansys Workbench的塑料蜂窝板仿真分析及优化[J].包装工程,2016,37(23):44-49.

　　[3]张晓翠,王林龙.基于ANSYS的铝合金蜂窝板的力学性能仿真[J].机械设计与制造工程,2017,46(12):34-36.

　　[4]蔡园武.周期性板结构的渐近均匀化方法及微结构优化[D].大连:大连理工大学,2014.

　　[5]徐洋,王皓辉,盛晓伟.基于Hyperworks的六边形蜂窝板铺层等效建模方法研究[J].振动与冲击,2018,37(23):45-51.

　　[6]王巍.蜂窝板结构等效建模方法及其在太阳翼帆板上的应用研究[D].沈阳:东北大学,2018.

　　[7]L Gigliotti,S T Pinho.Exploiting symmetries in solid-to-shell ho⁃mogenization,with application to periodic pin-reinforced sand⁃wich structures[J].Composite Structures,2015(132):995-1005.

　　[8]孙卫青,程伟.基于响应面全局优化技术的蜂窝板材料性能参数修正[J].材料工程,2019,47(5):159-166.

　　[9]王钢,赵才其,顾业,等.铝合金蜂窝板-杆组合网络结构的等效刚度研究[J].建筑结构,2022,52(12).

　　[10]赵辽翔,吕文俊,王君香,等.ABAQUS铝蜂窝板GUI建模程序开发研究[J].中国高新科技,2022(2):16-19.

　　[11]成晨.基于CAE与DOE的家用电钻优化设计[D].苏州:苏州大学,2016.

　　[12]陈秀明,陈大伟,秦鹏,等.基于DOE和CAE的灰铸铁件残余应力影响因素研究[J].现代铸铁,2021(5):19-22.

　　[13]康一坡,曹正林,李俊楼,等.DOE技术在螺栓连接有限元分析中的应用[J].机械设计,2021,38(11):85-89.

　　[14]郭伟科,吴智恒,张华伟,等.基于DOE的电主轴温度场分析[J].机电工程技术,2015,44(8):133-136.

　　[15]胡清珍.影响微波炉用电镀烧烤架镍迁移超标的原因调查分析[J].机电工程技术,2017,46(9):124-127.