摘要：为提高高速列车主动悬挂控制系统的精度，提出了一种基于差分进化（DE）改进的灰狼算法（GWO）的高速列车主动悬挂模糊双反馈主动控制策略。该策略基于高速列车主动悬挂系统垂向六自由度模型，采用了具有双反馈机制的模糊PID控制器，并用DE-GWO算法调整PID参数，该算法通过采用差分进化机制防止算法过早收敛。将采用改进灰狼算法优化后的模糊双反馈PID控制器与被动悬挂系统、PID控制器和优化前的模糊PID控制器进行比较，结果显示该控制策略使主动悬挂的加速度均方根值优化了45.80%，垂向平稳性指标降低至1.515，平稳性提高了25.07%。所提主动控制策略应用在高速列车主动悬挂系统时的垂向振动控制效果显著，可有效改善高速列车运行均衡性。

　　关键词：主动悬挂系统；模糊控制；灰狼算法；差分进化算法；双反馈

　　0引言

　　悬挂系统的稳定性影响高速列车运行的平稳性。相比于常规的被动悬挂系统，高速列车主动悬挂系统能够针对当前的行驶条件自主调整，能有效解决高速列车垂向振动抑制问题，是当前国内外学者研究的重点之一[1]。Zhou等[2]经过了长期的研究与探索后，将神经网络控制算法运用于高速列车主动悬挂系统的控制；段红杰等[3]将非线性随机振动理论铁道应用于客车半主动随机隔振系统中；张亚彤等[4]结合模糊控制和PID控制理论，并将其用在列车主动悬挂系统中，控制效果较为显著。

　　研究者们针对灰狼优化算法（Gray Wolf Optimiza⁃tion，GWO）提出一系列改进方法，进一步提高算法寻参能力、收敛速率、保证种群多样化。Islam等[5]为提高算法全局寻参的多样性，将遗传算子引入GWO算法，使种群进行变异；徐松金等[6]在GWO算法的基础上，引入动态收敛算子，防止算法早熟收敛；魏政磊等[7]采用了控制参数非线性的调整策略来提高算法全局搜索的多样性；罗佳等[8]引入了混沌序列，该方法有效解决了算法出现局部最优的情况；朱海波等[9]将优胜劣汰策略应用于GWO算法，提升种群多样化，进一步提高了算法的寻参准确性。

　　通过应用多种算法可以有效地改善高速列车的主动悬挂垂向振动，从而大大增强了列车的营运平稳性[10-12]。因此，本文基于高速列车主动悬挂系统模型，结合差分进化（Differential Evolution，DE）算法、GWO算法、模糊PID控制器等多种算法，进一步改进了算法的收敛速度、全局搜索精度，并且引入了超双反馈机制，提出了一种基于改进GWO算法的高速列车主动悬挂模糊双反馈主动控制策略，实现了更好的控制效果。通过将模糊理论、超双反馈机制、GWO算法与传统的PID控制器相结合，可以大幅度地增强控制器的稳定性，并通过仿真实验来评估其在降低振动方面的有效性。

　　1高速列车主动悬挂系统模型
　　1.1数学模型

　　本文主要构建了高速列车半车垂向六自由度悬挂系统动力学模型，不计铁轨的弹性变化以及轮对与铁轨无空气缝隙，忽略车体、构架、轮对弹性变化[13]。高速列车主动悬挂系统结构如图1所示。

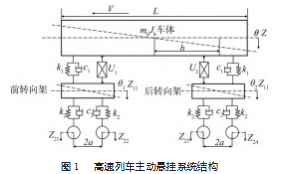
　　车体动力学分析方程可表示为：

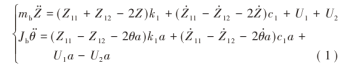
　　前转向架动力学分析方程可表示为：

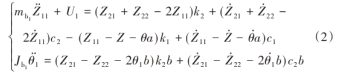
　　后转向架动力学分析方程可表示为：

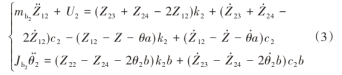
　　式中：Zb、Z.b、Z…b分别为高速列车车体垂向位移、速度、加速度；Z 11、Z 11、Z 11、Z 12、Z 12、Z 12分别为高速列车前后转向架的垂向位移、速度、加速度；U1、U2分别为前后二系悬挂系统作动器提供的作动力；Z2i、Z.2i为第i（i=1，2，3，4）轮对的垂向位移与速度。

　　1.2轨道不平顺激励

　　轨道不平顺激励是指轨道上的不规则振动或摇晃，通常由轨道本身或列车运行时的外部因素引起。这些不平顺可能会导致列车的震动和噪音增加，对列车和轨道的磨损和损坏也会加剧。因此，轨道不平顺激励是铁路运行安全和可靠性的重要考虑因素。高速列车由于受到铁轨不平顺激励，其垂向动力学性能受到较大影响，引起车体-铁轨耦合系统产生不规律振动响应。高速列车悬挂系统的外部激励选取德国铁轨垂直不平顺谱，分析式如式（4）所示。

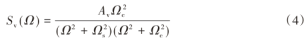
　　假定高速列车的营运速度为v，通过式（4）计算得到铁轨垂直不平顺的时域谱为：

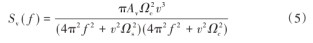
　　德国铁轨垂直不平顺谱的参数值如表1所示。设速度为300 km/h、fmin为0.5 Hz、fmax为200 Hz、T为30 s，仿真得到的铁轨垂向不平顺，如图2所示。

　　2基于改进GWO的模糊双反馈控制策略

　　2.1模糊控制

　　模糊控制的基本思想是将输入和输出的变量都映射为模糊集，然后将控制规则表示为模糊关系，控制量最终借由模糊推理得到。模糊推理是一种基于模糊规则的推理方法，可以将模糊输入转化为模糊输出，是模糊控制的核心。模糊控制具备了无需构建受控对象的数学模型、易于控制非线性系统、设计简易、鲁棒性强等优点[14]。

　　2.2模糊PID控制

　　传统PID控制表达式为：

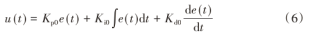
　　式中：u(t)为输出；e(t)为预期结果与最终结果之间的偏差；Kp0、Ki0、Kd0均为PID控制器的初始参数，同时也是模糊控制的输入，其变化会影响高速列车的营运状态。

　　因此，需要对PID参数实时调整，就可以使车体合成振动加速度尽可能地趋于0。其控制过程为：首先将车体垂向加速度及加速度的变化信息输入到模糊控制器中，然后调整参数ΔKp，ΔKi，ΔKd，并作为模糊控制器的输出。在此基础上还需要综合考虑初始值和校准值，对PID控制器的输入进行优化，最终获得最优的线性控制力U来控制整个悬挂系统。终参数可以通过以下公式计算得到。

　　式中：Kp，Ki，Kd为模糊控制调节后的系数，Kp0，Ki0，Kd0为模糊控制的变量。

　　本文构建一个基于高速列车主动悬挂系统的模糊PID控制器仿真模型，其中，通过计算高速列车营运过程中在垂直方向上的加速度，并将其与点头方向的加速度进行比较，以确定车辆的最佳营运状态。

　　2.3基于差分进化改进的灰狼算法

　　通过引入差分进化思想，GWO算法可以有效地改善狼群的觅食能力[15]，可以有效地防止GWO算法过早收敛，提升全局寻参能力。该进化机制可以得到适应能力更强的生物种群，从而实现更高效的觅食与生存[16]。

　　狼群在进化过程中，会根据环境的变化，经过淘汰得到觅食能力更出众的个体作为父代，以提高种群的生存能力与适应力。对β狼和δ狼进行反复实验来确定其差分矢量，变异因子则是由动态缩放因子与α狼共同来确定的，其可以由以下表达式计算得到。

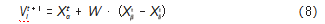
　　式中：W为是一个可以随时间变化的缩放变量，其取值方式如式（9）所示。

　　式中：t为迭代次数；fmin、fmax为缩放变量的2个重要指标。

　　当缩放变量W变高时，GWO算法的前期的全局寻找性能会得到提升；而当缩放变量变低时，t的变化会导致算法的后期的局部寻找性能受到影响。

　　在狼群中，核心个体Xti与差分矢量Vt+1通过交叉操作产生边缘个体Yt+1。当边缘个体Yt中有一个基因由差分矢量Vt提供时，核心个体Xt一定发生变异。通过比较交叉概率变量S与产生的随机混沌数，来判断变异基因是由谁提供的，其交叉操作为：

　　式中：利用随机变量rand（i）保证狼群个体至少有一组变量来自变量Vit[17]；S为交叉概率变量，交叉概率S选取的恰当与否，决定了收敛速度的快慢和局部搜索能力的高低；随机变量rand（j）为服从均匀分布的随机混沌数。狼群经过变异和交叉操作产生边缘个体Yit+1，与核心个体Xit比较，筛选出二者中适应度值更优的作为狼群的新一代，如式（11）所示。

　　在狼群中，fclose为个体之间的距离极差值，可以表示为：

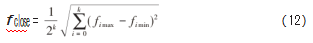
　　式中：fimax为第i个个体间的最大距离、fimin分别为第i个个体间最小距离，k为目标函数数量，选择Xti和Vt+1中适应度值最高的作为新一代个体。算法步骤为：

　　（1）种群初始化，通过随机算法，生成狼群的初始位置。初始化系数向量为A、C和a；

　　（2）计算得到狼群适应度系数，选取系数最小的3只狼，记为α、β和δ狼；

　　（3）更新狼群位置。根据式（8）～（12）得到γ狼的位置；

　　（4）差分进化操作。选择种群父代个体，通过重组和变异，得到新的子代并选出新的α、β和δ狼；

　　（5）根据上一步操作更新参数A、C和a；

　　（6）判断算法是否满足终止要求，如果满足终止要求，结束算法并将α狼作为期望最优解输出；若未满足，则继续执行步骤2。

　　2.4超双反馈机制

　　超双反馈算法的灵感来源于人体的神经内分泌调节机制，这种机制具有多路负反馈，即人体器官分泌的激素不仅作用于下个内分泌器官，同时还作用于本身，这就是超双反馈的思想[18]。非线性反馈函数如下：

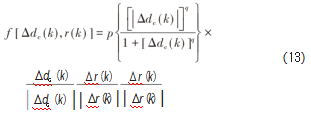
　　式中，p，q为算法系数；Δd（k）为误差增量；Δr（k）为输出增量。u（k）为模糊PID控制器的输入，有：

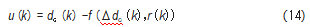
　　2.5基于DEGWO的模糊双反馈控制

　　研究表明，传统PID参数的设定存在着明显的主观性，从而限制了其控制精度。采用差分进化改进的灰狼算法整定PID控制器参数，寻找到目标最佳值，使高速列车悬挂系统能够在平稳的状态下运作[19]。如图3所示，使用差分进化改进的灰狼算法优化初始参数，然后再将其输入到模糊PID控制器中，同时加入超双反馈机制提升控制的准确性，使设计的高速列车悬挂系统能更加稳定的运行[20]。

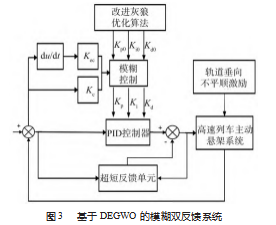
　　高速列车的安全性取决于其运行的平稳性，车身垂直加速度、点头角加速度以及二系悬挂系统动挠度是评价高速列车营运平稳性的重要依据，也是目标函数的3个重要指标。高速列车前、后悬挂系统目标函数为式（15），约束为式（16）。

　　式中：Q 1(x)，Q2(x)分别为前、后悬挂系统目标函数；Zb，Zbp分别为主动、被动悬挂系统车体垂向加速度；（Zb－Zt1－Ibθb）1，（Zb－Zt1－Ibθb），（Zb－Zt2+Ibθb）1，（Zb－Zt2+Ibθb）分别为高速列车主动、被动悬挂系统前后转向架二系悬挂系统的动挠性表达式；RMS为求均方根值；Xi为PID控制器参数所构成的矩阵。

　　通过采用差分进化算法改进的灰狼算法可以有效提升PID控制器的性能，其流程图如图4所示。利用改进的算法来调整PID控制器的3个关键参数，优化后的参数Kp0设为[0，19 000]，Ki0设为[0，175]，Kd0设为[0，6]。初始参数设定如下：狼算法的群体规模初始化为200，速度更新系数初始化为3，终值为0.6，最大迭代次数为200，惯性权重初始值为0.8，以提高算法的精准性。

　　在模糊PID控制器中，重要参数Kc，Kec，Kp0，Ki0和Kd0的值分别被设在以下范围：[-0.515，0.515]、[-23.50，18.50]、[0，19 000]，[0，175]，[0，6]。根据专家知识和列车振动情况，模糊控制规则参考文献[21]。

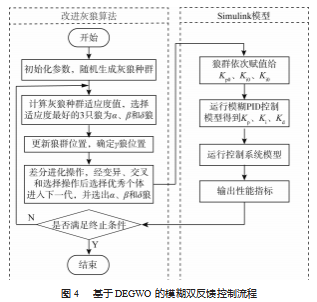
　　3实验仿真分析

　　3.1参数设置

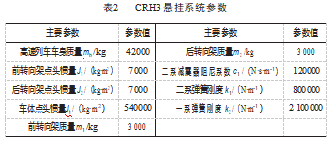
　　CRH3型号列车的悬挂系统参数[22]如表2所示。为了更好地控制高速列车的悬挂系统，首先搭建主动悬挂系统状态空间模型；然后分别设计被动悬挂系统控制器、传统PID控制器、模糊PID控制器和基于改进GWO算法优化后的模糊双反馈PID控制器；最后将设计的控制器模型分别应用到悬挂系统模型。

　　3.2仿真实验

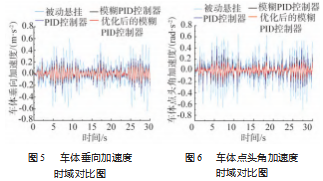
　　通过仿真得到高速列车悬挂系统车体垂向振动加速度对比图、车体点头角加速度对比曲线，如图5~6所示。可以看出，主动悬挂系统相较于被动悬挂系统，具有更好的垂向控制效果，而在3种PID控制器中，基于改进灰狼算法的模糊PID控制器的控制效果最好。

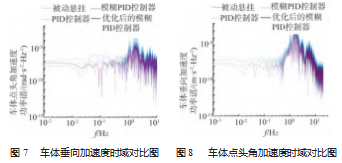
　　利用周期图法对得到的时域信号进行傅里叶变换，可以得到车体垂向加速度和点头角加速度的功率谱频域曲线，如图7~8所示。可以看出，基于改进GWO算法的模糊PID控制器功率谱密度最低。可初步断定于改进灰狼算法的模糊双反馈PID控制策略对高速列车主动悬挂垂向振动具有显著的抑制作用。

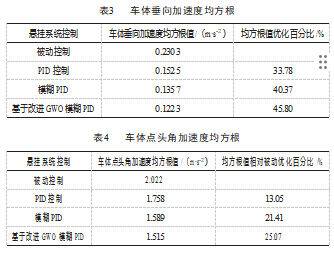
　　通过对表3~4的数据分析发现，使用改进的灰狼算法的模糊PID控制器性能较好。与被动悬挂系统相比，采用本文提出的控制策略使主动悬挂的加速度均方根值优化了45.80%，垂向平稳性指标也从2.022降低到了1.515，平稳性提高了25.07%。经过改进的灰狼算法的模糊PID控制策略在数据分析中显示出了优越的特性。

　　4结束语

　　本文旨在研究如何有效地控制高速列车的垂向振动，因此建立了一个非线性高速列车主动悬挂系统的动力学模型，并利用PID控制原理和模糊理论，对其进行了详细的研究，以期望达到更好的控制效果。还对比了被动悬挂系统、优化前的模糊PID控制以及基于改进灰狼算法优化后的模糊PID控制，以期望找到地控制高速列车的垂直振动的最优控制策略。通过仿真发现，采用改进的灰狼算法优化的模糊PID控制策略，不仅能够有效地提升高速列车的控制精度，而且控制性能也远远超过传统控制，同时也证明了在处理复杂的多输入多输出系统时，采用智能算法改进的模糊控制策略的优势是显而易见的。

　　参考文献：

　　[1]LI Danyong,SONG Yongduan,CAI Wenchuan.Neuro-adaptive fault-tolerant approach for active suspension control of high-speed trains[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(5):2446-2456.

　　[2]ZHOU Ronghui,ARGYRIOS Z,ROGER G.Integrated tilt with active lateral secondary suspension control for high speed rail⁃way vehicles[J].Mechatronics,2011,21(6):1108-1122.

　　[3]段红杰,陶浩.列车垂向振动的半主动随机隔振研究[J].噪声与振动控制,2007(2):15-18,24.

　　[4]张亚彤,王终军,徐妍琰,等.基于模糊PID控制的列车主动悬挂系统振动控制研究[J].工业控制计算机,2020,33(1):25-27.

　　[5]ISLAM S M,DAS S,GHOSH S.An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B(Cybernetics),2012,42(2):482-500.

　　[6]徐松金,龙文.嵌入遗传算子的改进灰狼优化算法[J].兰州理工大学学报,2016,42(4):102-108.

　　[7]魏政磊,赵辉,李牧东,等.控制参数值非线性调整策略的灰狼优化算法[J].空军工程大学学报(自然科学版),2016,17(3):68-72.

　　[8]罗佳,唐斌.新型灰狼优化算法在函数优化中的应用[J].兰州理工大学学报,2016,42(3):96-101.

　　[9]朱海波,张勇.基于差分进化与优胜劣汰策略的灰狼优化算法[J].南京理工大学学报,2018,42(6):678-686.

　　[10]CHEN B S,CHENG Y M,LEE C H.A genetic approach to mixed H2/H∞optimal PID control[J].IEEE Control Systems,1995,15(5):51-60.

　　[11]孟建军,白欢,牟健,等.一种求解车辆垂向振动系统H2/H∞多目标控制的方法[J].系统仿真学报,2016,28(12):2973-2978.

　　[12]田璐璐,郑玉强,郭文武.高速列车座椅主动悬挂系统的多模态控制研究[J].内燃机与配件,2020(2):4-7.

　　[13]孟建军,王终军,胥如迅,等.基于模糊复合策略的高速列车主动悬挂控制研究[J].系统仿真学报,2021,33(7):1554-1564.

　　[14]NGUYEN D P,NGUYEN N H,ALI A.A new fuzzy PID control system based on fuzzy PID controller and fuzzy control process[J].International Journal of Fuzzy Systems,2020,22(7):1-25.

　　[15]SUN Gaoji,YANG Bai,YANG Zuqiao,et al.An adaptive differ⁃ential evolution with combined strategy for global numerical op⁃timization[J].Soft Computing,2020,24(3):1-20.

　　[16]张新明,涂强,康强,等.灰狼优化与差分进化的混合算法及函数优化[J].计算机科学,2017,44(9):93-98,124.

　　[17]刘振泽,许洋,王峰明.改进差分进化算法在非线性模型预测控制中的应用[J].北京工业大学学报,2015,41(5):680-685.

　　[18]钟放鸿,张乐年,沈冬晖.基于模糊短反馈分数阶滑模的稳压器压力控制[J].计算机仿真,2022,39(3):273-277,324.

　　[19]彭冲,郑玲,李以农.基于粒子群优化算法主动悬挂系统作动器多目标优化设计[J].中南大学学报(自然科学版),2017,48(4):968-976.

　　[20]张蕾,廖绍雯.基于预测双反馈的3D打印机温度优化控制[J].计算机工程与设计,2021,42(7):2094-2101.

　　[21]张亚彤,王终军,徐妍琰,等.基于模糊PID控制的列车主动悬架振动控制研究[J].工业控制计算机,2020,33(1):25-27.

　　[22]吴神花,雷晓燕.交叉迭代算法求解车辆-轨道非线性耦合方程的收敛性讨论[J].华东交通大学学报,2015,32(3):23-31.