摘要：目前，双机械臂搬运系统的传统搬运策略存在搬运效果差、双机械臂同步性较差等问题，同时双机械臂的轨迹规划只针对末端轨迹，并未考虑运动状态下机械臂关节处产生的力矩。通过建立UR5机械臂的模型，分析双机械臂搬运状态的运动特点，建立了一种新的基于模糊滑模控制的双机械臂协同控制方法。首先通过对双机械臂建立运动学闭链约束关系，使得双机械臂能够实现期望轨迹运动，其次建立双机械臂的相邻误差交叉耦合同步策略，意在解决双机械臂之间的同步性问题，最后提出的模糊滑模控制策略，通过建立滑模面和滑模趋近律，实现机械臂的轨迹跟踪效果与关节处的控制输入稳定。最后通过对UR5机械臂进行滑模控制仿真，验证了该策略的可行性。

　　关键词：双机械臂搬运；模糊滑模控制；交叉耦合同步策略；运动学闭链约束；轨迹跟踪；UR5机械臂

　　0引言

　　随着双臂控制策略的不断发展，双臂也可应用于焊接或者机加工等传统工业场景内。双臂机器人因其能够执行更复杂的任务而备受关注[1]，在研究机器人控制策略时，首先需要建立机器人的运动学和动力学，然而双臂机器人的控制系统具有复杂的非线性特性和严重的耦合现象，难以建立准确的控制模型[2]。机械臂轨迹规划在机械臂控制技术中扮演着至关重要的角色，其轨迹质量直接影响机械臂的性能表现和使用寿命[3]。目前国内外学者对于双机械臂的轨迹跟踪控制研究也已经开展，其中Jyoti Ohri[4]等提出了一种独特的方法，将PID控制与鲁棒控制相融合，以解决轨迹跟踪问题中的挑战，特别是与摩檫力和不确定性相关的挑战。这一方法充分发挥了两种控制策略之间的协同作用。文献[5]针对目前双臂机器人传动阻抗控制不适合搬运柔性物体，提出了一种创新的双臂主从运动阻抗控制方法，成功地解决了传统主从控制在搬运柔性物体方面的限制。王会方等[6]研究了在面对不确定性的机器人系统中实现轨迹跟踪控制的问题，并提出了一种稳健的自适应PID控制算法。文献[7-9]在面对对象不确定性和外部干扰的情况下，提出了一种自适应鲁棒的跟踪方案，该方案利用神经网络自适应性补偿系统中的非线性部分。这种控制器可以确保系统的输出保持稳定，并且其算法设计简单，适用于在线控制。文献[10]在Seshagiri和Khalil的研究基础上，提出了一种改进的积分切换面设计，显著减少了系统的超调量。近年来，机械臂控制方法的研究焦点明显偏向于模糊控制、滑模控制，以及将自适应和神经网络等技术相互整合的领域[11]。文献[12]引入自适应神经网络控制到机械臂轨迹控制中，可以改善机械臂轨迹控制的性能。文献[13]提出基于滑模控制器的到达律设计方法，克服了传统的基于趋近律的SMC设计策略的不足。文献[14-15]提出了一种直接转矩控制方法，其核心策略基于滑模控制。文献[16]采用逆运动学方法降低了内外部扰动的边界。He W等[17]将自适应算法和神经网络算法结合应用于刚性机械手中实现准确的跟踪控制，文献[18]提出用单位向量函数代替最大-最小类型的控制。文献[19]应用自适应技术来实现机械臂的阻抗控制，取得了良好的控制效果。

　　以上研究的机械臂为2~3自由度机械臂，并且在双臂系统中滑模控制应用较少。为了进一步研究6自由度机械臂以及双机械臂系统的同步性和轨迹跟踪控制性能，根据现有的研究的优缺点，本文设计了一种基于滑模控制的双机械臂协同控制策略，以获得更好的控制精度和鲁棒性。

　　1双机械臂系统的模型建立
　　1.1闭链约束关系

　　本节主要讨论本文所使用的双机械臂协同控制面对被操作对象的运动轨迹规划。单机械臂的运动轨迹规划是基于被操作目标的估计通过坐标系的运动学转换而来的。因此建立的双臂协同系统坐标系如图1所示，在图1中{Wx,Wy,Wz}{Ox,Oy,Oz}分别表示为世界坐标系和目标物体坐标系；{ORX,OR Y,ORZ},{OLX,OLY,OLZ}分别表示为右侧机械臂基座坐标系和左侧机械臂基座坐标系；{R R R}{L L L}分别表示为右侧机械臂末端坐标系和左侧机械臂末端坐标系。

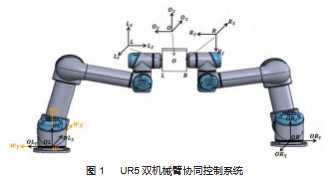
　　通过如图所示物体与机械臂之间的约束关系，之后可以求出机械臂的工具坐标系相对于机械臂的基座坐标系的旋转矩阵如式（1）所示。

　　式中：(T)-1为世界坐标系相对于机械臂的基坐标齐次转换；(T)-1为机械臂末端坐标系相对于物体质心处的齐次转换；T为已知的被操作物体的运动轨迹。

　　通过以上3项已知数据可以求出机械臂末端对于机械臂基座的动态轨迹，通过机器人的逆运动学式（2）求解可以求出每个关节在不同时刻的关节变化量。

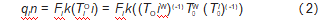
　　式中：i（R，L）为左或者右机械臂；n（1，2，…，6）为机械臂的关节；qin为机械臂关节处的角度；Fik为机器人的逆解方程。

　　1.2机械臂动力学方程

　　机器人动力学分析机器人的连杆之间的关节之间的关系，其中包含角度，角速度和角加速度等重要的参数信息。工业机器人和协作机器人中，由已知的关节驱动力求解机器人关节的运动参数为动力学正向求解，反之为动力学逆向求解。

　　动力学建模的方法有牛顿欧拉算法、拉格朗日方法、高斯求解法、凯恩求解法、施量对偶办法、罗伯逊魏登堡方程等。本文通过拉格朗日方法建立机器人的动力学模型。

　　拉格朗日动力学公式提供了一种推导动力学方程方法，从一个标量函数出发进行推导：

　　式中：M(q)为机器人的惯性质量矩阵；C(q,q.)为离心力和哥式力矩阵；G(q)为重力矩阵；d为扰动和未建模动力学的向量。

　　2模糊滑模控制的设计与证明

　　根据以上建立的动力学方程可知模型中有不确定性和外部干扰，为了解决以上不确定性和干扰而导致的多机械臂系统的跟踪同步问题，本章提出了采用模糊滑模控制方法，提高多机械臂的控制和跟踪效果。模糊控制（Fuzzy Control，FC）在许多应用中取代了传统技术。模糊逻辑的一个主要特征是它能够表达人类思维中的模糊性。传统的滑模控制所设计的滑模律因为存在有界性，因此机械臂关节的力矩会不断地震荡，多余多关节机械臂来说，震荡是致命的，本文为了消除关节的震荡，提出了一种模糊推理来达到相位，并且提出了模糊滑模控制，保证系统的鲁棒性。

　　首先构建滑模面s（t），以响应期望控制特性和性能[20]，这些轨迹被强制地位于滑动表面上，本文根据PID控制原理建立滑膜面：

　　接下来构造滑膜趋律，为了保证系统任意状态均使得误差e趋近滑模面，并且沿着滑模面运动到原点。意味着系统动力学将渐近地跟踪期望的轨迹，使得整个过程保持滑膜特性，保证机械臂系统的平稳运行，提高机械臂系统的鲁棒性。对式子（7）求导得到趋近律：

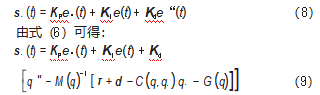
　　使得扰动和未建模动力学的向量d=0，求得s.(t)=0的解是为了在模型下达到期望的性能，称为期望控制力矩[13，15]，得到τeq：

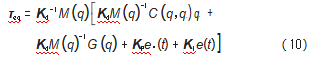
　　在实际控制中，很少会出现系统保持零状态的情况，这可能引发系统的振荡现象。这种抖振行为可能会破坏系统原本良好的性能，导致系统内未建模的高频振动，增加能量消耗，进而对机械系统造成严重损害，因此需要设计辅助控制力矩(τr），消除不良扰动的影响。因此设计李雅普诺夫函数为：

　　根据李雅普诺夫第二定律可知，若系统稳定则V<0，根据以上式子，则滑模控制律由期望控制律和辅助控制律组成，由式（12）表达：

　　通过李雅普诺夫证明系统的稳定性，求解李雅普诺夫方程，得到辅助控制律(τr）的形式，由式（13）得：

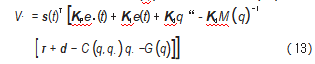
　　根据李雅普诺夫第二定律，V<0时系统是稳定的，于是滑膜控制律为：

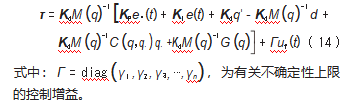
　　模糊逻辑系统的输出可由式（15）表达[11]：

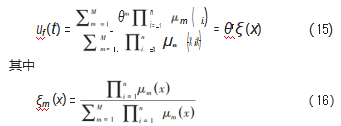
　　式中：θ为可调参数；ξ(x)为模糊基函数向量；M为模糊规则数量；μm(xi)为模糊集合m的隶属度函数。

　　将式（14）代入式（13）：

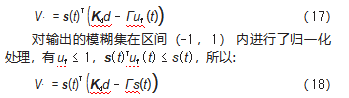
　　选择Γ>Kdd，则V.<0即到达控制实际上实现了一个稳定的滑模控制系统，因此求得τr并且γn需要满足式（19）：

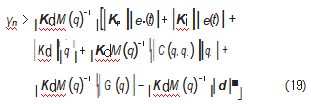
　　由于V.<0，所以当t→∞时，系统渐近稳定，运动轨迹从初始时刻滑到滑模面s(t)=0。

　　3仿真实验

　　本文在MATLAB仿真平台上建立了一个双臂机器人的运动模型，并使用Robotic Toolbox进行机械臂动力学等数学方程的计算。通过在MATLAB中创建了一个UR5双机械臂的模型，并设置了机械臂的参数。通过章节2的运动学闭链约束，对双机械臂建立了闭链约束，使得双机械臂能够协同运动，保持运动的一致性。其中，赋予双机械臂中任一机械臂末端运动轨迹，通过闭链运动学约束可知另一机械臂的运动轨迹，同时通过ikine函数可知机械臂的6个关节处的角度。

　　本文通过使得双机械臂在两种不同的滑模控制下，运行一个复杂轨迹，并且使得机械臂的姿态不变。将传统的滑模控制与本文的滑模控制进行对比，验证本文的模糊滑模控制的性能优于传统滑模控制，传统滑模控制控制律为：

　　设计建立任一机械臂如下末端运动轨迹方程：

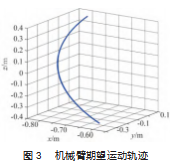
　　根据UR5机械臂参数在MATLAB中建立双臂机器人运动模型如图2所示，其运动轨迹如图3所示。

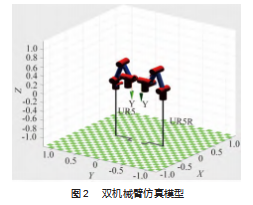
　　通过UR5机械臂的关节质量m、质心向量r、黏性摩擦Bm、电机惯性Jm和齿轮传动比G来计算机械臂的任意时刻下的惯性矩阵M(q)，离心力和哥式力矩阵C(q,q.)，重力矩阵G(q)。参数如表1所示。

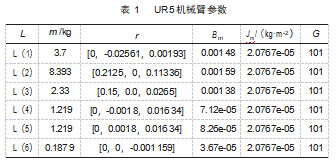
　　通过上述参数通过Robotic toolbox求得UR5机械臂在任意时刻的惯性矩阵M(q)，离心力和哥式力矩阵C(q,q.)，重力矩阵G(q)，设置当q=[1 2 3 4 5 6]，且q.=[0.1 0.1 0.1 0.1 0.1 0.1]。其求得的M(q)，C(q,q.)，G(q)如下：

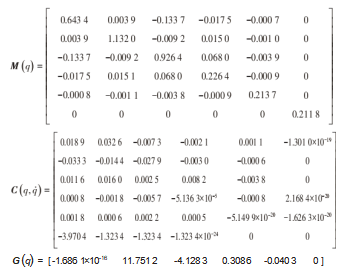
　　通过上述获得的参数可知UR5机械臂的动力学方程成功建立，并且通过求得的惯性矩阵M(q)，离心力和哥式力矩阵C(q,q.)，重力矩阵G(q)方程带入到UR5动力学方程中，通过本文提出的模糊滑模控制策略，设立的期望轨迹和外部干扰，对UR5机械臂进行仿真实验，所得到的滑模控制轨迹跟踪结果如图4所示，机械臂关节的控制输入如图5所示。在仿真实验图中，实线代表期望轨迹，虚线代表实际轨迹。

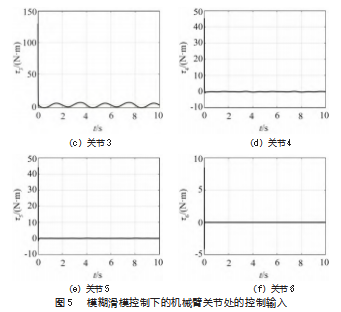
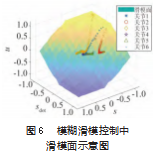
　　由图4可以观测到机械臂关节处对于期望轨迹跟踪的误差。在模糊滑膜控制下，机械臂关节的轨迹跟踪效果良好，由图可知，模糊滑模控制在各个关节处的轨迹跟踪误差都逐渐趋于0，并且消除了震荡，保持双机械臂的鲁棒性。图5可以观测到机械臂关节处的控制输入力矩。经过模糊滑模控制下的机械臂输入力矩能够快速的趋近于0，同时消除了震荡，维持了双机械臂系统的稳定性，提高系统的鲁棒性。同时实验中给予了关节1~3不同的外力干扰，由图4（a），4（b），4（c）可以看出模糊滑模控制在外力的干扰下能够良好地完成轨迹跟踪。通过图6可以直观地观测到本文所设计的关节1~6处的控制律在滑模面上的状态。

　　4结束语

　　为了验证本文提出的控制策略的可行性与有效性，本文通过MATLAB与Robotic toolbox作为仿真实验的基础，通过建立双机械臂系统的闭链约束，保持多机械臂之间的同步性。基于PID控制和模糊控制建立本文的模糊滑模控制算法。本文通过模糊滑模控制与传统滑模控制的对比仿真实验，得出模糊滑模控制使得机械臂在进行轨迹跟踪时遇到外部干扰能够更加快速收敛并且趋于稳定。最后通过建立双机械臂系统与运动轨迹，双机械臂通过闭链约束进行同步运动，同时通过模糊滑模控制完成了对期望轨迹的跟踪，使得双机械臂系统能够进行协同运动。通过以上实验结果证明了提出基于模糊滑模控制的双6-DOF机械臂协同控制策略可以有效地提高机械臂收敛速度与轨迹跟踪误差，同时有效抵抗内外部扰动以及消除力矩的震荡。本文控制策略保持了双机械臂的协同性和鲁棒性。

　　参考文献：

　　[1]冯春成,刘满禄,张华,等.工业机器人机械臂加工目标定位控制研究[J].计算机仿真,2017,34(6):319-324.

　　[2]李爱民,王启广.基于改进模糊滑模控制的机械臂运动轨迹仿真[J].中国工程机械学报,2018,16(2):115-119.

　　[3]郑涛,刘满禄.一种机械臂分段插值轨迹规划方法[J].机械设计与制造,2020(3):261-264.

　　[4]OHRI J,DEWAN L,SONI M K.Tracking control of robots using decentralized robust PID control forfriction and uncertainty com⁃pensation[J].Lecture Notes in Engineering&Computer Science,2007.2167(1):2047-2053.

　　[5]李贺立,杨冬,杨德志,等.基于阻抗控制的双臂机器人协调搬运方法研究[J].机床与液压,2017,45(21):64-67,91.

　　[6]王会方,朱世强,刘松国.具有H∞跟踪性能的机器人自适应PID控制[J].控制与决策,2009,24(10):1585-1588.

　　[7]邢艳荣,秦佳伟,苏彩云.基于自适应滑模控制的四轮全向移动机器人轨迹跟踪方法研究[J].机械传动,2015(12):39-43.

　　[8]范兴民,王启志.神经网络自适应滑模控制的不确定机器人轨迹跟踪控制[J].微型机与应用,2012,31(9):60-62.

　　[9]HOU Zhongsheng,JIN Shangtai.Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems[J].IEEE Transactions on Neural-Networks 2011,22(12):2173-2188.

　　[10]PENG L I,SUN W M,LI W Q,et al.Application of improved in⁃tegral sliding surface to flight control system[J].Control Engi⁃neering of China,2010.

　　[11]鲁丙涛.机械臂的滑模控制算法研究[D].洛阳:河南科技大学,2018.

　　[12]郑华辉,方宗德.基于自适应神经网络控制的机械臂运动轨迹跟踪误差研究[J].机械设计与制造,2019(6):139-141,145.

　　[13]DEVIKA K,THOMAS S.Sliding mode controller design for MI⁃MO nonlinear systems:a novel power rate reaching law ap⁃proach for improved performance[J].Journal of the Franklin In⁃stitute,2018,355(12):5082-5098.

　　[14]EKER I.Sliding mode control with PID sliding surface and ex⁃perimental application to an electromechanical plant[J].ISA Transactions,2006,45(1):109-118.

　　[15]张金萍,刘阔,林剑峰,等.挖掘机的4自由度自适应模糊滑模控制[J].机械工程学报,2010,46(21):87-92.

　　[16]SOLTANPOUR M,OTADOLAJAM P,KHOOBAN M.Robust control strategy for electrically driven robot manipulators:adap⁃tive fuzzy sliding mode[J].IET Science,Measurement&Tech⁃nology,2015,9(3):322-334.

　　[17]HE W,CHEN Y,YIN Z.A daptive neural network control of an uncertain robot with full-stateconstraints[J].IEEE Transactions on Cybernetics,2017,46(3):620-629.

　　[18]SPURGEON S K.Choice of discontinuous control component for robust siding mode performance[J].International.Journal of Control,1991,53(1):161-179.

　　[19]谢心如.六自由度机械臂阻抗控制方法研究[D].哈尔滨:哈尔滨工程大学,2018.

　　[20]王晓峰,李醒,王建辉.基于无模型自适应的外骨骼式上肢康复机器人主动交互训练控制方法[J].自动化学报,2016,42(12):1899-1914.