摘要：由于冷冻干燥机矩形干燥舱结构设计采用简化计算与经验设计相结合，为了满足其工作需求，在设计过程中确保安全性，常会出现过度设计的问题。针对该问题，本次研究采用迭代设计优化结构，使其既能满足抽真空阶段干燥舱变形量不得高于3 mm的要求，又能降低干燥舱自重、减少材料浪费以此降低成本，提升竞争力。优化过程中，将干燥舱三维模型进行优化，利用有限元分析法，对工作过程中抽真空阶段以及预冷却阶段干燥舱变形情况进行分析，明确后续优化只要满足抽真空阶段箱体所受应力即可满足冷却阶段工作需求。经多次迭代优化结构，其变形量最终降到2.951 mm，质量减少417 kg。该研究结果对设计人员进行冷冻干燥机矩形干燥舱强度结构设计时，提供加强筋排布参考依据。

　　关键词：冷冻干燥机矩形干燥舱；有限元分析；结构优化

　　0引言

　　冷冻干燥机最初应用在食品、标本保存中，1909年引入医学领域，将生物制品、蛋白质采用盐冰预冻，真空状态下将硫酸用作吸水剂，这是冷冻干燥机的雏形。1935年世界上第一台商用冷冻干燥机问世，它主要应用于医疗药品的冷冻干燥[1]，自此以后冷冻干燥技术不再只停留于实验室的科学研究。1940年冻干人血浆进入市场，并迅速发展。国内在20世纪70年代生产制造冷冻干燥机，经不断地提升，1995年开始，满足药品生产的冷冻干燥机开始大规模投入使用。当前我国冷冻干燥机正在积极探索基于数字孪生技术的设计应用，以此提升设备的维护效率[2]。冷冻干燥产品的品质则是通过提升冷冻干燥技术以更好地保留产品内部生物活性化合物[3]。

　　冷冻干燥技术是利用低温低压的传热传质机理[4]，先将物料中的水冷冻至凝固点以下，使其转为冰，然后真空下升华成水蒸气达到干燥的目的[5]。通过该技术可以提高产品的质量和储存期限，并降低了储存条件，最大限度的保存蛋白质品质、食品中的各类营养物质，易于运输、储存和使用。因此现在被广泛应用在医药、食品工业、农产品深加工等领域[6]。冷冻干燥机是应用冷冻干燥技术，将物料中的水在低温低压条件下转移，从而实现产品干燥的设备。可以看到在各领域，它的应用都越来越广泛、深入。但是冷冻干燥机存在着成本高的缺点，无论是前期投资费用还是后期设备运行费用都较高。卢海山等[7]采用U型加强筋应用在冷冻干燥机矩形容器加筋封板上。杜建邦[8]通过刚度等方面的研究分析，提出轻量化设计，进行设备整体减重优化。

　　压力容器设计中，GB150—1998《钢制压力容器》针对抗拉强度安全系数，由规定的3.0降至GB/T150—2011《压力容器》中规定的2.7，安全系数的降低不仅可以提高产品的竞争力，也可以为节能减排奠定基础[9-10]。轻量化是提升设备的必要途径，提升轻量化可以从结构优化、材料优化、制造工艺优化3个方面进行[11]，由于材质以及制造工艺优化所需研发周期长，且研究结果投入实际生产也需要大量时间去验证其可靠性。因此，本次研究从结构优化入手，针对冷冻干燥机矩形干燥舱以及加强筋进行分析研究，使其在满足工作状态的条件下，也为其实现轻量化目标提供可供参考的思路。

　　1有限元分析法

　　冷冻干燥机矩形干燥舱的设计过程中，为了确保安全，设计人员根据设计经验或现有设备进行设计。用该方法设计出的产品虽然安全性毋庸置疑，但箱体的强度过大，致使出现原材料浪费、设备成本过高的问题。因此采用有限元分析法，分析现有冷冻干燥机的箱体强度，为其结构优化提供参考方向[12]。

　　有限元分析法是一种数值分析方法，用于计算仿真复杂的结构、构件及其变形和应力情况的方法。该方法基于有限元分析理论，将任何形状的结构分解成许多个小单元，然后通过数学计算方法分析每个小单元内的应力、位移和它们之间的相互作用，进一步得到整个结构的性能。其运算过程如下[13-14]。

　　（1）几何体的结构离散化

　　有限元法是将几何体离散为若干个单元[15]，这些单元相互连接且没有重叠。进而将这些单元和节点编号、标出坐标。

　　（2）几何体单元位移函数

　　根据位移与坐标间的关系，确定单元位移函数，则任意单元中点的位移都可以用式1进行求解[16]：

　　式中：{u}为任意点的位移列阵；[N]为函数矩阵；{δ}e为单元内点的位移列阵。

　　（3）单元力学性能分析

　　分析单元的力学性能，可根据单元中点的位移方程，用式（2）得到单元应变：

　　式中：{ε}是单元中点的应变列阵；<B>是几何矩阵；{δ}为几何体节点位移列阵。

　　根据应力和应变间的关系，由式（3）得到单元应力：

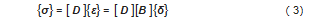
　　式中：{σ}是单元中点的应力列阵；[D]是材料的弹性矩阵。

　　根据单元节点位移和等效节点载荷间的计算式，得到单元节点力与位移间的关系：

　　式中：{f}是单元等效节点载荷；[K]e是刚度矩阵。

　　（4）建立几何体结构平衡方程

　　应用刚度集成法，将单元刚度矩阵、单元等效节点载荷列阵组合为几何体整体的刚度矩阵、载荷矩阵，以此建立整个几何体离散结构的平衡方程：

　　式中：{F}为几何体载荷列阵；[K]为几何体刚度矩阵。

　　（5）求解

　　根据降阶法等给平衡方程引入位移边界条件，使其具有唯一解，进而可以得到所需的单元应力和应变。

　　2冷冻干燥机简述及结构分析

　　冷冻干燥机由外壳、真空室、水捕集器、压缩机、真空泵、制冷机等构成，其工作过程主要为五个步骤：预冷却、抽真空、真空干燥、提升温度以及等待和抽真空[17]。预冷却是将待冻干产品置入冷冻干燥机矩形干燥舱，通过温度控制降温到冻结点以下，以便将其冷冻。然后利用真空泵，对真空室抽真空，建立真空环境。气闸阀关闭后，真空泵继续工作，使更多的水蒸气可以升华，以去除物品中更多的水分。本次研究冷冻干燥机矩形干燥舱及其外部加强筋在经历抽真空和提升温度过程中箱体受力以及产生形变的情况，判断加强筋是否满足箱体需要。

　　2.1结构形式和载荷分布
　　2.1.1矩形干燥舱结构

　　虽然圆筒形冷冻干燥机具备承受压力大、易于生产制造、成本低廉的优势，但其空间利用率较六面体形利用率低，在六面体形干燥舱结构下可通过减小冷阱与制冷系统间的距离，提升其效率。经综合考虑选用六面体形冷冻干燥舱，结构形式如图1所示。

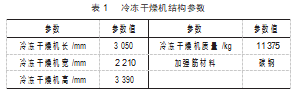
　　箱体顶部应用工字钢与加强板，左侧及背面采用加强板，右侧应用工字钢起支撑作用。模型的主要尺寸和相关参数如表1所示。

　　2.1.2载荷分布

　　为确保舱体在工作过程中的稳定性，需对其进行强度计算模拟。首先需要明确其工作条件有助于精确模拟模型的受力情况，达到更准确地预测模型结果的目的[18]。

　　冷冻干燥机矩形干燥舱在预冷却阶段仅受大气压力；抽真空阶段，箱体顶端受到来自顶部液压缸的工作压力，整个箱体受到大气压力；加热阶段箱体内部受到0.15 bar（1 bar≈0.1 MPa）的正压力。

　　2.2力学模型简化及有限元分析
　　2.2.1力学建模原则

　　进行有限元网格划分前，需要对模型进行简化处理[19-20]，提升有限元分析的准确性，并在更短的时间内获得更精确的分析结果。

　　（1）设定干燥舱模型上加强筋之间的约束关系，确保分析结果准确。

　　（2）检查冷冻干燥机干燥舱模型的几何特征并调整、补全存在缺损、破角的部位。

　　（3）将模型进行细化和修正，以提高模型的计算效率。其中包括删除不必要的组件、优化舱体模型以及修正舱体与部分加强筋间存在的空隙。

　　2.2.2有限元分析

　　将模型导入有限元软件中，为模型添加材料属性，根据模型特征选择划分网格的类型、网格的疏密，为冷冻干燥机模型施加其在工作状态中受到的压力，然后进行有限元分析。由于加强筋材料为碳钢，弹性模量E为200~210 GPa，泊松比ν为0.25~0.33，抗拉强度σb为370~500 MPa，屈服强度为235。经过网格划分后将抽真空阶段，箱体顶端受到的工作压力，整个箱体受到的大气压施加到模型上，得到箱体各部分变形量，结果如图2所示。可以看到箱体最大变形量为18.19 mm，且变形集中在箱体顶端。显然，此变形量过大，长期使用会产生安全隐患，需优化结构。

　　在预冷却阶段，舱体仅受大气压力，将其施加至箱体模型，得到箱体变形量如图3所示。根据结果可知，在该阶段形变量最大位置处于箱体左侧，且形变量为0.712 mm。

　　因此，后续结构优化仅需模拟抽真空阶段，使得箱体形整体变量降低至3 mm即可。

　　3冷冻干燥机矩形干燥舱结构迭代优化

　　根据GB/T150—2011《压力容器》强度设计标准中矩形截面容器强度计算方法仅可得到加强筋间距的范围值，在实际应用中，一般则采用简化计算与经验设计相结合，但该方法的准确性不够，常会出现材料用量大，结构设计较为谨慎，与同规格产品相比质量大、成本过高、产品竞争力降低。因此，本次研究在已有冷冻干燥机矩形干燥舱结构的基础上，借助有限元分析应用迭代设计，将箱体变形量降低至3 mm内，提升干燥舱安全性。

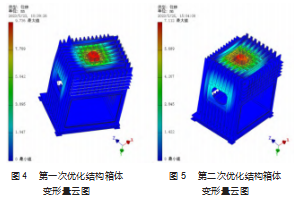
　　通过分析图2可知抽真空阶段，箱体最大变形量完全集中在箱体顶端，而顶部液压缸组件并没有加强筋分散其应力，因此以液压缸中心为最强受力点增设圆形加强筋，其质量为10 442 kg，得到如图4所示的结果。可知，此时箱体形变依然集中在顶部，且变形量为9.736 mm。该结果虽降低46.5%的形变量，但通过干燥舱形变位移分析云图可知，液压缸顶部所受的应力依然过大，且形变量依然不满足要求，需再次分散顶部所受应力。

　　通过观察箱体顶部加强筋变形云图可知，工字钢受力云图集中，且工字钢与加强板连接处变形量应在2 mm左右，则该加强方式也不能满足需要，考虑将顶部加强筋都替换为工字钢以降低顶部变形量。

　　第二次优化是将工字钢布满顶部且继续采用井字形排布方式，液压缸顶部加强筋与工字钢接触，以分布顶部应力，增强顶部强度。根据变形云图5可知，此时最大变形量依然集中在顶部，但应力有所分散，且最大变形量为7.112 mm，但变形量仍不满足需要。需再次增强箱体强度。

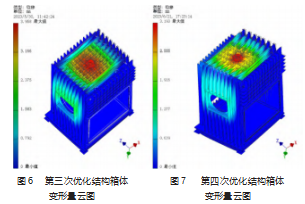
　　根据前两次优化云图可看出，仅以液压缸中心为最强受力点增设圆形加强筋变形量依然不能满足需要。此时考虑进一步通过增设加强板在其上再次使用圆形加强筋分散顶部应力，其质量为10 987 kg，得到的结果如图6所示，顶部最大变形量为3.958 mm。

　　由于顶部加强筋强度不满足需求，第4次优化则将顶部工字钢替换为25号工字钢其质量为10 896 kg，此时箱体顶部变形量为3.514 mm。通过进一步增加顶部井字形加强筋的排布，形变量也仅减小至3.218 mm。再一次通过扩大液压阀的加强板长度，使得应力能分散至两端的工字钢，顶部变形量减小至3.193 mm，如图7所示，该结果依然不满足需求，因此考虑再次替换工字钢型号。

　　本次优化顶部全部替换为28号工字钢，由于28号工字钢高度已十分接近液压阀高度，将顶部加强板高度增加至液压阀底端，此时箱体形变量为3.176 mm，显然，井字形加强筋必不可少。通过有限元分析，该种形式箱体顶部形变量为3.089 mm。

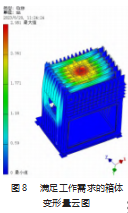
　　由于井字形加强筋是以液压阀为圆心层层排布，箱体顶部两端工字钢分散的应力较少，因此，在箱体轴线上再次增设两个加强筋，箱体质量为10 958 kg，如图8所示，其有限元模拟结果：箱体顶部变形量为2.951 mm，箱体质量减少417 kg。该结果满足冷冻干燥机矩形干燥舱工作要求。

　　4结束语

　　本文借助有限元分析研究在冷冻干燥机工作过程中抽真空阶段箱体在受到来自液压缸的压力、大气压力时，根据箱体变形量通过迭代设计优化箱体顶部结构，使其最大变形量满足3 mm工作要求。根据优化结果可知：（1）箱体顶部与液压缸接触，因此受到的应力较大，在该种情况下，采用井字形工字钢排布方式尽可能将应力分散，才能最大限度的降低箱体顶部变形量；（2）当箱体变形量不能满足工作需求时，考虑采用更高规格的加强筋而非通过增加加强筋数量降低其变形量，以此既可以提升箱体自身安全性的，又可以降低加强筋用量、降低冷冻干燥机的自重、提升经济效益。本次研究也可为冷冻干燥机结构提供后续研究方向：根据结果可知，箱体侧面强度不仅满足工作需求，且有一定余量，可考虑后续进一步优化侧面结构，使其既满足工作需要，又能降低成本。

　　参考文献：

　　[1]胡新卓.Ray125型真空冻干机设计[D].上海:华东理工大学,2017.

　　[2]王磊.数字孪生技术在冻干机智能化中的应用探索[J].化工与医药工程,2023,44(1):51-55.

　　[3]PANI A,SHIRKOLE S S,MUJUMDAR A S.Expert reviews for assessment of recent developments and future prospectives of global drying r&d[J].Drying Technology,2023,41(3):335-338.

　　[4]陈洲.FD50型真空冻干机设计[D].昆明:昆明理工大学,2022.

　　[5]王艳艳,张渺.冻干机箱体极限真空升高原因分析[J].价值工程,2020,39(14):203-204.

　　[6]沈晨.真空冷冻干燥机中螺杆式制冷压缩机的应用[J].南方农机,2018,49(20):70,103.

　　[7]卢海山,龚曙光,张丽娜.冻干机矩形容器加筋封板的有限元分析研究[J].化工装备技术,2018,39(5):6-10.

　　[8]杜建邦.某电动汽车有限元分析与轻量化设计[D].淄博:山东理工大学,2020.

　　[9]陈玮玮.基于有限元的电梯轿架强度分析及其结构优化[D].杭州:中国计量大学,2020.

　　[10]胡耀增.基于有限元分析法的复合材料球头销成型过程仿真优化——评《压力容器全模型ANSYS分析与强度计算新规范》[J].压力容器,2019,36(11):80.

　　[11]才胜,罗颖辉,李青林.农业机械轻量化技术研究现状与发展趋势[J].机械工程学报,2021,57(17):35-52.

　　[12]许艳霞,刘蓓.有限元分析法在工程机械零部件设计中的应用[J].内燃机工程,2023,44(2):111.

　　[13]张淇.巴哈越野赛车骨架的有限元分析及轻量化设计[D].青岛:青岛大学,2020.

　　[14]龙顺.新型无门架衬砌台车有限元分析及优化设计[D].长沙:湖南师范大学,2020.

　　[15]曹磊.某纯电动客车车架设计及有限元分析[D].苏州:苏州大学,2019.

　　[16]王贺明.机床装配体结构有限元分析[D].沈阳:沈阳工业大学,2018.

　　[17]梁艳英,魏冬梅,张莉.大型仪器共享系统中冻干机的开放使用与维护[J].安徽农业科学,2013,41(7):3287-3288,3290.

　　[18]高宇航.地铁转向架构架有限元分析与强度试验[D].长春:吉林大学,2022.

　　[19]郭鹏程.新型打桩机工作装置有限元分析与优化设计[D].西安:长安大学,2022.

　　[20]杨国营.基于概念设计的汽车轮毂轻量化设计[J].机电工程技术,2023,52(6):257-262.