摘要：本文采用FLUENT软件对T型微通道内气液两相Taylor流进行模拟，得到了各物理参数对Taylor流的影响规律。在此基础上，采用最小二乘法进行拟合，得到了可以更准确预测T型通道内气液两相Taylor流气泡和液柱长度的经验关联式。

　　关键词：T型微通道；Taylor流；气液两相；最小二乘法

　　0引言

　　近年来，微化工设备与过程被公认为是化学工程学科发展的新方向之一。微通道反应器由于其通道尺寸在亚微米到亚毫米数量级，比表面积可达10 000~50 000 m2/m3，而常规反应器比表面积一般低于1 000 m2/m3[1]，因而具有很好的传质、传热能力，可大幅度提高能源的利用率。

　　微通道内气液两相流流型是研究传质传热的基础[2]，它对压降、传热速率等都有很大的影响。与其他流型相比，Taylor流不仅操作区域宽，还具有轴向返混小、径向混合好等优点，被认为是最适合气液两相反应的流型。因此，本文对微通道内的气液两相Taylor流进行分析研究。

　　1物理模型

　　资料表明[3]，在亚毫米及毫米尺寸下的圆管中，二维和三维模型中气泡长度差别很小，本次模拟选用二维模型。

　　图1为T形微通道，微通道包括二个垂直进口和微通道主体。水和空气分别从入口处进入，然后进入微通道主体。截面尺寸均为d，混合区长6d，反应区域为30d，整个系统在常温常压下，表观气速为0.02~0.25 m/s，表观液速为0.05~0.1 m/s，微通道的圆管直径为0.25~1 mm。大量研究表明[4-7]，在此条件下发生Taylor流。

　　2数值模拟

　　对非稳态的气-液两相流，VOF模型是唯一的可以确定清晰界面的多相模型，为了观察气液界面，本文采用Fluent软件的VOF模型模拟T形微通道中的Taylor流。

　　采用GAMBIT软件对T型微通道进行网格划分，通过对网格无关性进行验证，最终采用当量直径的1/20的网格进行计算。

　　2.1模拟假设

　　对T形微通道Taylor流流动过程进行数值模拟，做出以下假设：由于微通道截面尺寸非常小，雷诺数一般小于2 000，认为微通道内流体为层流状态；模拟过程中设温度是恒定的，气液两相物性组成视为恒定的，混合物性质只与其组成有关；考虑到微通道内的压降比较小，认为气体和液体是不可压缩流体，即密度为不变的；由于邦德数小于1，模拟时忽略重力的作用。

　　2.2初始条件和边界条件

　　在开始计算之前，对流场初始化，初始时整个微通道内充满液体，各个单元速度为0，表压均为0 Pa，气、液两相分别由两个进口进入，混合后由出口流出，出口为压力出口，为1 atm，壁面采用无滑移边界条件。

　　选用二维非稳态进行求解计算，采用PRESTO算法对压力进行差值计算，以及PISO算法对压力-速度耦合方程求解，用二阶迎风格式（second-order up-wind）求解动量方程，以及几何重构方案（the geometricreconstruction scheme）处理气液界面附近的差值，为了减小非物理性的压力振荡对液膜速度场稳定性的影响，选用Green-Gauss node-based算法对网格的节点处各个标量的值进行计算。选用默认的松弛因子，适当调整时间步长以保证收敛。

　　3计算结果分析及讨论

　　气泡长度作为Taylor流流型的一项重要指标，可体现通道内气体的分布情况。本文通过大量的模拟来探究气液表观流速、通道直径、液相性质对气泡和液柱长度的影响。

　　3.1气液表观流速对Taylor流的影响

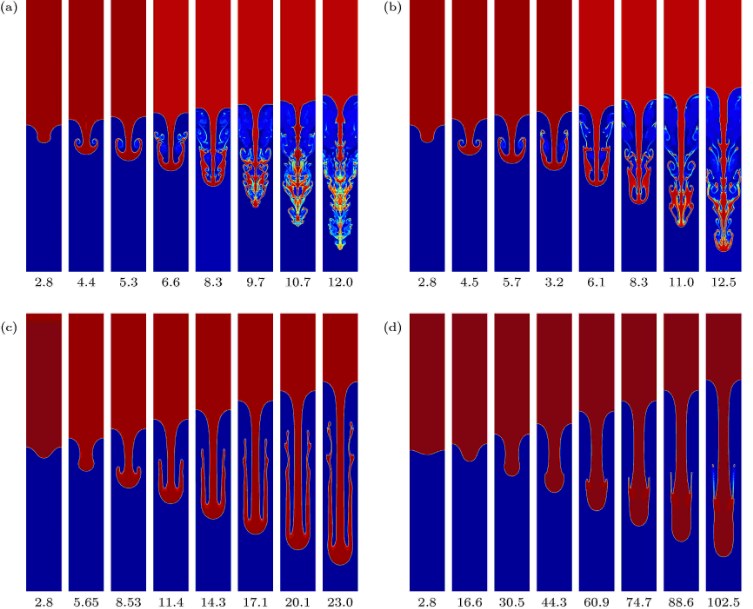
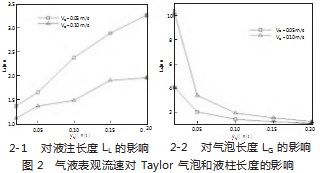
　　为了研究气液表观流速对Taylor流型的影响，在直径为0.5 mm的微通道内进行模拟分析，当气体表观流速vG分别为0.05、0.1 m/s时，液体表观流速vL分别为0.02、0.05、0.10、0.15、0.20 m/s时，得到气泡长度LG和液柱长度LL如图2。当气相表观流速相同时，液柱长度随液相表观流速的增加而增加，而气泡长度随之减小；当液相表观流速相同时，气泡长度随气相表观流速的增加而增加，液柱长度随之减小。

　　3.2通道直径对Taylor流的影响

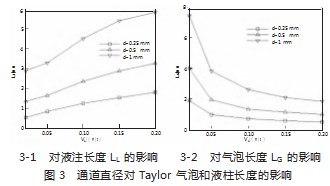
　　为了研究通道直径对Taylor流型的影响，选取直径d为0.25、0.5、1.0 mm的微通道进行仿真分析，当气体表观流速vG为0.05 m/s，液体表观流速vL分别为0.02、0.05、0.10、0.15、0.20 m/s时，得到气泡长度LG和液柱长度LL如图3。从图3中看出，当气液表观流速相同时，增加通道直径，气泡和液柱长度随之增加，这是由于在较小的通道中，黏性力和表面张力的影响比较显著，气相更易形成小气泡，而且通道内的压降也相应较大，这些因素共同作用导致气泡长度和液柱长度均较小。

　　3.3液相性质对Taylor流的影响

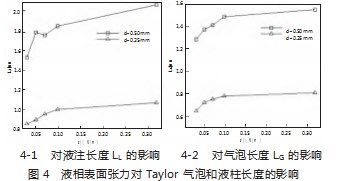
　　为了研究流体黏度和表面张力性质对对Taylor流的影响，当通道直径d分别为0.25 mm和0.5 mm时，气相表观流速vG为0.1 m/s，液相表观流速vL为0.15 m/s时，假设具有相同黏度μ=0.000 92 Pa·s，表面张力σ分别为0.032、0.052、0.072、0.1、0.32 N/m的5种流体，得到气泡和液柱长度如图4。

　　当通道直径分别为0.25、0.5 mm时，气相表观流速为0.1 m/s，液相表观流速为0.15 m/s时，假设了表面张力σ=0.072 N/m，黏度μL分别为0.000 1、0.000 5、0.000 92、0.001 9 Pa·s的4种流体，得到气泡和液柱长度如图5。

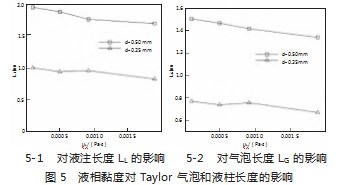
　　由图5看出，随着液相表面张力的增加，Taylor气泡和液柱长度均有所增加，这是因为表面张力较大的液体更容易聚在一起，使得液柱变长；液体内部分子对界面处液体分子作用力增加，从而液相对气相的挤压减弱，气相有机会形成更长的气泡。由图5还可看出，随着液相黏度的增加，Taylor气泡和液柱长度均略有减小。

　　3.4 T形通道内Taylor流气泡和液柱长度预测

　　通过模拟分析，发现气液表观速度、通道内径、液相表面张力和黏度对Taylor气泡和液柱长度有一定影响，忽略重力、接触角对气液柱长度的影响，气泡和液柱长度可用无量纲数表示为：L=L（Re，Ca，εG），使用origin软件通过自定义函数对曲线进行拟合[8]，得到气泡和液柱长度经验关联式如式（1）—式（3）：

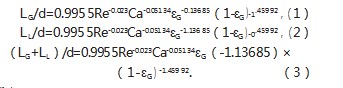
　　式中：0.2<εG<0.833，17.416<Re<1247，9.751×10-4<Ca<7.187 5×10-3，LG/（LG+LL）=εG，LL/（LG+LL）=1-εG。将拟合得到的经验关联式和模拟结果对比，得到图6，本次拟合的可决系数值达0.977 07，接近于1，说明拟合效果较好。由经验关联式看出，气泡和液柱长度主要受含气率的影响，毛细数和雷诺数影响作用较小，即在较宽的操作条件下，气泡与液柱长度变化不大。

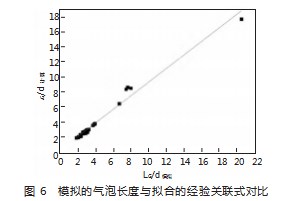
　　将本文拟合得到的经验关联式同Kawaji[9]的实验结果和Qian[3]提出的经验关联式对比，由于气泡长度受到含气率、雷诺数和毛细数的影响，当表观气速为0.079 m/s时，本文提出的关联式比Qian提出的关联式更接近于Kawaji[9]的实验结果；当表观气速分别为0.04 m/s和0.317 m/s时，部分预测结果比Qian的要好；当气相表观流速为0.317 m/s，液相表观流速为0.042 m/s时，预测结果与Kawaji[7]实验结果相差较大，其原因在于此时含气率(ε=0.883）超出了本文经验公式适用的含气率的范围（0.2<εG<0.833）。总的来说，在本文的提出的使用范围内，式（1）—式（3）可以较好地预测气泡长度、液柱长度和单元长度。

　　4结论

　　采用FLUENT软件中的VOF模型对微通道Taylor流的基本参数进行了数值模拟，得到了如下结论：

　　1）气相表观流速相同时，液柱长度随液相表观流速的增加而增加，气泡长度随之减小；当液相表观流速相同时，气泡长度随气相表观流速的增加而增加，液柱长度随之减小。

　　2）当气液表观流速相同时，增加通道直径，气泡和液柱长度随之增加。

　　3）随着液相表面张力的增加，气泡和液柱长度均有所增加；随着液相黏度的增加，Taylor气泡和液柱长度有所减小。

　　4）采用最小二乘法，得到了可以更准确的预测气泡和液柱长度的无量纲关系式，为微反应器的设计提供参考依据。

　　参考文献

　　[1]陈光文,袁权.微化工技术[J].化工学报，2003（4）：427-439.

　　[2]马友光，付涛涛，朱春英.微通道内气液两相流行为研究进展[J].化工进展，2007，26（8）：1068-1074.

　　[3]Qian D,Lawal A.Numerical study on gas and liquid slugs for Taylor flow in a T-junction microchannel[J].Chemical Engineering Science,2006,61(23):7609-7625.

　　[4]Chung P M Y,Kawaji M.The effect of channel diameter on adiabatic two-phase flow characteristics in microchannels[J].International Journal of Multiphase Flow,2004,30(7):735-761.

　　[5]Yang C Y,Shieh C C.Flow pattern of air water and two-phase R-134a in small circular tubes[J].International Journal of Multiphase Flow,2001,27(7):1163-1177.

　　[6]Coleman J W,Garimella S.Characterization of two-phase flow patterns in small diameter round and rectangular tubes[J].International Jour-nal of Heat and Mass Transfer,1999,42(15):2869-2881.

　　[7]Akbar M K,Plummer D A,Ghiaasiaan S M.Gas-liquid two-phase flow regimes in microchannels[C]//ASME 2002 International Mechani-cal Engineering Congress and Exposition.American Society of Me-chanical Engineers,2002:527-534.

　　[8]魏慧玲，王闪闪，普洁，等.Origin软件多自变量多参数曲线拟合功能探究[J].河南师范大学学报：自然科学版，2012，40（3）：38-40.

　　[9]Santos R M,Kawaji M.Numerical modeling and experimental investi-gation of gas–liquid slug formation in a microchannel T-junction[J].International Journal of Multiphase Flow,2010,36(4):314-323.