摘要：制造业等多个工业领域都大量使用旋转机械设备，机械故障可能会造成巨大经济损失甚至灾难性事故，但旋转机械发生机械故障的点位多，机械故障表象特征不明显，不易判断故障点位，采集旋转机械本体的振动信号，用于对旋转机械故障进行智能诊断极其重要。利用加速度传感器采集旋转机械4种状态(正常状态、基座松动、传动带破损和轴承破损故障)不同转速下的振动时域信号，在Matlab中进行多种信号特征量的提取，并以这些特征参数作为输入向量，建立SOM神经网络模型进行故障诊断，网络初始化需要用随机数设定输入层和映射层之间的权值初始值并对其进行归一化，形成输入层和竞争层组成的神经网络，其中竞争层也叫输出层，输入层神经元与竞争层的每一个神经元相联接，测试样本进入到SOM神经网络中的竞争层，会被与之映射最为强烈的神经元获得，即为获胜神经元，当输入新样本时，网络模型会以拓扑结构的形式输出分类结果。试验结果证明，SOM神经网络能够有效实现旋转机械故障的分类和诊断，判断旋转机械的故障位置。

　　关键词：旋转机械；振动信号；SOM神经网络；故障诊断

　　0引言

　　旋转机械设备占了机械设备的80%左右，实际工作中的旋转机械故障原因复杂，信号波动大，故障征兆与故障的关系具有不确定性。通过单一故障特征来进行诊断的传统故障诊断分析方法已经远远不能满足现代化机械设备的复杂故障诊断和快速智能识别的需求[1]。神经网络技术的应用为故障诊断问题提供了一种有效的解决途径，众多学者在这方面的研究取得了不少成果：葛宪福[2]通过对旋转机械典型故障的振动信号进行时域分析和频域分析，同时将其应用于实际工程中，并证明了仅仅依靠频谱分析对机械进行诊断会有误判的风险；王志永等[3]利用时域分析法中的波形诊断方法和数值分析诊断方法，根据振动信号的时域分析结果，得出了机床产生振动的原因；张津等[4]研究了旋转机械振动信号的故障诊断的特征值提取、图谱分析与故障树整理，并利用综合模拟试验台对常见的故障进行仿真试验，从而推导出故障的类型；苏剑飞等[5]研究了神经网络技术的基本原理及在旋转机械故障诊断中的详细应用步骤，

　　同时利用Matlab对BP神经网络模型进行了仿真，并验证了其准确性；汪庆华等[6]论述了RBF神经网络在旋转机械(风机)故障诊断中的准确性，从而避免了BP神经网络的缺点等。综上所述，通过提取振动信号波形进行分析来诊断，这种方法局限性极大，对于几种故障的波形差异不大的情况下难以判断；通过提取振动信号频域中的谱峰能量、提取时域和频域信号特征、提取机械的关键参数和利用小波分析和分型学结合的提取特征作为输入进行建模识别是比较有效的方法，但特征参数的提取过程较繁琐。

　　本文提出基于振动信号时域信号特征值作为输入向量，建立SOM神经网络模型对旋转机械进行故障诊断方法，实现在不拆卸的情况下，通过建立空间拓扑结构快速确定故障原因，且诊断模型具有自主更新性，有利于实际的应用，节省诊断维修成本。

　　1实验方案与样本数据的制取

　　1.1实验方案

　　本实验主要利用台钻机等高速旋转机械的表面振动信号进行特征参数提取，再根据SOM神经网络的无监督自组织竞争特性，建立诊断模型进行故障诊断，并对比了几种神经网络模型方法的优劣，实验具体方案如图1所示。首先，通过振动传感器采集不同故障状态下的振动时域信号，并将振动信号进行等长度截取，构成原始样本集。然后对样本集的每段振动时域信号进行时域分析，提取出与故障相关的表征参数，输入到SOM神经网络模型进行训练和测试[7]。

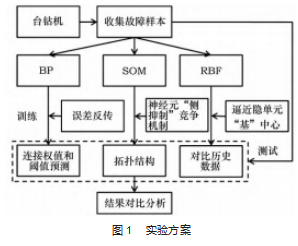
　　此外，为了验证SOM神经网络对旋转机械故障诊断的准确性和稳定程度，将其与具有反向误差传播的BP神经网络和以历史数据为基础的RBF径向基神经网络的诊断结果进行对比分析。

　　1.2样本数据的制取

　　利用加速度传感器采集微型台钻正常状态、基座松动、传动带破损、轴承破损故障等状态下的振动加速度信号。基座松动故障通过人为用扳手把基座的螺丝拧至其松动来设置。由于基座固定转轴，基座松动会使得微型台钻在运行时不平稳而导致振动信号的波动；传动带磨损故障通过人为磨损的传动带来设置。在微型台钻运行时，带轮带动传动带旋转，当遇到磨损的部位振动幅度变大；轴承破损故障通过敲打轴承内圈使其破损来设置。钻头随破损轴转动会造成振动信号的变化。故障设置具体如图2所示。

　　振动信号采集设备是ECON AVANT系列数据采集分析仪，设置采样率为6 400 Hz，采集空载低速的4种状态下Z轴方向上的振动加速度信号数据(共344 064点)，其时域信号波形如图3所示。

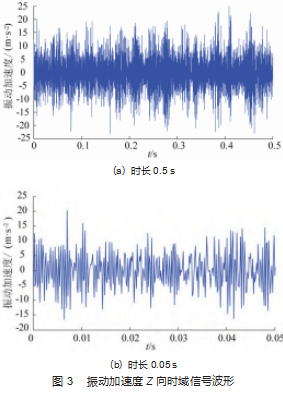
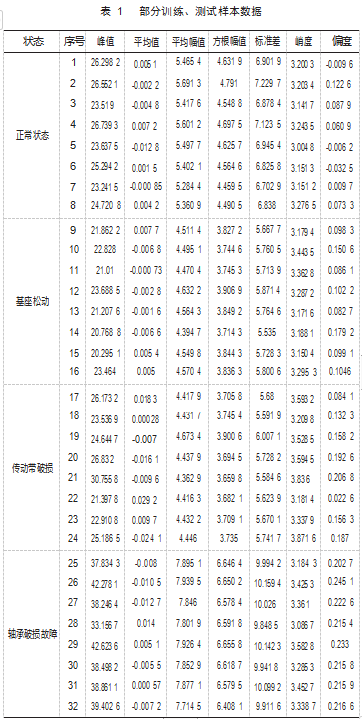
　　等间距选取每一种状态下的2 048个点作为一组，提取其时域信号峰值、平均值、平均幅值、方根幅值、标准差、峭度指标和偏斜度指标7个参数。一种状态选取130组，总共选取520组；其中，随机选取400组作为训练样本，120组作为测试样本，部分训练和测试的样本数据如表1所示。

　　样本分布具体如图4所示。从4种状态的数据分布情况可以看出，正常运行和轴承破损故障两种状态的特征样本差别较为明显，而基座松动和传动带破损两种故障状态的特征样本之间的差别较小。正常状态下的振动比较平稳，冲击变化小；基座松动和传动带磨损的振动信号变化很相似；轴承破损故障的振动信号变化最大，可见轴承故障对微型台钻的运行影响较大；正常状态与基座松动的偏度指标较小，而传送带磨损和轴承故障的偏度较大，可见后者不对称性大。

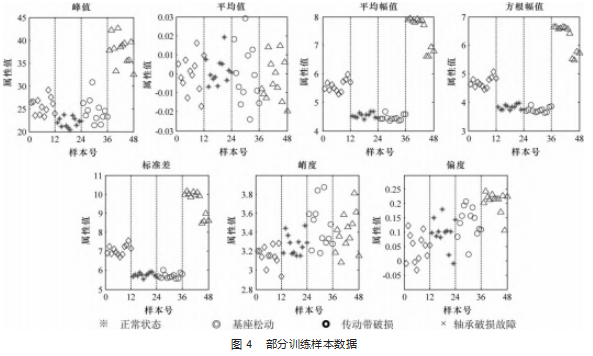
　　从表1、图4可以看出，不同特征的样本数值范围差别较大，而SOM学习算法会将样本尽量均衡地分配到各个类别去。因此，要样本数据进行归一化处理。采用mapminmax函数(xi0=xi-xmin/xmax-xmin)将数据归一化到[0,1]中。xi0为经过归一化后第i个数据，xi为原始第i个数据，xmin为第i个数据中的最小值，xmax为第i个数据中的最大值。

　　2基于SOM神经网络的故障诊断模型

　　SOM神经网络是由输入层和竞争层组成的神经网络，其中竞争层也叫输出层，其输入层神经元与竞争层的每一个神经元相联接，竞争层中每个神经元之间形成侧面联系，它们相互竞争[8]，如图5所示。

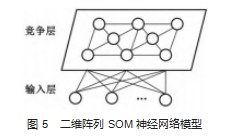
　　当测试样本进入到SOM神经网络中的竞争层，会被与之映射最为强烈的神经元获得，即为获胜神经元。当参与竞争的神经元数量越多，不同类型的样本之间的边界约明显，拓扑结构越舒展，甚至会出现更多的分类中心；反之，当参与竞争的神经元数量较少时，不同类型样本之间的边界越模糊，分类结果的随机性越大。

　　2.1 SOM神经网络的训练

　　SOM网络初始化需要用随机数设定输入层和映射层之间的权值初始值并对其进行归一化，m个输入神经元到输出神经元的连接权值被赋予较小的权值。网络模型的训练需要选取输出神经元j个“邻接神经元”的集合Sj，其中，Sj(0)表示时刻t=0的神经元j的“邻接神经元”的集合，Sj(t)Ct表示时刻t的“邻接神经元”的集合，区域Sj(t)随着时间的增长而不断缩小。

　　根据提取的7个时域信号特征数，输入层神经元节点个数为7个，输入向量为7维向量，即：

　　输入向量输入到映射层后，计算各神经元的权值向量和输入向量的欧式距离。映射层的第j个神经元和输入向量的距离，公式如下：

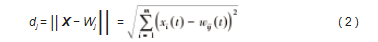
　　式中：wij为输入层的i神经元和映射层的j神经元之间的权值。通过计算，得到一个具有最小距离的神经元，将其称为获胜神经元，记为j*，并确定出某个邻域k，使得对于任意的j，

　　都有dk=min(dj)，得到邻接神经元集合，并修正输出神经元j*及其“邻接神经元”的权值∆wij：

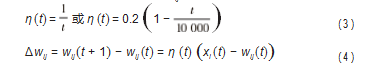
　　式中：η为一个大于0小于1的常数，随着时间变化逐渐下降到0。对于拓扑相关而形成的神经元子集，权重的更新是相似的。输出神经元Ok的输出值为：

　　SOM网络中神经元的拓扑组织就是它最根本的特征，输出神经元之间根据距离的远近决定抑制关系，最终使连接权值的统计分布与输入模式渐趋一致。当输入新样本时，网络模型会以拓扑结构的形式输出分类结果。训练结果分析如下。

　　本试验利用2×2基础网络结构对4种故障状态的振动参数数据进行自组织竞争运算，训练其聚类效果，如图6所示。4种状态的训练样本能均匀分布在4个竞争层神经元区域，故障的分类和识别有效，其类别中心点分布如图7所示。

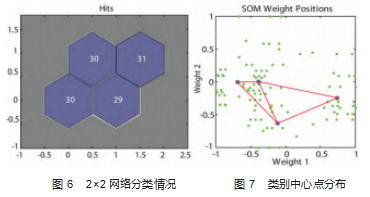
　　由此可见，样本被聚集到4个中心点，基座松动和传动带破损两种故障状态的类别中心点靠的比较近，而正常状态和轴承破损状态两个类别中心的相对疏远。为了更好地体现4种故障状态样本数据在SOM神经网络聚集情况和拓扑结构，通过反复尝试，当竞争层神经元的个数为7×7(二维)时，网络有较直观的诊断效果和较短的分类时间。

　　2.2 SOM神经网络的测试与结果分析

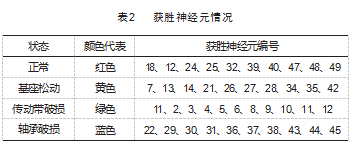
　　经过训练网络使其达到期望效果后，将测试数据输入到网络中进行识别分类，得到如图8、图9结果。从图8中可以看出，网络共有49个神经元；图9中颜色越深，代表相邻两个神经元之间的距离越远，越不可能是同一类型[9]。输出结果如图10、图11所示，每一组输出都会在获胜神经元相对应编号的位置上显示为1，其余都显示为0，诊断时间为1´57"。根据获胜神经元的分布情况，找出每一种状态下与其他状态不一样的神经元编码，即为该状态下的聚类结果。得到各种状态下的获胜神经元如表2所示。

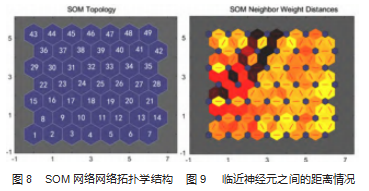
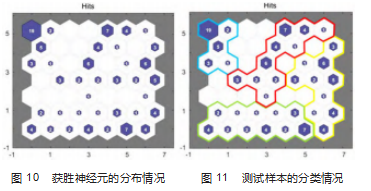
　　测试结果根据各状态下的获胜神经元的位置以及临近神经元之间的距离情况来判断的[10]，得到的结果如下。

　　(1)正常：3+2+2+6+4+7+4+1+1+1=31

　　(2)基座松动：3+1+6+3+2+5+1+1+4+4=30

　　(3)传动带破损：2+1+1+1+3+4+2+2+4+2+7=29

　　(4)轴承破损：19+2+5+3+1=30

　　因此，只有一组故障没有正确分类，正确率达到了99.17%，正常状态下、基座松动以及轴承破损状态下的识别正确率达到了100%，只有传动带破损故障的识别出现错误，正确率为96.67%。不管是与传递函数采用高斯函数，输出层传递函数采用线性函数[11]的RBF神经网络相比较，还是与沿误差性能函数梯度反向修改权值学习方法[12]的BP神经网络相比，其正确识别率都要高。

　　3结束语

　　SOM神经网络是模拟大脑神经系统自组织特征映射的功能，是一种竞争性学习网络，且在学习过程中能够无导师进行自组织学习。通过实验测试与分析可知，神经网络能够有效地诊断出故障类型，精度较高。SOM神经网络相比于BP神经网络和RBF神经网络更有优势，其最大特点是保持输入向量特征的拓扑结构不变，当输入向量比较相似时，它们相对应的输出神经元在输出层的位置也很接近，可以通过其空间位置来判断其故障类别，当SOM神经网络接受外界输入模式时，不同区域的神经元分工也会有差异，各区域对输入模式有着不同的响应特点，这个过程都是自组织完成的。除此之外，SOM神经网络不需要设置输出模式，需要的参数较少，通过无监督的形式进行故障分类和识别，更加方便快捷。

　　[1]龙舰涵.基于深度强化学习的旋转机械故障诊断策略[J].机械设计与制造,2021(10),288-294.

　　[2]葛宪福.振动信号分析在旋转机械故障诊断中的应用[D].北京:华北电力大学(河北),2007.

　　[3]王志永,杜伟涛,王习文,等.基于振动信号时域分析法的铣齿机故障诊断[J].科学技术与工程,2017,17(32):55-62.

　　[4]张津.旋转机械振动信号故障诊断研究[J].装备机械,2017(4):55-60.

　　[5]苏剑飞,赵捍东.神经网络在旋转机械故障诊断中的应用[J].微计算机信息,2007(13):214-215.

　　[6]汪庆华,王敬涛,邓东花.基于径向基神经网络的旋转机械故障诊断[J].现代电子技术,2010,33(18):141-142.

　　[7]杜灿谊,朱玉平,赖新方.基于传感器信号和神经网络的汽油机失火状态识别方法[J].小型内燃机与摩托车,2012,41(3),65-69.

　　[8]唐刚,姚小强,胡雄.基于SOM神经网络的岸桥起升电机状态聚类分析[J].东华大学学报(自然科学版),2018,44(4):595-601.

　　[9]张全德,陈果,林桐,等.基于自组织神经网络的滚动轴承状态评估方法[J].中国机械工程,2017,28(5):550-558.

　　[10]汪开正,黄亦翔,张旭东,等.基于AdaBoost-SOM方法的电机故障诊断[J].机械设计与研究,2019,35(2):155-159.

　　[11]薛萍,郝鹏,王宏民.基于径向基神经网络的新型齿轮故障诊断方法研究[J].控制与决策:2022,37(2),409-416.

　　[12]李雯,喻菲菲,杜灿谊,等.基于BP神经网络与概率神经网络的汽车发动机故障识别方法及对比分析[J].小型内燃机与车辆技术,2020,49(5):78-83.