摘要：针对结构化道路下自动驾驶车辆实时路径规划存在路径不稳定、曲率不连续、运算时间长等问题，提出一种基于二次的路径规划算法。从全局离散的导航路径中截取一段做平滑处理，构建Frenet坐标系；在离散的SL空间中用动态规划对车道内的障碍物做绕行决策，从而开辟可行驶区域；利用二次规划从可行驶区域中构建以安全性和舒适性评价指标为核心的代价函数，评价规划路径成本，选择能够最小化代价的最优路径。通过MATLAB/Simulink搭建算法框架，仿真实验结果表明，该算法在结构化道路的静态避障环境中规划出的路径平稳、曲率更小、运行时间快，相比较传统的Apollo算法更平稳可靠。

　　关键词：路径规划；二次规划；智能网联汽车

　　0引言

　　自动驾驶可能通过人工智能和计算机硬件的进步来改变交通运输[1]。路径规划[2]是自动驾驶汽车运动规划的关键组成部分，对车辆的安全性、舒适性至关重要[3]。目前，对于路径规划，算法通常被分为两类：基于优化的路径规划算法和端到端的路径规划算法。端到端的规划方法[4]也称为基于学习的方法，将原始的传感器数据直接映射到轨迹点或控制信号。基于学习的规划方法有通过评估状态和动作之间最大的适应性映射，使智能体尽可能达到专家轨迹的模仿学习[5]；通过不断与环境交互过程中试错获得最大累积奖励，逐渐获得最优策略以达到目标的强化学习[6]等。该方法不会出现人为定义的信息瓶颈，从而有更好的场景泛化能力[7]。然而，端到端面临一个关键的可解释性问题。没有中间输出，难以跟踪错误的初始原因并解释为什么模型到达特定的控制命令或轨迹变得更困难[8]。

　　基于优化的方法是比较灵活的方法，通过解决最优控制问题来完成，在满足多种类型的硬约束或者软约束的情况下最小化预定义的代价函数[9]。在全局坐标系中运用二次规划，直接计算轨迹(同时计算路径和速度)[10]。将轨迹在全局坐标系中离散化，并将这些离散化的状态作为优化变量。优化过程不断迭代，找到一个最小化目标函数的轨迹，该目标函数结合了安全性和舒适性[11]。优化方法的优点是它们提供了最优性建模的直接执行。

　　此外，由于路径/轨迹被密集离散化作为优化变量，这些方法实现了对路径/轨迹的最大控制，以处理复杂场景[12]。除了在全局坐标系内进行路径/轨迹规划的方法外，还有一些方法将规划问题转化到不同的空间，以降低规划的复杂性。在文献[13]中，轨迹规划是在Frenet坐标系中进行的，该坐标系由一条光滑的参考线组成。车辆的运动被解耦为2个一维运动，关于参考线的纵向运动和横向运动。Frenet坐标系规划的优点是有效地利用道路结构以实现更清晰的场景理解，其中包括行驶道路边界[14]和各种类型的车道线[15]。

　　针对结构化道路路径规划问题，本文提出一种基于优化的规划方法。该规划方法可以使无人车得到安全无碰撞且曲率变化小的路径。对于避让障碍物的路径规划问题是非凸问题，难以直接用最优化方法求解的难题[16]。将全局导航的路径进行截取、平滑处理，以建立Frenet坐标系。再将规划空间离散化，用动态规划（Dynamic Pro-gramming，DP）在离散空间中分割出避让静态障碍物的凸空间。在凸空间中用二次规划（Quadratic Programming，QP）优化出一条最优的路径。在Prescan、Carsim和Mat-lab/Simulink联合仿真平台对所提算法进行验证，通过设计结构化道路上的静态障碍物验证算法的有效性和优越性。

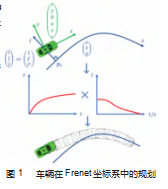
　　1参考线平滑

　　在Frenet坐标系中进行路径规划，如图1所示。将全局坐标系中车辆的状态在Frenet坐标系中描述，进行路径规划，它由一条假定的参考线（reference line）定义。在结构化道路中，对于车辆的运动规划，平滑的参考线可以是导航路径，即道路中心线[17]。

　　一条参考线是在Frenet坐标系中规划的前提。通常，参考线表示为全局坐标序列，即1 x 1,y1,P x2,y2,…,Pn(xn,yn)。由于参考线作为地图和Frenet坐标系的桥梁，它的平滑性极大地影响了规划路径的质量。根据全局坐标系—Frenet坐标系的转化[18]，为了精确地将路径映射到曲率级，参考线必须是一阶导数连续的，即参考线的曲率导数是连续性的。

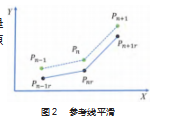
　　在参考线几何信息确定的情况下，提出一个基于二次规划的平滑算法。

　　|Pnr Pn−1r+Pnr Pn+1r|衡量平滑性，|Pn Pnr|衡量与原路径点的相似性，|Pn−1rPnr|+Pnr P(n+1r)衡量路径点间的均匀性，如图2所示。

　　设原路径点坐标X=(x1,y1,x2,y2,…)T，平滑后的路径点坐标Xref=(x1r,y1r,x2r,y2r,…)。

　　问题描述为原导航路径点坐标P 1(x1,y1),P2(x2,y2),…,Pn(xn,yn)已知，求P 1r(x1r,y1r),P2r(x2r,y2r),…,P nr(x nr,y nr)，使得上面3个衡量标准最小，并且满足约束|X−Xref|≤buff。将路径点的坐标代入优化目标构建代价函数，用二次规划求解器解出优化变量（平滑后参考线的坐标位置）Xref=(x1r,y1r,x2r,y2r,…)T。

　　2基于离散S-L空间的路径规划

　　2.1路径动态规划算法

　　在Frenet坐标系中给定一条平滑的参考线，沿着与参考线相切方向为S轴，正交于参考线方向为L轴，将规划空间转化为SL空间。车辆在全局坐标系中的运动被解耦为2个独立的一维运动，纵向运动沿着S轴，横向运动沿着L轴。由于无人车对静态障碍物进行避障的可行驶区域为非凸空间如图3所示，该规划问题为非凸优化问题，难以通过优化方法求最优解[19]。而动态规划可以在离散的规划空间中给出一个粗略解，从非凸空间中分割出凸空间，将问题转化为凸优化问题，进而可以用二次规划求解器求最优解[20]。

　　根据所需路径规划长度确定纵向采样间隔，根据障碍物的大小确定横向采样间隔，从而获得待规划的离散SL空间。无人车路径动态规划问题可以描述为在离散SL空间中根据设定的代价函数，从起点开始逐步搜索代价最低的路径点直到终点，再从后向前遍历得到规划路径，如图4所示。其中连接各个路径点的曲线是根据初末状态约束求得的最优曲线，如图5所示。

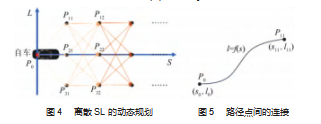
　　路径点之间的连接曲线l=f(s)需要满足舒适性要求和边界的状态约束。舒适性的评价指标为Jerk=，其中a为加速度。以连接采样点P0和P 11为例，始末点的约束为：

　　Jerk=取极小值的解函数[7]。f'(s)=df(s)/ds表示对弧长的导数，是一种几何关系。在确定采样点之间的连接曲线后，根据代价函数计算每段路径的代价。根据对SL空间离散采样的密度不同，需要再在每段路径上以Δs为间距插值以更精确计算路径的代价。设障碍物obs的坐标为(s,l)如图6所示。

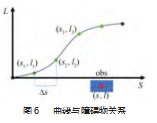
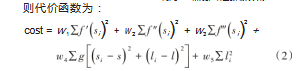
　　式中：l为与参考线的距离；f'、f″、f‴为分别l对s的各阶导数；g为路径点距离障碍物的距离函数，可用式（3）表示；w 1、w2、w3分别为各阶导数的代价权重；w4为与障碍物重；考线距离的代价权重。

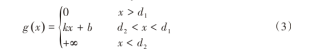
　　以此计算出每相邻两列间每两个路径点的代价，从而可以根据式（4）计算出从起点到最后一列每个点的最小代价，再从中选择最小的将其经过的路径点作为动态规划输出。cost(P0,Pij)表示从起点P0到终点Pij的最小代价。

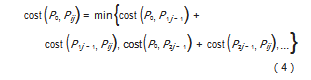
　　2.2路径二次规划算法

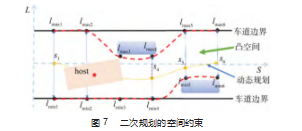
　　根据动态规划的结果从有障碍物的非凸空间分割出凸空间，可以利用二次规划的方法对凸优化问题求解出最优解，从而获得路径规划的最终路径。二次规划的约束为将车辆约束在红色虚线的凸空间内，如图7所示。

　　动态规划在车道边界内规划出离散最优路径（黄色路径）将障碍物分割出去，开辟出凸空间（红色曲线内）。当路径的s=si时自车的轮廓应该在lmini~lmaxi之间（i=1,2,3,…）如图7所示。用矩形将自车（host）简化并约束凸空间内。设自车质心纵坐标为si，d 1为质心到前部的距离，d2为质心到后部的距离，4个角点的横坐标分别为lP1、lP2、lP3、lP4，记ubi为(si−d2,si+d 1)中lmaxi的最小值，记lbi为(si−d2,si+d 1)中lmini的最大值，则碰撞约束为：

　　对参考线即SL坐标系的坐标轴，离散化取等距Δs为采样点，通过分段加加速度优化法求解自车质心si对应的li。假设连接si与si+1的曲线l=f(s)的三阶导数恒为为了路径连续，点i和点i+1之间还有额外的等式约束（二阶连续性约束）：

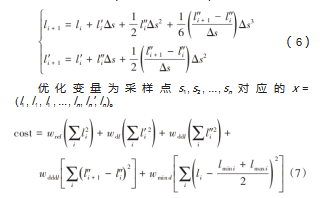
　　式中：wref为与参考线的距离代价权重；wdl、w ddl、wdddl分别表示l对s的一阶、二阶、三阶导数代价权重；wmind为与凸空间中央距离代价权重。

　　整个二次规划的代价函数由式（7）表示，约束有式（5）和式（6）。求解出l1,l,l,…,ln,ln',l与s1,s2,…,sn相结合，得到二次规划下的最优路径。

　　3仿真结果及分析
       3.1仿真平台

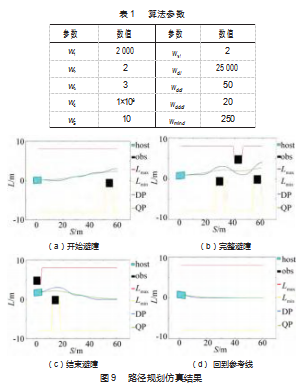
　　仿真软件有Carsim2020.0、MATLAB2020a、Pres-can8.5。其中，Carsim可以获得车辆的动力学模型；Pres-can用于设置仿真场景、获取车辆位置、感知障碍物信息等；MATLAB处理搭建整体的算法框架、处理定位、障碍物、车辆动力学信息，用于具体的决策规划和控制实现。

　　3.2静态避障实验

　　本文以Prescan作为仿真环境，创建自车、障碍车、道路并为自车配备理想传感器等搭建仿真环境，通过设置障碍车的位置和状态建立实验环境如图8所示。传感器固定在自车的前部，采集障碍车的位置，全局导航为沿着右侧车道中心行驶。算法中各个代价权重参数如表1所示，设置多辆道路上的静态障碍车，自车从开始感知到障碍车规划避障路径到驶过障碍区域规划回到参考线路径的过程如图9所示。图9（a）中自车感知到障碍物时，动态规划会规划出一条距离障碍物较远的路径，如图中蓝色曲线所示，黑色矩形为障碍车辆。图9（b）中蓝色曲线是动态规划根据离散采样点的位置和障碍物与参考线的距离决定的绕行方式，由此决定了自车可行驶区域的左右边界为图中红线和黄线。可以看出，动态规划在存在障碍物的非凸空间中对每个障碍物做决策，将障碍车辆从行驶区域中分割出去。图9（c）中当路径驶过障碍车时DP规划回到参考线的路径，使车辆沿着车道中心线行驶。图9（d）中当没有障碍物时，动态规划和二次规划的最优路径一致，均与参考线重合。从整个图9描述的过程可以看出，动态规划的路径比较保守，曲率较大。二次规划在凸空间中优化出一条比动态规划更平滑、曲率更小且靠近参考线的路径。

　　4结束语

　　本文针对自动驾驶车辆路径规划问题，提出了基于二次规划的路径规划方法，可以使车辆平稳、安全、高效地行驶。搭建了Prescan、Carsim和MATLAB联合仿真平台，设计了避让静态障碍物的实验。仿真实验结果表明，本文提出的路径规划方法具有路径平滑、曲率小的优点。

　　参考文献：

　　[1]CHEN L,TENG S Y,LI B,et al.Milestones in autonomous driv- ing and intelligent vehicles—part II:perception and planning[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2023,53(10):6401-6415.

　　[2]ZHANG J L,WANG Z Y,CHEN C.A hierarchical path planning method based on key points generation[C]//2023 IEEE Interna-tional Conference on Smart Internet of Things(SmartIoT).Xini-ng:IEEE,2023:23-29.

　　[3]YURTSEVER E,LAMBERT J,CARBALLO A,et al.A survey of autonomous driving:Common practices and emerging technolo-gies[J].IEEE Access,2020,8:58443-58469.

　　[4]MUHAMMAD K,ULLAH A,LLORET J,et al.Deep learning for safe autonomous driving:current challenges and future directions[J].IEEE Transactions on Intelligent Transportation Systems,2021,22(7):4316-4336.

　　[5]ZHANG Z M,TIAN R R,SHERONY R,et al.Attention-based in-terrelation modeling for explainable automated driving[J].IEEE Transactions on Intelligent Vehicles,2023,8(2):1564-1573.

　　[6]YUE L J,FAN H M.Dynamic scheduling and path planning of au-tomated guided vehicles in automatic container terminal[J].IEEE/CAA Journal of Automatica Sinica,2022,9(11):2005-2019.

　　[7]BEN ELALLID B,BENAMAR N,HAFID A S,et al.A compre-hensive survey on the application of deep and reinforcement learning approaches in autonomous driving[J].Journal of King Saud University-Computer and Information Sciences,2022,34(9):7366-7390.

　　[8]ZHU B,JIA S Z,ZHAO J,et al.Review of Research on Decision-making and Planning for Automated Vehicles[J].China Journal of Highway and Transport,2024,(1):215-240.

　　[9]GAO F,WU W,PAN J,et al.Optimal time allocation for quadro-tor trajectory generation[C]//2018 IEEE/RSJ International Con-ference on Intelligent Robots and Systems(IROS).Madrid:IEEE,2018:4715-4722.

　　[10]ZIEGLER J,BENDER P,SCHREIBER M,et al.Making bertha drive—an autonomous journey on a historic route[J].IEEE Intel-ligent Transportation Systems Magazine,2014,6(2):8-20.

　　[11]GUO Y Q,YAO D Y,LI B,et al.Down-sized initialization for optimization-based unstructured trajectory planning by only op-timizing critical variables[J].IEEE Transactions on Intelligent Vehicles,2023,8(1):709-720.

　　[12]宋春雷,张嘉轩,田晓春,等.基于优化的离散空间轨迹规划算法[J].中国惯性技术学报,2023,31(11):1150-1156.

　　[13]WERLING M,ZIEGLER J,KAMMEL S,et al.Optimal trajecto-ry generation for dynamic street scenarios in a Frenét frame[C]//2010 IEEE International Conference on Robotics and Automa-tion.Anchorage:IEEE,2010:987-993.

　　[14]魏荣琨,马荣,赵龙庆,等.基于激光雷达梯度滤波的道路边界检测[J].机电工程技术,2023,52(12):207-212.

　　[15]徐嘉雯,何超,魏明洋,等.基于特征提取的车道线快速检测方法研究[J].机电工程技术,2023,52(2):118-122.

　　[16]李柏.复杂约束下自动驾驶车辆运动规划的计算最优控制方法研究[D].杭州:浙江大学,2018.

　　[17]EIRAS F,HAWASLY M,ALBRECHT S V,et al.A two-stage optimization-based motion planner for safe urban driving[J].IEEE Transactions on Robotics,2022,38(2):822-834.

　　[18]TOPONOGOV V A.Differential geometry of curves and surfac-es:a concise guide[M].Boston:Birkhäuser,2006.

　　[19]MALYUTA D,REYNOLDS T P,SZMUK M,et al.Convex opti-mization for trajectory generation[EB/OL].arXiv:2106.09125.http://arxiv.org/abs/2106.09125,2021.

　　[20]Fan H,Zhu F,Liu C,et al.Baidu apollo em motion planner[J].arXiv preprint arXiv,2018:1807.08048.