摘要：为了提高新能源商用车的续航能力，对其后背式电池框架进行轻量化设计。使用NSGA-Ⅱ算法进行优化设计，建立优化模型并验证其力学性能，选择优化设计变量，采用最佳空间填充设计（OSF）进行实验设计获得初始样本点，并选取验证点与建立的克里金（Kriging）模型进行拟合分析，判断Kriging模型的准确性且进行响应面优化，通过NSGA-Ⅱ算法建立优化模型，寻找最优的解集，完成对电池框架的轻量化设计，并对优化结果进行验证分析得出：电池框架在极限工况且满足强度的情况下最大应力增加了4.72%，质量减少了8.6%，达到了轻量化设计的目标。

　　关键词：电池框架；最佳空间填充设计；Kriging模型；NSGA-Ⅱ;轻量化设计

　　0引言

　　随着科技的快速发展，能源短缺与环境污染问题日益突出。汽车作为交通运输的主要工具，其保有率约11%的商用车却需要消耗51%的汽柴油，并且制造了56%的碳排放量[1]，所以新能源商用车的研发能够很好解决能源和环境的问题。本文将通过对电池框架的轻量化设计来达到增加新能源商用车续航里程的目的。

　　宋兴华等[2]通过Workbench对储能仓电池架进行了仿真分析来判断电池架设计的可行性。王登峰等[3]使用Isight建立多目标优化模型来目标进行优化设计，通过软件计算来协调多个参数之间复杂的关系，使设计更加合理；Dammak Khalil等[4]使用Kriging模型来对汽车的刹车片进行优化设计并取得较为理想的优化结果；曾漾等[5]人通过将响应面模型与遗传算法相结合，对钢制舱壁的结构进行优化设计，最终优化结果在满足条件的情况下减重23%；Kriging模型作为响应面模型的一种，是估计方差最小的估计模型，包括非参数和多项式回归两部分，并且需要的样本点较少，在解决非线性程度较高的问题时也能取得比较理想的拟合效果[6]。

　　本文对矿区所使用的新能源自卸车的电池框架进行轻量化设计，通过Workbench软件来进行静力分析来判断优化设计的可行性，静力分析的结果通过响应面法来进行优化设计，避免了优化设计过程每次迭代需要重新设计参数化模型的复杂操作，对于生成的结果使用NSGA-Ⅱ算法进行全局搜索进而得到Pareto最优解。

　　1电池框架的有限元分析

　　设计好的三维数模在进行有限元分析之前先对其进行简化处理，便于降低模型的前处理工作量。简化后的模型在Workbench中进行前处理工作：划分网格大小为17 mm的网格，节点总数为1 139 916，单元总数为246 978，材料选取Q235。其材料参数如表1所示。

矿区用车所需要面对的道路情况较为复杂，会使整车产生颠簸、急刹、转弯等工况，而其产生的惯性力对整车零部件的强度要求很高。通过分析得到对于电池框架产生较大载荷的极限工况下的载荷加速度情况见表2[10]

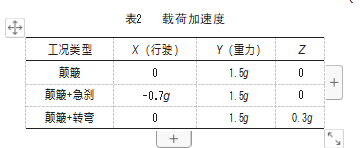
　　其中g=9.8 m/s2。根据牛顿第二定律：

　　F=ma得到颠簸工况和急刹工况下各部件所受到的载荷力情况，在Workbench中施加受力情况进行静力分析。

　　对其中较为极限的两种工况：颠簸加急刹和颠簸加转弯进行静力分析，通过Workbench静力分析得出复杂工况下的等效应力，如图2~3所示。颠簸加急刹的最大等效应力为145.57 MPa、颠簸加转弯的最大等效应力为71.87 MPa。这两种极限工况中颠簸加急刹的等效应力更大，此时安全系数为1.6，还有较大优化空间，后续优化将根据此工况进行优化设计。

      2优化设计

　　2.1数学模型的建立

　　在Solidworks中对电池框架的零件厚度进行参数化设计，根据其结构特点得到6个设计变量分别为：立柱、底部纵梁、冷却机组支撑杆、纵梁、斜梁拉杆和电池支撑杆的厚度，将其设置为设计变量Xi=[x 1,x2,x3,x4,x5,x6]T，设计变量的上下值设定可表示为：

　　xiL≤xi≤xiU（2）

　　式中：xi为设计变量X中的各元素；xiL为设计变量的下限值；xiU为设计变量的上限值。

　　以总质量m(x)最小和等效应力σ(x)最小为优化目标，同时电池框架的刚强度在极限工况下满足要求，以此为xi≤xiU（3）

　　式中：[σ]为材料的许用应力，MPa。
      2.2响应面分析

　　实验设计模块（DOE），根据设计变量的取值范围，采用最佳空间填充设计（OSF）进行实验设计，可更好地适配Kriging模型[12]，以此来构建一个准确的响应面模型。

　　Kriging模型是响应面法的一种形式，该方法具有统计学特征[13]：式中：fi(x)为回归模型，fi(x)={f1(X),f2(X),⋯,fp(X)}；βi为相关参数，βi={β1,β2,⋯,βn};Z(x)为均值为0的统计分布，用协方差表示其相关程度；σ2为方差；y为近似值；n为设计变量的数量；R(x,x.)为基于设计点相对位置的相关函数；θj≥0；0≤Pj≤2，取Pj恒等于2。

　　建立Kriging模型的数学模型为[14]:（5）　=(FTR-1 F)-1 FTR-1 Y

　　式中：为预测点的近似值；R为相关性矩阵；r为相关

　　矢量，rT=[R(x 1,x),R(x2,x)⋯,R(xn,x)]；Y为设计点的目标值；F为设计点的基函数矩阵；为β的广义最小平方估计量。

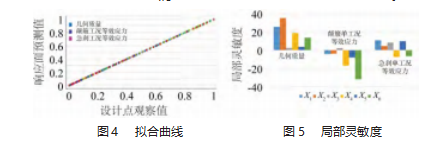
　　响应面分析之后得到各设计点的离散图，采用Krig-ing模型优化时必须设置验证点，其数量为3个。拟合的评判标准是：越靠近y=x直线表明拟合度越高，也意味着拟合越好[15]。通过拟合曲线中对响应面预测值和设计点观察值的拟合度可以验证克里金模型与NSGA-Ⅱ算法联合进行优化设计的准确性，如图4所示。同时通过响应面分析得出的局部灵敏度可以反映处输入输出变量的关系[16]，可以看出对于几何质量，6个设计变量都与之成正相关，而对于两个单工况根据实际受力部分设计变量与之成负相关，即部分设计变量相关的几何质量和等效应力相互矛盾，如图5所示。因此，通过多目标遗传算法可以在保证轻量化的情况下同时得到等效应力的最小解。

       2.3 NSGA-Ⅱ算法

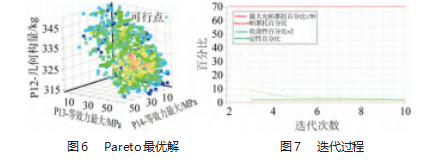
　　建立Kriging模型后，这些模型可视为目标函数。在此基础上，应用NSGA-Ⅱ算法搜索Pareto最优解。NS-GA-Ⅱ算法是一种混合变种算法，它支持各种类型的输入函数，并且遗传作用于整个种群，同时又强调个体的整合，是解决多目标问题的有效办法[17]。设置初始种群6 000个，交叉概率为0.9，每次迭代1 200个样本迭代20次，样本点的总数为2.88×104个。根据优化过程设置的响应面边界条件，经过多次迭代得到如图pareto最优解，如图6所示。图中方块的颜色表示优化结果的优劣，蓝色为最优解，红色代表最劣解。

　　电池框架各参数具体优化迭代过程如图7所示，迭代到16 455次开始收敛。迭代过程中等效应力始终贴近给的许用应力值，而几何质量在第一次迭代过程中变化幅度特别大，后面伴随着每一次迭代都在逐步减小，最后趋于平稳。

     3优化设计结果验证

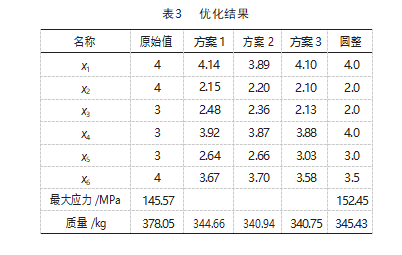
　　根据NSGA-Ⅱ算法不断迭代搜索，最终得到3个候选点，即3个方案。对3个方案进行比对发现方案1的优化效果不够明显，对方案3进行圆整，具体参数如表3所示。
      3.1模态分析验证

　　电动商用车在实际道路行驶时，电池框架受到的主要激励源为因路面不平产生的载荷和电机的振动载荷，而优化过程中要避免电池框架与激励源产生共振，影响电池框架的寿命[18]。激励频率f可以通过式（6）计算：

　　式中：S为轮胎的周长；v为行驶速度；rd为轮胎的滚动半径。

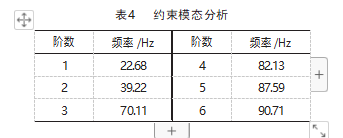
　　考虑行驶工况，矿区用车根据国家规定设置的速度应该低于90 km/h，车轮轮胎型号为12.00R20，由此可以得出滚动半径为0.546 m，将值代入式（4）得f=7.29 Hz，通常实际模态频率应该和激励频率错开2 Hz以上[15]。对优化前的模型进行约束模态分析得到表4的结果，通过比对可以看出电池框架并不会与激励源产生共振，也就意味着优化的合理性。

      3.2静力分析验证

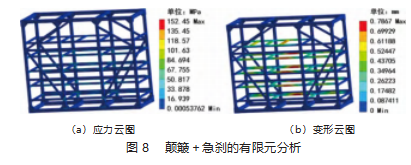
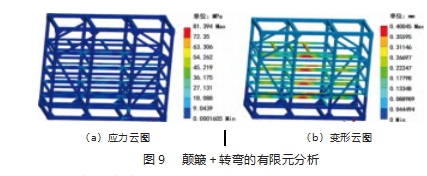
　　将优化方案圆整后，得到各设计变量的数值，对三维模型的截面尺寸进行调整，然后进行静力分析。可以看出，根据颠簸加急刹这一极限工况进行优化设计得到的三维模型在刚强度上可以达到要求，此时电池框架的最大应力增加了4.72%，安全系数为1.54，质量减少了8.6%，最大变形也由1.76 mm变为0.78 mm，降低了55.68%。完成了对电池框架的轻量化设计。在颠簸加转弯工况下的依旧可以满足要求。圆整后的数据进行验证分析得到的应力云图和变形云图如图8~9所示。

      3.3实际生产验证

　　根据有限元分析结果所得出的方案3进行实际生产验证，如图10所示，实际生产的电池框架安装于试制的新能源自卸车上前往相关部门上公告，以验证试制的可行性，通过车辆检测机构验证，符合安全标准，也意味着优化结果的可靠性。

　　4结束语

　　（1）本文对矿区所使用的新能源自卸车的电池框架进行优化设计，将MOGA算法改为NSGA-Ⅱ算法与Krig-ing模型结合进行响应面优化，达到更好的优化效果。

　　（2）本文提出的优化设计方法对电池框架进行优化设计，使得电池框架的整体重量减少了8.6%，优化效果明显。

　　（3）本文的优化并不是限于仿真的理论层面的优化，也根据优化结果进行生产验证，具有一定的实用价值。

      参考文献：

　　[1]齐羿,于海淼,冯启飞,等.新能源商用车发展趋势和应对策略[J].重型汽车,2023,194(2):38-39.

　　[2]宋兴华,殷帅兵,王哲,等.基于ANSYS Workbench的电池架仿真分析[J].科技视界,2019,285(27):58-60.

　　[3]王登峰,张帅,陈辉,等.基于疲劳试验的车轮拓扑优化和多目标优化[J].汽车工程,2017,39(12):1351-1361,1374.

　　[4]Dammak Khalil,Baklouti Ahmad,El HamiAbdelkhalak.Optimal reliable design of brake disk using a Kriging surrogate model[J].Mechanics of Advanced Materials and Structures,2022,29(28):7569-7578.

　　[5]曾漾,周俊,沈志远,等.基于响应面法的复合材料舱壁结构优化设计[J].重庆大学学报,2020,43(6):82-89.

　　[6]万云发,孙文磊,王宏伟,等.基于Kriging模型与MOGA算法的风力机主轴轻量化设计[J].太阳能学报,2022,43(3):388-395.

　　[7]翟玮昊,龚敏浩,林名润,等.基于主动学习的Kriging模型的可靠性分析[J].空天防御,2023,6(1):1-5.

　　[8]李家辉,许锋.基于Kriging模型与MOGA算法的有限元模型修正[J/OL].航空工程进展:1-8[2023-06-06].

　　[9]刘永良,刘爽,程荫,等.基于Kriging修正模型的贴片机横梁优化设计[J].现代机械,2023(2):31-35.

　　[10]孙丰科.55 t汽车起重机车架结构多工况优化设计[D].大连:大连理工大学,2022.

　　[11]何山,齐凯,江爱华,等.遗传算法在门式起重机轻量化设计中的应用[J].起重运输机械,2016(3):1-3.

　　[12]Mckaym D,Beckman Rj,Conover Wj.Comparison of three meth-ods for selecting values of input variables in the analysis of out-put from a computer code[J].Technometrics,1979,21(2):239-245.

　　[13]马静静,殷红,彭珍瑞,等.基于Kriging模型的损伤识别方法[J].机械强度,2020,42(4):786-792.

　　[14]Ankenman B E,Nelson B L,Staum J.Stochasti Kriging or Simu-lation Metamodeling[J].Operations Research,2010,58(2):371-382.

　　[15]Peng Xingyu,Xu Ling,Gao Jian.Reliability analysis of city gas pipelines subjected to surface loads based on the Kriging model[J].Proceedings of the Institution of Mechanical Engineers,Part O:Journal of Risk and Reliability,2023,237(1):69-79.

　　[16]Wang P,Wu G Q.Multidisciplinary design optimization of vehicle instrument panel based on multi-objective genetic algorithm[J].Chinese journal of mechanical engineering,2013,26(2):304-312.

　　[17]韦永平,盛遥,曾桃涛,等.商用车蓄电池箱体频率响应分析及结构改进[J].西南汽车信息,2018.

　　[18]Yu Feng,Xie Jun.Modal analysis and improvement of the frame for all-terrain vehicle[J].Noise&Vibration Worldwide,2018,49(11).