摘要：丝杠进给系统在运行过程中具有非线性、强耦合和参数时变等特点，由于传统PID控制器的参数固定，无法很好地适应系统变化，从而导致系统响应速度缓慢及跟踪性能较差。针对此类问题，将复杂的丝杠进给系统简化处理并建立二质量系统模型；对传统的模糊规则加以优化和改进，设计了一种模糊PI控制与加速度前馈补偿相结合的复合控制器。模糊PI控制器根据实际系统特性调整模糊规则，使得控制器参数自适应变化，提高控制效果；加速度前馈补偿控制器根据输入信号预先补偿系统，提升了系统带宽。在Simulink中搭建系统模型，在阶跃输入和干扰输入下对比观察2种控制器作用的系统响应曲线。经仿真验证，丝杠进给系统的动态特性、稳态特性和抗干扰能力都得到了明显地提升。

　　关键词：丝杠进给系统；模糊PI控制；前馈补偿；动态特性

　　0引言

　　滚珠丝杠具有结构简单、摩擦小、精度高等优点，使其在工业机器人第七轴、数控机床等工业化设备上得到广泛应用。丝杠进给系统由驱动器、永磁同步电机、联轴器、滚珠丝杠、导轨、工作台、轴承等组成，它是一个多耦合、参数时变、存在柔性连接的非线性系统，它的动力学模型异常复杂，这将增加控制器的设计难度。

　　丝杠进给系统一般采用传统的PID控制，该方法适用面广，并且原理简单便于调试，但是考虑到进给系统是个参数时变的非线性系统，PID控制器并不能完全适用各种工况。尤其是在进给系统运行的起始阶段，由于存在负载自重和惯性等因素，控制器参数无法自适应调节，使得转速响应滞后且跟踪偏差较大。针对传统PID控制的缺陷，众多学者也对此展开研究。陈鹏展等[1]基于曲线拟合和最优控制理论，提出一种速度环参数自整定方法。李文庆等[2]利用最小二乘法对伺服进给系统进行参数辨识，将辨识出来的参数输入系统计算得出控制器的各项参数。Yu J P等[3]设计了一套自适应神经网络的驱动系统，经实验证明，即使系统存在未知干扰，仍旧拥有良好的跟踪特性。Errouissi R和Noriega G等[4]充分考虑了被控系统的非线性特点，采用预测控制策略，使其应用至进给系统中，增加了它的稳定性和快速性。随着高级智能算法的不断发展，将先进的智能算法和传统控制算法相结合已经是一种新的研究趋势。模糊控制作为新型智能算法，其具备较强的鲁棒性，适用于那些难以建立精确数学模型的复杂对象，并且可以与传统PID控制相结合。

　　然而此类控制器是以误差信号作为输入，一定程度上会造成系统延时，因此在保证系统稳定的情况下，为尽可能提升系统响应速度，缩减系统的速度信号跟随误差，可以使用前馈补偿器预先补偿信号变化对被控对象的影响[5]。本文详尽分析丝杠进给系统的动态特性，建立其数学模型，并将模糊PI控制与加速度前馈补偿相结合，设计一个复合控制器，在Simulink中搭建系统模型，和传统PID控制器的仿真结果对比，从而验证所设计的复合控制器的有效性和先进性。

　　1丝杠进给系统动力学建模

　　丝杠进给系统包括伺服驱动系统、检测装置、永磁同步电机、机械传动系统以及负载，其主要是由电子驱动装置和机械传动装置组成[6-7]。由于存在柔性负载，且滚珠丝杠刚度有限，整个伺服进给系统是一个多惯量的复杂系统，对其建模和分析都十分困难。故对该模型简化处理，得到一个二质量系统模型[8]，如图1所示。

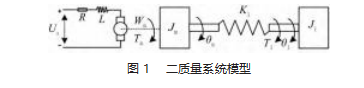
二质量系统由驱动部分、传动部分和负载部分组成。根据各部分的工作原理，建立以下方程。

　　式中：i为定子电流；R为定子绕组电阻；s为拉氏变换中的复变量；Jm为电机转动惯量；Jl等效为丝杠和负载转动惯量；θm和θl分别为电机与负载的转角；bm和Jl分别为电机与负载的阻尼系数；Kb为反向电动势常数；Kl为丝杠刚度系数；Km为电流放大倍数；Tm为电机转矩；Tl为负载转矩。

　　丝杠进给系统具备复杂的机电耦合特性，根据各部分的运动原理和平衡方程，建立对应的动力学方程，如式（1）~（4）所示。为了简化计算，将此类方程由时域转换至复数域，推导其输入输出关系并分析系统特性，最后根据推导出的传递函数，在Simulink中完成丝杠进给系统模型的搭建。

　　2速度环模糊控制器设计
      2.1模糊控制器原理

　　模糊控制器的设计以模糊数学、模糊语言形式的知识表示以及模糊逻辑的规则和推理为基础，通过检测被控系统的反馈信号，计算给定值r（t）和反馈值y（t）之间的偏差e（t）及其变化率ec（t），并对它们模糊化处理，将精准的输入信号转换为该论域中的模糊子集，即模糊输入；再根据模糊逻辑规则将模糊输入E和EC映射至相应的规则库单元，采用模糊数学理论对相应的规则库单元推理计算，得到一个输出模糊集合或输出隶属函数，最后对其进行去模糊化处理，得到准确的输出ΔKp和ΔKi[9]，其工作原理如图2所示。

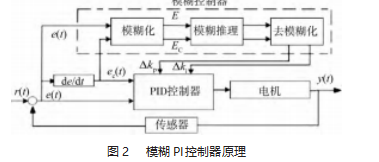
      2.2确定各变量隶属度函数及论域

　　考虑到速度环的好坏将直接影响伺服进给系统的动态特性，故对其采用模糊PI控制，电流环则继续沿用传统的PI控制[10]。模糊控制的输入量e（t）、ec（t）以及输出量ΔKp、ΔKi的模糊子集都设置为{NB，NM，NS，ZO，PS，PM，PB}，分别代表负大，负中，负小，零，正小，正中，正大；论域为[-3，3]，则其量化等级为{-3，-2，-1，0，1，2，3}。

　　隶属度函数是将模糊子集映射至单位实数区间[0，1]的函数，MATLAB的模糊工具箱集成了双S型、高斯型、三角形等11种隶属度函数[11]。为了便于计算，一般将模糊输入和输出的隶属度函数都设置为三角形，通过调整a、b、c共3个参数，完成隶属函数的设计。其数学表达式如下，形状如图3所示。

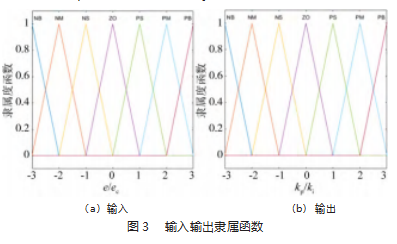
      2.3设计模糊控制规则

　　模糊PI控制器的核心就是模糊规则库，模糊规则设定的好坏将直接影响控制器参数，最终影响整个系统。因此，根据控制器参数对系统的影响，归纳总结被控系统在运行过程中对于不同偏差和偏差变化率的响应结果，对传统的模糊规则加以改进，设计如下参数自整定的规则[12]。

　　当偏差绝对值偏大时，需要立即加快响应速度，因此便增大比例系数，期间为避免积分饱和，防止出现较大的超调量，便不采用积分环节；当偏差绝对值中等时，为避免出现超调情况，需要减少输出量，故减小比例系数，同时利用积分环节消除静态偏差，需要增大积分系数[13]；当偏差绝对值偏小时，需要尽可能消除系统的稳态偏差并提高系统的抗干扰能力，因此需要设置较大的比例系数和积分系数。

　　当偏差变化率较大时，既要缩减调节时间又要防止超调，则选择中等比例系数和较小的积分系数；当偏差变化率中等时，需要进一步增加比例系数和较小的积分系数，以保持系统的稳态特性；当偏差变化率较小时，为提升响应时间，需要选择偏大的比例系数和较小的积分系数。

　　根据上述详尽的分析和说明，制定相应的模糊控制规则如表1所示。

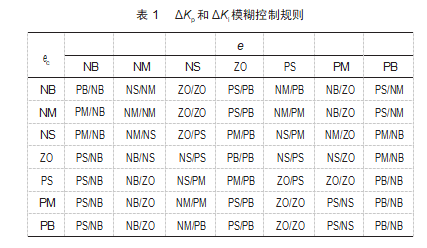
      3前馈补偿控制器设计

　　在丝杠进给系统中，多数控制器是以系统给定值和反馈值的误差e（t）作为输入，通过修正误差来达到控制目的。由于此类控制方法是根据被控对象的反馈信息进行工作，势必出现响应时间较慢的情况。前馈补偿控制器是在系统工作之前，预先补偿信号变化对被控对象的影响，并且和反馈环节联合形成闭环回路。前馈补偿控制器有效地提高了系统的响应速度，减少了稳态误差，提升了跟踪精度。前馈补偿控制结构如图4所示。

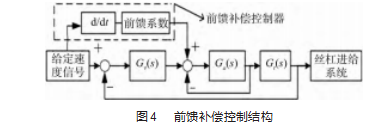
       式中：Gv(s)为速度环传递函数；Ga(s)为等效电流环传递函数；Gt(s)为伺服电机传递函数；Fa(s)为加速度前馈传递函数；τa和Ka分别为电流环时间常数和惯性环节增益；Kv和τv分别为转速环控制器参数。

　　根据系统传递函数为1，可以求出加速度前馈传递函数：为了方便计算，对上述系统模型简化处理，其中电流环时间常数较小，可以等效为0，因此前馈系数为

　
　系统拥有前馈补偿控制器，则无需等待误差信号

　　再进行反馈控制，将二者结合，可以减少稳态误差及提升系统的反馈速度[14]。

　　4系统仿真分析

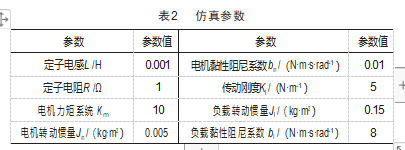
　　根据丝杠进给系统的动力学模型，在Simulink中搭建相应的框架；依据模糊控制原理和模糊控制规则，在MATLAB的模糊工具箱中完成相应模糊控制器的设计，应用至速度环，并和加速度前馈补偿控制器相结合，而电流环则依旧使用常规的PID控制。仿真参数如表2所示。

     4.1阶跃输入下系统仿真
      设置总的仿真时间为20 s，整个系统的输入信号是幅值为1 000的阶跃信号。通过仿真得到系统在复合控制器作用下的各种响应曲线，并和传统的PID输出曲线进行对比和分析结果如图5所示。

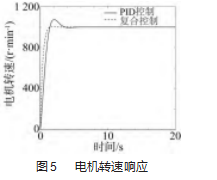
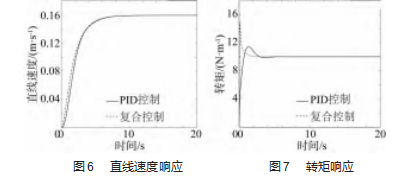
　　直线速度响应如图6所示。由图可知，在复合控制器控制下，电机在1.4 s就达到设定转速1 000 r/min，整个运行过程几乎没有超调出现，而PID控制下的系统在4.3 s达到稳态，且产生的7.7%超调量。从工作台的直线速度响应曲线来看，复合控制器下的系统动态特性更佳；但由于存在柔性连接，工作台动态响应速度略慢于电机。

　　电磁转矩响应曲线如图7所示。由图可知，在起始阶段复合控制器作用下的电机转矩快速达到最大值15 N·m，然后逐渐降低达到稳态转矩10 N·m。而常规PID控制下电机扭矩起始阶段只有11.7 N·m，上升时间为0.8 s。复合控制器作用下系统时间明显缩短，且初始扭矩较大，利于设备工作。

       4.2施加干扰后系统仿真

　　为了验证控制器的抗干扰能力，第9 s时，分别在模型中添加一个幅值为40的脉冲干扰信号，该信号由2个阶跃信号相减得到。在此干扰信号的作用下，对比观察各个响应曲线，结果如图8～10所示。

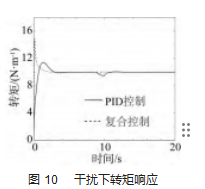
根据电机转速响应曲线和转矩响应曲线可以看出，复合控制器在干扰信号的作用下产生的幅值明显小于PID控制器，并且可以快速返回稳定状态，前者结合系统工况的变化，对自身参数迅速调整，促使跟踪偏差迅速降为0。由干扰下工作台直线速度响应曲线发现曲线总体变化趋势大致相同，但是复合控制器下的速度响应几乎没有波动，从而一再证明其鲁棒性能好，抗干扰能力强。

　　5结束语

　　本文针对丝杠进给系统的复杂非线性、多惯量、动态响应较慢和存在时变干扰等问题，依据模糊控制算法，对其模糊控制规则优化设计，提出了一种模糊PI控制策略，和加速度前馈补偿更好地结合，并在Simulink中搭建相应的模型。模糊PI控制一方面简化控制参数整定的流程，使其可以依据偏差e和偏差变化率ec自适应调整自身参数；另一方面从仿真结果看出，改进的模糊PI控制器使被控系统拥有更快的动态响应速度，提升了系统的稳定性和跟踪精度，加速度前馈补偿提升了系统带宽，这基本满足伺服控制的要求。

　　本文的仿真模型是建立在理想环境上，但在实际工作中还存在其他干扰因素，如摩擦损耗、空间谐波、死区时间等情况。综合考虑一系列因素，还需设计摩擦补偿和开发各种先进算法，在DSP数字平台实验验证，以更好地落实到工业化设备中。

       参考文献：

　　[1]陈鹏展,唐小琦,金宏星.伺服系统速度环控制参数自整定方法研究[J].仪表技术与传感器,2010(2):78-81.

　　[2]李文庆,李作庆,王大伟,等.基于参数辨识的交流伺服速度环参数自整定[J].制造技术与机床,2012(4):89-90

　　[3]YU J P,YU H S,CHEN B,et al.Direct adaptive neural control of chaos in the permanent magnet synchronous motor[J].Nonlinear Dynamics,2012,70(3):1879-1887.

　　[4]NORIEGA G,RESTREPO J,BUENO A,et al.Classic,fuzzy and predictive dtc strategies for the PMSM using the bacterial forag-ing algorithmas an online parameter estimator[J].Revista Facul-tad De Ingeniería Universidad De Antioquia,2012(64):182-194.

　　[5]程军涛,刘康华,李雪晓,等.数控机床进给系统王昱忠.伺服系统机械谐振抑制方法的研究与实现[D].沈阳:中国科学院大学(中国科学院沈阳计算技术研究所),2018.

　　[6]石勇.滚珠丝杠进给系统的轨迹跟踪控制方法研究[D].南京:东南大学,2018.

　　[7]周义成.双驱进给系统动态特性评价及优化设计[D].南京:南京理工大学,2018.

　　[8]崔皆凡,马桂新,谢炜.基于模糊滑模观测器的永磁同步电机进给系统速度估计[J].电机与控制应用,2017,44(6):31-34.

　　[9]尉世超,杨振强.基于前馈控制的高精度伺服系统[J].组合机床与自动化加工技术,2022(6):134-137.

　　[10]曹杰铭.基于模糊控制的导弹电动伺服机构控制方法设计与仿真[D].哈尔滨:哈尔滨工业大学,2022.

　　[11]张振鹏,王景成.基于速度加速度前馈和摩擦误差拟合的自适应摩擦补偿研究[C]//2021中国自动化大会论文集,北京,2021:131-137.

　　[12]李亚飞,游有鹏,孙金秋,等.基于惯量辨识的前馈控制算法研究[J].机械制造与自动化,2017,46(5):143-145.

　　[13]李万周,侯伯杰,高建设,等.直线电机速度和加速度的复合前馈控制[J].机床与液压,2015,43(21):146-149.

　　[14]李鑫,杨开明,朱煜,等.平面电机自适应加速度前馈运动控制[J].电机与控制学报,2012,16(9):95-102.