摘要：近年来，随着人们对电子信息隐私及网络安全重视程度的不断提高，对信息加密技术的要求更加严格，图像加密技术备受关注。因此，提出一种基于位平面的图像加密算法。将明文图像矩阵中的每个像素值分解为8个比特位，把相同位置上的比特位组合成高四位和低四位2个位平面矩阵；采用多涡卷混沌系统生成的混沌序列，对2个位平面矩阵进行置乱-扩散-置乱，得到加密图像；在MATLAB平台上进行了直方图、相邻像素相关性、密钥敏感性、信息熵、抗剪裁性等安全性分析。结果表明：所提出的图像加密算法能够进行安全有效的图像加密，且安全分析表示其加密后图像直方图平稳、像素相关性系数趋近于0、信息熵达到7.996 0以上，在加密效果与安全性方面都有良好的表现，可以抵御多种攻击的干扰，能够对图像信息进行安全保护。

　　关键词：图像加密，位平面，行列置乱，混沌，安全性分析

　　0引言

　　随着网络的快速发展，数字图像成为一种便捷的信息传递方式，但是在开放的网络环境中，图像信息的安全性问题受到了极大的挑战[1]。因此，图像加密技术成为信息安全领域的研究热点。

　　由于图像信息含有的数据量较大，且相邻相关性强，所以容易遭受攻击者的破坏[2]。图像加密能够隐藏处理图像中的有效信息，保证图像信息不被他人所利用，从而保证图像数据的安全[3]。混沌系统具有内随机性、初值敏感性与不可预测性等特点，能够产生随机性很强、难以预测的混沌序列，可以应用于图像加密[4]。采用混沌序列对图像的像素值与像素位置进行置换与混淆，可以达到掩盖明文信息的目的[5]。因此，基于混沌系统的图像加密技术在信息安全领域具有较高的研究价值。

　　近年来，随着图像加密技术的不断发展，许多学者在加密算法上进行了长时间的研究与讨论。其中基于位平面的加密算法具有运算速度快、安全性高等特性而受到研究人员的关注[6]。孙夏晨等[7]采用四维超混沌系统生成的混沌序列将比特分解后的图像进行比特置乱操作，然后将加密处理后的图像进行像素值扩散。该算法不仅能够实现密文图像像素值全局置乱，还能有效抵抗差分攻击。孙力等[8]采用Logistic映射产生Arnold参数，对分解后的高4位位平面进行置乱。加密过程简单快捷，适用于对大量图像数据进行加密的场景。Shahna等[9]采用像素值扩散与位平面位置置乱的加密算法，对不同的位平面置乱以减少计算量和提高置换效率，使密文图像中的像素值具有很强的随机性。伍朝阳等[10]采用超混沌Chen系统产生混沌序列，依据不同的混沌序列实现图像像素层和比特层的全局置乱。该算法不仅提高比特值的扩散程度，还能够有效改变像素位置。方鹏飞等[11]利用图像像素通过散列函数得到二维Logistic混沌初始参数，产生的密钥与DNA序列和Feistel分组加密网络结合对灰度图像进行加密，使图像可以抵抗各种统计攻击。唐传华等[12]运用Logistic-Sine混沌映射迭代生成混沌序列，对图像采用全局置乱、比特平面的交叉换位，以及异或扩散的加密算法得到密文图像。该算法能够增强破解密文图像的复杂程度。

　　结合文献[7-12]对位平面加密算法的研究，本文提出一种新的基于位平面的图像加密算法。该算法利用位平面所含信息量的不同，首先将图像矩阵分解成高四位与低四位2个矩阵，然后结合混沌系统产生的多个混沌序列，对2个矩阵分别进行置乱与扩散操作，最后利用位平面的合并将加密后的2个矩阵合成密文图像。加密后的图像在安全性、复杂度等方面都表现出了优良的特性，既能保证图像的安全性，又能够提高加密系统的效率。

　　1位平面特性

　　给定一幅灰度图像，将图片中的像素值转换成二进制位数，相同位数上的比特（表示为0或1）组成的平面即为位平面[13]。输入一副大小为M×N、灰度级为256的灰度图像，利用式（1）计算得出每个位平面的比特值。

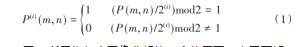
　　图1所示为灰度图像分解的8个位平面。由图可知，每个位平面所含有的明文图像信息各不相同，从第8位位平面到第5位位平面虽然清晰度越来越差，但可以看出图像的大致轮廓，从第4位位平面到第1位位平面已无法看清图像的有效信息，说明低四位位平面图像所含有的明文信息量极少。

　　根据不同位平面图像含有信息量的不同，计算每个位平面所占明文图像信息的比例。其计算方法如下：

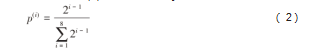
　　式中：p(i)为第i位平面所占明文图像信息的比例。

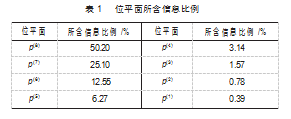
　　表1所示为不同位平面所含原图像信息的百分比。由表可知，随着位数的不断减小，位平面所含的信息量逐级减少。因为高位位平面含有较多的信息，所以本文对高四位图像的像素值进行置乱与扩散操作，加密效果更明显有效。

　　2图像加密算法
       2.1算法原理

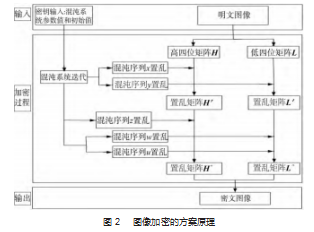
　　本算法将明文图像上的像素值经过位平面分解，针对位平面的特征，设计不同强度的加密算法对数字图像的信息进行隐藏，其原理如图2所示。

　　2.2加密过程

　　加密过程步骤如下。

　　步骤1：输入8位M×N灰度明文图像P。

　　步骤2：将待加密图像P，利用位平面分解，生成2个4位M×N矩阵H（高四位矩阵）和L（低四位矩阵）。

　　步骤3：输入混沌系统密钥，通过迭代1 000+M×N次，舍去混沌序列前1 000个值以消除暂态反应，得到5个长度为M×N的一维混沌序列（x,y,z,w,u）。

　　步骤4：将混沌序列x根据数值大小，由小到大的顺序进行排列，获得新序列x'和一组位置序列T={T1,T2,T3,…,TM×N}。

　　步骤5：利用位置序列T对高四位矩阵H进行位置置乱，得到置乱矩阵H'，置乱方程式如下。

　　Hi'=HTi（3）

　　步骤6：同理将混沌序列y从小到大排列得到位置序列K，利用位置序列K对低四位矩阵L进行位置置乱，置乱方法同式（3），得到矩阵L'。

　　步骤7：利用式（4）对混沌序列z进行处理，得到一个随机整数序列，通过式（5）转化为M×N的矩阵z"，并将z"分解成2个4位的M×N矩阵HT和LT。

　　z'=mod(mod(floor(z(1 000+1:1 000+M×N)×1014),10 000),256)+1（4）

　　z"=reshape(z',N,M)（5）

　　步骤8：通过式（6）对矩阵H'进行像素值扩散，得到加密后的高四位矩阵H"。

　　H"(i,j)=bitxor(H'(i,j),HT(i,j))i∈(1,M),j∈(1,N)（6）

　　步骤9：将混沌序列w随机取N个数为序列w'，通过式（7）对w'序列进行取整，得到一个0~(M-1)的随机整数序列w"=(w"1,w"2,w"3,…,w"N)。

　　w"=mod(mod(floor(w'×1014),10 000),M)（7）

　　步骤10：列移位位置置乱。运用混沌序列w"，对其进行列移位，加密矩阵共有N列，对矩阵的每一列向下移对应的w"(i)位（i=1,2,…,N），从而达到每一列像素值位置置乱。

　　步骤11：将混沌序列u随机取M个数为序列u'，通过式（8）对u'序列进行取整，得到一个0~（N-1）的随机整数序列u"=(u"1,u"2,u"3,…,u"M)。

　　u"=mod(mod(floor(u'×1014),10 000),N)（8）

　　步骤12：行移位位置置乱。经过对低四位矩阵的列移位处理后，运用混沌序列u"，对其进行行移位，加密矩阵共有M行，对矩阵的每一行向右移动对应的u"(i)位（i=1,2,…,M），达到每一行像素值位置置乱，得到加密矩阵L"。

　　步骤13：将高四位矩阵H"和低四位矩阵L"合成一个8位矩阵，得到加密矩阵C。

　　2.3仿真实验

　　为了验证加密算法的性能，采用文献[14]所设计的多涡卷混沌系统来产生混沌序列，用于图像加密。选取标准256 Pixel×256 Pixel的Lena等4幅灰度图像作为加密程序的实验图像。图3所示为经过本算法加密或解密后的图像。由图可知，该算法能够将图像中的有效信息进行掩盖，并能够将加密后的图像进行还原，验证了该算法的有效性与安全性。

　　3加密安全性分析
       3.1灰度直方图

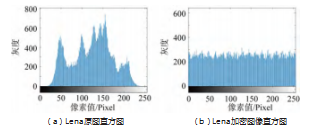
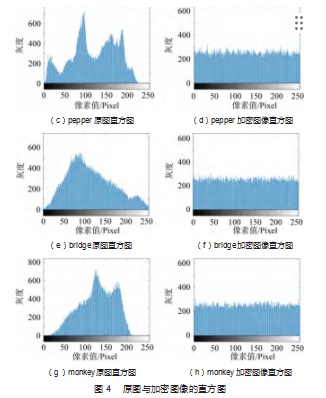
　　图像的直方图可以反映像素值的分布情况，是一种十分重要的图像分析工具[15]。直方图分布越均匀，说明加密效果越好。图4所示为明文图像和密文图像的灰度直方图。由图可知，原图像像素值分布不均匀，具有很高的像素相关性，容易被攻击者利用统计分析进行攻击，而加密后的图像直方图分布均匀，有效地将明文图像分布的灰度值进行掩盖隐藏，使文中密文图像的像素相关性有所降低，增加了破译图像信息的难度。说明文中算法能够很好地抵挡统计攻击，增加了破译难度。

　　3.2相邻像素的相关系数

　　数字图像数据有较高的冗余度，相邻像素相关性强，攻击者可以利用像素相关性进行攻击[16]。为了分析文中算法的相邻相关性，在4张实验图像中，分别从原始图像与加密图像随机抽取1 000个像素点，并将其作为实验数据，统计明文图像与密文图像各个方向上的相关性，计算公式如下：

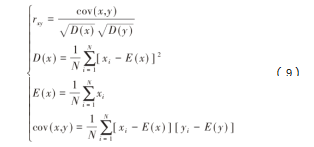
　　式中：rxy为相关系数；D(x)为方差；E(x)为均值；cov(x,y)为x和y的协方差；N为图中所取像素点的对数[17]。

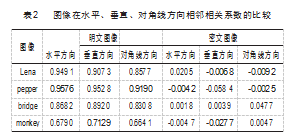
　　表2所示为明文图像和密文图像在水平方向、垂直方向和对角线方向的相关系数。由表可知，明文图像的相邻相关系数较大且接近于1，而密文图像各个方向上的相关系数较小并且趋于0，说明该算法降低了图像中的像素相关性。

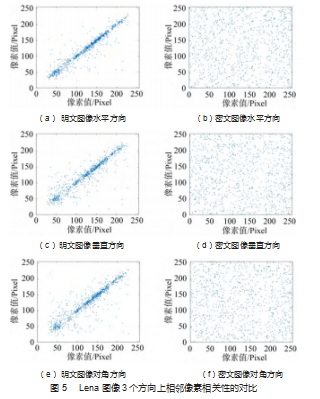
　　为了更加直观地看出实验结果的像素相邻相关性，对Lena原图和加密图像在水平、垂直和对角线3个方向的像素分布情况进行了绘图，如图5所示。由图可知，明文图像相邻像素在水平方向、垂直方向和对角线方向上的相邻像素呈线性分布且相关性强。而密文图像相邻像素在3个方向上分布均匀且无规律可循，相关性较弱，说明明文图像的统计特性已很好地扩散到密文图像中，提高了图像抵抗统计分析攻击的能力，具有良好的安全性与实用性。

　　3.3密钥敏感性

　　当未被扰动的密钥与存在微小扰动下的密钥同时对密文图像进行解密时，通过对比两者得到的解密图像的差异程度来衡量密钥的敏感性[18]。如果两者差异显著，说明该算法具有较好的敏感性。像素变化比率QNPCR和归一化平均变化程度QUACI可以用来评价算法的加密敏感性，其计算公式如下：

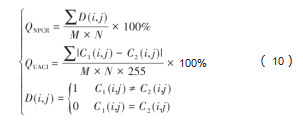
　　式中：M、N为图像大小；C 1(i,j)、C2(i,j)为2个密文图像。

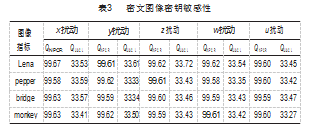
　　QNPCR的理论值为99.6094%，QUACI的理论值为33.463 5%[14]。为了评估本算法的加密敏感性，在图像加密过程中，分别对5个初值加以微弱扰动（数量级10-15），其他参数保持不变，相应的测试结果如表3所示。由表可知，密文图像的QNPCR和QUACI均接近理想值，证明了文中算法在加密过程中具有良好的敏感性。

　　可知，对其中一个参数加以扰动，解密后的图像均不能还原为明文图像，同样说明了文中算法具有良好的解密敏感性。

　　3.4图像信息熵

　　信息熵作为像素值信息含量的量化指标，用来衡量加密图像中信息的随机性[19]，其计算方法如下：

　　式中：L为灰度级层数；p(xi)为灰度值xi出现的概率。

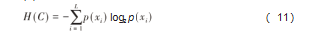
　　对于灰度图像来说，像素值为0~255 Pixel的随机整数，H的理论值为8，明文图像与密文图像的信息熵如表4所示。由表可知，明文图像与密文图像信息熵的数值差距，并且密文图像的信息熵趋近于理论值。

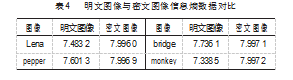
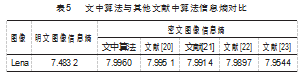
　　以Lena图像为例，表5所示为文中算法的信息熵与其他文献算法的信息熵。由表可知，文中算法的信息熵更接近于理论值，说明经过该算法可获得更好的加密效果。

　　3.5抗剪裁分析

　　在图像的传输过程中，图像的部分数据可能会丢失，因此需要进行抗剪裁分析。使用Lena图像作为测试图像，随机的将密文图像中部分像素值置成0，并对剪裁后的密文图像进行解密操作。图7所示为对加密图像采取不同比例剪裁的密文图像以及对应剪裁后的解密图像。由图可知，随着裁剪面积的不断增大，经过解密后的图像依然能够保留原图像的有效信息。说明该算法在受到不同面积的裁剪攻击时，依然可以保证图像信息的安全传输，具有良好的抗剪裁能力。

　　4结束语

　　本文提出了一种基于位平面的图像加密算法，首先将图像矩阵通过位平面的特性分解成高四位与低四位2个矩阵，然后利用位平面所含信息量的不同，结合混沌系统产生的多个混沌序列，对2个矩阵分别进行置乱与扩散操作，最后利用位平面的合并将加密后的2个矩阵合成密文图像，实现对图像信息的加密操作，并对密文图像的安全性能进行理论分析和数值仿真。仿真结果验证了该算法具有较高的安全性。因此，所提算法可以有效保护数字图像安全传输，在图像加密、保密通信等领域有着良好的实用价值和广阔的应用前景，能够广泛应用于图像安全领域中，为图像加密算法研究提供了新思路。

　　参考文献：

　　[1]赵智鹏,周双,王兴元.基于深度学习的新混沌信号及其在图像加密中的应用[J].物理学报,2021,70(23):139-153.

　　[2]李春彪,赵云楠,李雅宁,等.基于正弦反馈Logistic混沌映射的图像加密算法及其FPGA实现[J].电子与信息学报,2021,43(12):3766-3774.

　　[3]LIU Y,TONG X J,MA J.Image encryption algorithm based on hyper-chaotic system and dynamic S-box[J].Multimedia Tools and Applications,2016,75(13):7739-7759.

　　[4]YE G D,HUANG X L.A novel block chaotic encryption scheme for remote sensing image[J].Multimedia Tools and Applications,2016,75(18):11433-11446.

　　[5]陈虹,赵菊芳,郭鹏飞,等.基于混沌映射的分块循环DNA图像加密算法[J].计算机应用研究,2022,39(6):1865-1871.

　　[6]袁源,和红杰,陈帆.减少相邻位平面间冗余度的加密图像可逆信息隐藏[J].中国图象图形学报,2019,24(1):13-22.

　　[7]孙夏晨,明鹏,李文石.基于比特全置乱的超混沌图像加密算法[J].电子测量技术,2021,44(12):128-132.

　　[8]孙力,梁立.基于位置换的混沌对称图像加密算法[J].计算机应用与软件,2015,32(7):305-309.

　　[9]SHAHNA K U,MOHAMED A.A novel image encryption scheme using both pixel level and bit level permutation with cha-otic map[J].Applied Soft Computing,2020,90:106162.

　　[10]伍朝阳,孙树亮,刘庆.基于像素层与比特层置乱的超混沌图像加密算法[J].中国科技论文,2018,13(14):1609-1613.

　　[11]方鹏飞,黄陆光,娄苗苗,等.基于二维Logistic混沌映射与DNA序列运算的图像加密算法[J].中国科技论文,2021,16(3):247-252.

　　[12]唐传华,巫朝霞.Logistic-Sine映射与比特重组的图像加密算法[J].智能计算机与应用,2022,12(3):173-179.

　　[13]施飞,张红梅,张向利.基于混沌映射和DNA编码的图像加密算法[J].计算机工程与应用,2018,54(5):91-95.

　　[14]刘嵩,韦亚萍,刘静漪,等.一种新的多涡卷混沌模型在图像加密中的应用[J].华中师范大学学报(自然科学版),2020,54(1):36-44.

　　[15]汪勍,徐国天.基于改进Logistic映射和双图混合的加密算法[J].信息网络安全,2022,22(12):76-86.

　　[16]陈森,薛伟.基于混沌和DNA随机编码的彩色图像加密算法[J].传感器与微系统,2021,40(8):144-147.

　　[17]李振宇,张昊,王莉,等.基于分数阶混沌系统和RNA编码的立体图像加密算法[J].太原理工大学学报,2021,52(5):718-727.

　　[18]刘静漪.基于混沌系统的数字图像加密算法研究[D].恩施:湖北民族大学,2019.

　　[19]黄林荃,刘会,赵波.数字图像空域加密技术综述[J].计算机技术与发展,2021,31(1):137-141.

　　[20]刘思聪,李春彪,李泳新.基于指数-余弦离散混沌映射的图像加密算法研究[J].电子与信息学报,2022,44(5):1754-1762.

　　[21]李付鹏,刘敬彪,王光义,等.基于混沌集的图像加密算法[J].电子与信息学报,2020,42(4):981-987.

　　[22]张勋才,刘奕杉,崔光照.基于DNA编码和超混沌系统的图像加密算法[J].计算机应用研究,2019,36(4):1139-1143.

　　[23]刘瀚扬,华南,王一诺,等.基于量子随机行走和多维混沌的三维图像加密算法[J].物理学报,2022,71(17):140-155.