摘要：针对目前风能、光能、柴油发电机组多能互补模型中考虑弃风光能源的浪费，在系统构建中加入电解水制氢系统和氢燃料电池系统，利用可再生能源弃电实现零碳排放制氢，增强新能源电力的消纳，建立电力系统经济调度模型。将电解水制氢系统、氢燃料电池与风光火多能互补电力系统结合，利用电力系统满足负荷后多余的可再生能源弃电进行电解水制氢，并利用氢燃料电池对不足的电力进行补足，辅助火电机组进行调峰，氢储能的加入能够提升系统对其孤岛环境的电力供应能力。提出基于一种改进非支配排序遗传算法2(NSGA2)来求解目标函数，利用测试函数对改进前后的算法进行性能测试，通过实例数据进行模拟仿真，仿真结果表明，在不增污染气体排放量的同时降低了燃料费用，验证了在解决电力系统经济调度问题方面的可行性和有效性。

　　关键词：多能互补，经济调度，多目标优化，NSGA2;，新能源消纳

　　0引言

　　作为世界上最大的碳排放国，发展低碳经济是我国必由之路。基于风能和太阳能的可再生能源是绿色、低碳、取之不尽的。然而，随着风能和光伏发电装机容量规模逐年上升，弃风光清洁能源的浪费是无法避免的。

　　电力系统的正常运行的关键一环即为电力系统的调度，调度问题包括经济性、环保，在系统满足各种等式及不等式的约束下，最大限度地提升系统的经济性，即令系统总的发电成本最小。其内在含义为最值寻优问题。

　　现有多能互补集成系统仿真模型研究主要用于可行性和经济性分析、能量管理和容量配制优化两方面。荆涛等[1]针对风力发电和光伏发电出力不确定性，在成本目标函数中加入火电机组排污惩罚及风电和光伏发电备用容量惩罚。张倩文[2]遵循清洁能源之间的互补特性，模型验证了利用能源的互补性可降低火电机组的出力波动，为电网提供更加稳定的电能。Li P等[3]综合考虑了环境效益和经济效益，利用改进的含动态约束处理能力的多目标差分进化算法，提高了全局最优解的搜索能力。

　　Lin L等[4]针对电网成本低、环境友好的多目标问题，利用小概率变异机制，采用拥挤举例排序方法，提高了算法搜索能力。檀勤良等[5]以企业购电成本最小、可再生能源发电量最大、可再生能源出力波动性最小为目标构建了风光火电联合调度多目标优化模型，验证了模型在促进可再生能源消纳和节能减排方面的作用。林俐等[6]建立了以改善净负荷峰谷波动性最优、抽蓄调用效益最大、系统总调峰成本最小为目标的抽蓄－火电联合调峰分层优化调度模型。贾成振等[7]提出了一种带有需求侧响应的最优分配方法，基于风氢耦合发电系统的仿真模型，采用最优容量分配和快速遗传算法(NSGA-II)进行日前调度。陈维荣等[8]针对多能互补微电网经济成本最优问题，提出一种计及需求侧响应的风－光－氢多能互补微电网优化配置方法。赵书强等[9]提出了综合考虑风光储调度出力曲线与计划出力曲线匹配程度、储能电池充放电功率的平缓程度及储能电池的可持续工作性能的储能优化调度模型。杨晓萍等[10]提出了一种基于分时电价和虚拟电厂的风光火储系统两阶段优化模型。目前关于含储能单元的多能互补优化调度研究已经取得了一定的成果。孟现峰等[11]搭建了包含电解槽、储氢罐、质子交换膜燃料电池等部件的集成系统，并设计了各组成单元能量控制策略。秦梦珠等[12]提出了一种新型风电－氢能耦合系统，在并网模式时利用多余电能电解水制氢，离岛独立运行模式时解决系统能量平衡、提高供电质量等问题。实际上，由于电能无法直接存储，电网消纳能力补足带来的弃风、弃光问题也是风能、太阳能开发利用中的痛点。因此，储能系统是可再生能源开发中的关键技术，其通过充电、放电的削峰填谷作用可以实现对电力系统功率和能量的转移存储，从而有效缓解可再生能源开发中的弃电问题[13]。

　　本文利用风力、太阳能、柴油发电机、电解槽和氢燃料电池构建了多能源互补的电力系统经济调度模型。该模型同时考虑了污染排放和经济性。其次，本文对NSGA2算法进行了改进。选取了在多目标优化领域常用的经典ZDT系列测试函数对改进前后的算法进行性能分析，为电力系统经济调度提供了更好的算法选择。最后，本文利用实例数据进行模拟仿真，实验的结果表明，利用改进的NSGA2优化算法对运行成本、污染排放成本进行优化，在解决经济调度问题方面的可行性和有效性，在不增污染气体排放量的同时降低了燃料费用。

　　1电力系统经济调度模型

　　1.1多能互补系统结构

　　本文基于风、光、柴油发电机组模型的基础上在系统构建中加入了电解水制氢系统和氢燃料电池系统，利用可再生能源弃电制氢便是解决弃风弃光问题的关键所在。在模型构建中充分考虑了系统各部分的运行成本，

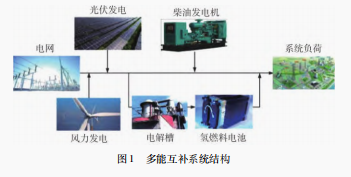
　　同时考虑以总经济运行成本和污染排放作为多目标优化模型。为了灵活调节各发电机组出力，并提高风光消纳水平，多能互补系统结构如图1所示。本文电力系统工作模式为多能互补系统发电，与系统负荷相比，当有多余电量时电解水制氢，由氢燃料电池储存；若发电量无法满足负荷，不足部分由氢燃料电池补足，仍有不足则由柴油发电机组补足。

　　1.2机组运行模型

　　1.2.1风力机组模型

　　风力机组的出力由轮毅处的风速决定。风电的输出功率与其当前段的风速有关。其功率－风速关系曲线如图2所示。

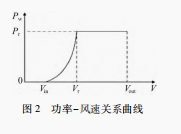
　　当风速小于或等于风力发电机的切入风速vin时，此时，风力发电机不工作；继续增大风速，但小于或等于风力发电机的额定风速vr时，此时，风机出力以图中的曲线趋势增大；继续增大风速，但小于或等于风力发电机的切出风速vout时，此时，风机出力恒定；继续增大风速，风力发电机将停止工作。风力发电机数学模型[14]如式(1)所示：

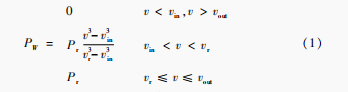
　　式中：Pr风机额定输出功率；v in切入风速；v out切出风速；v r额定风速。风力单元成本如式(2)所示：

　　Cf(t)=dfPW(t)(2)

　　式中：df为风力发电机的运行成本系数。
       1.2.2光伏发电模型
       光伏单元符合以下模型[15],光伏组件温度如式(3)所示：

　　Tc=Tand+kGAC(3)

　　式中：Tand为环境温度；GAC为接收的太阳辐射量；k为常量。光伏组件的输出功率如式(4)所示。

　　式中：PSTC光伏组件最大测试功率；G STC为标准测试下的光照强度，取1000 W/m2;KT为功率温度系数，取值范围为-0.47~0.5%/℃;Tτ为参考温度，取25℃。

　　光伏单元成本如式(5)所示：

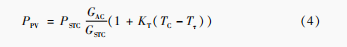
　　式中：dPV为光伏发电的运行成本系数。

　　1.2.3柴油发电机组模型

　　柴油发电机组方面利用常规发电单元的运行成本函数[16],以二次函数形式描述，常规发电机组发电经济成本实质就是运行期间机组消耗燃料的费用，与机组输出功率有关，具体模型如式(6)所示：

　　CH(t)=a i P(t)+b i PH(t)+c i(6)

　　式中：a i、b i、c i为柴油发电机组的成本系数；PH(t)

　　为单位时间内的柴油发电机组出力。污染排放成本与机组PH发电出力可以近似视为二次线性函数的关系如式(7)所示：

　　C2=αi P(t)+βi PH(t)+γi(7)

　　式中：αi、βi、γi为柴油发机组单位出力污染系数。

　　1.2.4电解槽系统模型

　　当风光火发电机组负荷大于系统负荷时，有多余的可再生能源，此时就利用电解槽电解水制氢[17],电解槽输入功率如式(8)所示：

　　PE(t)=max[0,(Pw(t)+PPV(t)+PGi(t)-PLoad(t)ξ)ηE](8)

　　式中：PLoad(t)为t时刻的系统负荷；ξ为多能互补发电系统满足的负荷比例；ηE为电解槽的能量转化效率。电解槽单元成本如式(9)所示：

　　CE(t)=dE PE(t)(9)

　　式中：dE为电解槽运行成本系数。

　　1.2.5氢燃料电池模型

　　系统负荷与风光火发电机组负荷作比较，若发电量无法满足系统负荷，不足部分由氢燃料电池补足，氢燃料电池的输入功率如式(10)所示：

　　PFC(t)=min[PFCmax,Max[0,PLoad(t)ζ-Pw(t)-PPV(t)-PGi(t)]](10)

　　式中：PFCmax为氢燃料电池的最大输出功率。氢燃料电池单元成本如式(11)所示：

　　CFC(t)=dFC PFC(t)(11)

　　式中：dFC为氢燃料电池运行成本系数。

　　1.2.6弃风光成本模型

　　引入弃风、光惩罚成本，用以保证可再生能源的高比例渗透需求，风、光惩罚成本计算函数[18]如式(12)所示：

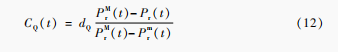
　　式中：dQ为弃风、光成本特性参数；P、P为可再生发电单元出力的上限和下限。1.3优化目标及约束条件提出了一种兼顾经济性和污染排放的电网系统经济调度模型。用于仿真的电力系统模型由风能、太阳能、柴油发电机、电解槽和氢燃料电池组成，氢燃料电池的加入使电网系统能够实现多能源互补。

　　目标函数一：系统成本是所有发电机成本的总和如式(13)所示：

　　minC1=Cf(t)+CPV(t)+CH(t)+CE(t)+CFC(t)+CQ(t)(13)

　　目标函数二：污染排放如式(14)所示：

　　minC2=αi P(t)+βi PH(t)+γi(14)

　　希望能够实现在总的运行成本最小的同时，污染排放量也尽可能的少，即多个目标如何同时实现最优。

　　能源调度的前提是供配电系统能够始终稳定可靠地运行，这就需要保证电力系统负荷始终保持平衡，电力系统负荷平衡如式(15)所示：

　　PW(t)+PPV(t)+PH(t)+PE(t)+PFC(t)=PLoad(t)(15)

　　所有发电机不能超过各自的发电能力如式(16)(20)所示：

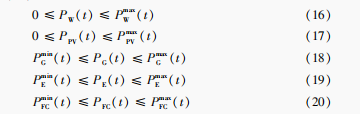
        (20)式中：P(t)为风电机组最大出力功率；Px(t)为光伏发电最大功率；Pin(t)、Pax(t)分别为柴油发电机组最小、最大功率；Pin(t)、Pax(t)分别为电解槽最小、最大功率；Pn(t)、Px(t)为氢燃料电池最小、最大功率。

　　2模型求解

　　2.1 NSGA2算法

　　NSGA算法是Goldberg提出的一种适应度共享技术，这种算法是基于非支配性排序的原则，对种群中的个体进行分类，以获得一个具有均匀分布的帕累托最优或非支配性的解决方案。然而，这种算法的缺点是计算成本高，分布的参数需要人为设置等。NSGA2算法凭借简单和高效的优势，NSGA2算法已经成为最受欢迎的MOEA算法之一，NSGA2仍然是最好的进化多目标算法之一，现在被广泛用作科学计算、工程设计和其他领域中解决多目标优化问题(MOP)的有效方法[19]。

　　NSGA2具体算法流程如图3所示。

　　STEP1：首先，初始化种群，随机生成父代。

　　STEP2：对父代存放的数值进行非支配排序，求出个体之间的支配关系并找出属于第一支配前沿的个体。遍历群体中的每个个体p,遍历的时候做两个工作：(1)

　　计算支配当前个体的解决方案数量np;(2)找出被当前个体支配的个体，并将它放入集合Sp中。对当前个体来说，如果群体中的其他个体都不能支配它（即np=0),那么这个个体就属于第一支配前沿，将其放入集合F1中。

　　STEP3：计算拥挤距离，参数都为属于同一个支配前沿的个体集合Fi。因为有m个目标函数，所以对于每个函数该个体的拥挤距离都不同，因此需对所有个体进行排序。

　　STEP4：采用二元锦标赛选择、均匀交叉和单点变异的方法，由父代种群产生第一代子群。

　　STEP5：此时迭代次数加一，将得到的父代与子代进行合并，重复上述快速非支配排序与拥挤度计算，通过精英保留机制选择合适的个体组成新的父代，判断是否达到最大迭代次数，当条件满足时，循环结束。

　　2.2 INSGA2算法

　　NSGA2算法有一些缺点，如对于一些具有复杂帕累托边界、高维多变量和复杂非线性的多目标问题，拥挤距离公式不够充分，而且拥挤距离公式只考虑相邻个体之间的距离，不同子目标上的拥挤距离差异很大。无法获得较多的遗传机会，不利于解集分布性的维护。传统距离公式如式(21)所示。

　　式中：f是第k个的第j个目标函数值；f和f分别是第j个目标函数的最小值和最大值；m是目标函数的个数。

　　因此本文考虑一种基于方差的新型拥挤距离，提高算法的收敛性与分布性，其计算公式如下：

　　关于电力系统的多目标优化的流程如图4表示。

　　3算法测试及结果分析

　　为了验证改进后的INSGA2算法性能，将NSGA2算法进行对比数值实验仿真。本文选取在多目标优化领域常用的4个经典ZDT系列[20]函数进行测试，其中包括ZDT1、ZDT2、ZDT3、ZDT6测试函数。

　　3.1实验参数

　　为对比改进前后的算法方面的收敛性与分布性，对两种算法均做如下参数设置：种群大小规模为100,最大迭代次数为200,遗传部分的操作选取的均匀交叉和均匀变异，交叉概率为0.7,变异概率为0.4,其中，ZDT系列测试函数的决策变量大小规模都可以随意设置，本文中选取的决策变量规模均为10。

　　3.2实验结果及分析

　　为了验证改进后的INSGA2算法的性能，数值仿真结果如下，图5~8为ZDT系列函数测试结果。

　　求解ZDT1问题时，改进前后的算法解集的收敛性和分布性相差不多；在求解ZDT2问题时，可以看到改进后的INSGA2算法略微更接近真实的Pareto边界；求解ZDT3问题时，ZDT3测试函数是不连续的Pareto边界，对比改进前后的算法观察到都可以较好地收敛到其真实的边界；求解ZDT6问题时，可以明显地观察看出对比改进前的算法，其改进后的算法解集收敛性明显优于原算法。因此，从总体的测试结果来看，改进后的INSGA2算法的优化性能优于传统NSGA2算法。

　　4算例分析

　　利用北方某地近1a逐时实例数据（平均温度、平均风速、辐射强度）进行模拟仿真，数据都通过Meteonorm气象软件获取。风机、光伏系统参数如表1~2所示。

　　各机组参数如下：柴油发电机组成本系数ai、b i、c i分别选取11.6581、7.4961、0.001 73,污染系数αi、βi、γi分别选取为3.339 08、-0.425 6、0.064 90;多能互补发电系统负荷比例ξ为0.8,电解槽的能量转化效率ηE为0.7;氢燃料电池的最大输出功率PFCmax=10 MW,各机组成本系数dE、dFC、dQ分别为0.57、0.66、0.05。

　　其中风机、光伏出力功率曲线取自2021北方某地区逐月平均温度、风速、辐射强度的数据，功率随月份变化如表3所示。

　　图9为依据表3绘制的风机光伏随月份变化的出力功率曲线。设定系统由3台风力发电机、3台光伏发电机、5台柴油发电机、1台电解槽和1台氢燃料电池，针对一个时间断面进行有功调度分配。设定自变量以及取值范围风速范围0~20 m/s,柴油发电机组功率10 MW,太阳辐射量0~1 700 W/m2,环境温度-10~30℃,系统负荷50 MW。设定种群大小为50,最大迭代次数为100,交叉概率为0.7,变异概率为0.4。最后得到仿真结果如图10所示。

　　优化结果如表4所示，帕累托两端分别对应最小污染排放和最小运行成本，可见，相比于传统NSGA2算法所得的最少污染排放和最低运行成本方案，详细如表5~6所示。与改进算法相比，INSAG2解的准确性和多样性优于NSGA2解，而且得到更均匀分布的帕累托前沿曲线。从解决方案上来看，本文改进后的INSGA2解的分布性和收敛性优于传统NSGA2算法，在运行时间上，INSGA2也比NSGA2快0.3 s左右；在最少污染排放方面，改进前后的算法相差0.059 5 t/h;在最小运行成本方面，改进前后的算法减少了5.701USD/h。

　　5结束语

　　本文利用可再生能源弃电制氢，在系统构建中考虑了风机、光伏、柴油发电机、电解槽和氢燃料电池，在发电机组出力约束上下限内，建立电力系统多目标经济调度模型。利用一种基于方差的新型拥挤距离公式的改进NSGA2算法对运行成本、环境成本进行优化，生成帕累托最优解集。仿真结果表明，本文算法运行时间短，收敛快，且得到分布特性良好的帕累托最优前沿。在解决实际经济调度方面问题时，在尽可能使运行成本最小的同时考虑了污染排放问题，并利用所改进的NSGA2算法进行多目标优化。结果表明，该方法可以为决策者提供多种最优解集供其选择，并证明了改进算法的可行性和有效性，在不增污染气体排放量的同时降低了燃料费用。

　　参考文献：

　　[1]荆涛，陈庚，王子豪，等．风光互补发电耦合氢储能系统研究综述[J].中国电力，2022,55(1):75-83.

　　[2]张倩文，王秀丽，李言．含风光水储互补电力系统的优化调度研究[J].电力与能源，2017,38(5):581-586.

　　[3]Li P,Dond R,Wang L,et al.Multi-energy coordinated operation optimization model for wind-solar-hydro-thermal-energy storage system considering the complementary characteristics of different power resources[C]Ⅱ2018 2nd IEEE Conference on Energy Internet and Energy System Integration(EI2).Beijing,China:IEEE,2018:1-6.

　　[4]Lin L,Yue X Y,Xu B Q,et al.Sequence and strategy of pumped storage-thermal combined peak shaving considering benefits of pumped storage and deep regulation of thermal power[J].Power System Technology,2021,45(1):20-32.

　　[5]檀勤良，丁毅宏，李渝，等．考虑经济－环境平衡的风光火联合外送调度策略多目标优化[J].电力建设，2020,41(8):129-136.

　　[6]林俐，岳晓宇，许冰倩，等．计及抽水蓄能和火电深度调峰效益的抽蓄－火电联合调峰调用顺序及策略[J].电网技术，2021,45(1):20-32.

　　[7]贾成真，王灵梅，孟恩隆，等．风光氢耦合发电系统的容量优化配置及日前优化调度[J].中国电力，2020,53(10):80-87.

　　[8]陈维荣，傅王璇，韩莹，等．计及需求侧的风－光－氢多能互补微电网优化配置[J].西南交通大学学报，2021,56(3):640-649.

　　[9]赵书强，刘大正，谢宇琪，等．基于相关机会目标规划的风光储联合发电系统储能调度策略[J].电力系统自动化，2015,39(14):30-36,53.

　　[10]杨晓萍，刘浩杰，黄强．考虑分时电价的风光储联合“削峰”优化调度模型[J].太阳能学报，2018,39(6):1752-1760.

　　[11]孟现锋，罗勇，Crisalle O D.风电氢联产系统功率平滑控制仿真研究[J].可再生能源，2016,34(11):1595-1602.

　　[12]秦梦珠，张国月，齐冬莲．风电－氢能耦合系统建模及仿真[J].电子技术，2016,45(8):18-23.

　　[13]Ding Z Y,Hou H J,Yu G,et al.Performance analysis of a wind-solar hybrid power generation system[J].Energy Conversion and Management,2019,181(2):223-234.

　　[14]Ju L,Zhao R,Tan Q,et al.A multi-objective robust scheduling model and solution algorithm for a novel virtual power plant connected with

　　power-to-gas and gas storage tank considering uncertainty and demand response[J].Applied Energy,2019,250:1336-1355.

　　[15]Zhao Xingang,Zhang Zeqi,Meng Jin,et al.Economic-environmental dispatch of microgrid based on improved quantum particle swarmoptimization[J].Energy,2020,195(3):1-15.

　　[16]朱能能，刘闯，夏克勤，等．考虑分时电价和分布式储能的主动配电网经济优化调度[J].内蒙古电力技术，2023,41(5):54-61.

　　[17]邵志芳，张东强．基于合约负荷曲线的多能互补电力系统容量优化配置[J].电网技术，2020,45(5):1757-1767.

　　[18]刘志坚，王旭辉，郑超铭．计及可再生能源发电成本的智能电网分布式经济调度[J].电子测量技术，2020,43(2):84-90.

　　[19]李先允，冯瀚飞．基于NSGA2算法的燃料电池系统净功率优化[J].电源技术，2023,47(1):83-87.

　　[20]DEB K.Multi-objective genetic algorithms:Problem difficulties and construction of test problems[J].Evolutionary computa-tion,1999,7(3):205-230.