摘要：“拍照赚钱”是移动互联网模式下的一种自助式劳务众包平台，为企业提供了各种商业检查和信息搜索。APP中的任务定价是该平台的核心要素，任务定价的合理性与否将会直接决定商品检查的成功与否。本文依据某平台所给出的任务数据，结合任务所在经纬度、定价、会员信息数据等研究项目中的任务定价规律，并根据分析结果，定量分析任务未完成的原因。在现实生活中，由于任务分布的不均匀性，存在争抢任务的现象，因此，自助式劳务众包平台将距离较近的几个任务打包发布。本文研究了在“打包”情景下，定价模型有何变化，需要如何进行修改，修改后的模型对最终任务完成的情况又有什么影响。最后，结合分析，对原有项目制定新的任务定价方案，并结合实际情况与预计模型的结果，分析评价该方案的实施效果。

　　关键词：“拍照赚钱”；APP；定价规律；参数优化；回归模型

　　一、研究设计

　　首先对APP内给出的数据经纬度进行分析，定位该APP所在的区域为广东省，其中任务和会员的分布地点为广州市、佛山市、东莞市及深圳市。将任务的完成情况、会员的地理位置重叠到同一个维度下，利用MATLAB软件，可求得会员所在位置的中心点和任务所在中心点重合，该中心点对应的纬度为22.9825，经度为113.5375。

　　由于互联网模式下的劳务众包平台，近似为完全竞争市场，即买卖双方所获得的信息是完全一致的。故本文以任务点和会员点到中心点的相对距离量化两者之间的地理位置关系，进而建立模型探究由于位置差异导致的价格成本。首先运用MATLAB画出了任务完成情况下价格与相对距离的散点图，从图像上可知距离和价格的函数关系为分段函数。为进一步得出分段函数的具体表达式，先求出每段分段函数的相对距离的平均值，再利用MATLAB函数拟合工具[2]，剔除两个偏离程度很大的数据，得到初步的拟合函数如下：

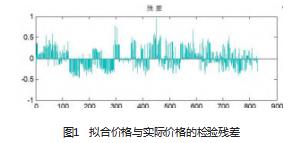
　　对该拟合模型的残差进行分析可知，初步拟合的模型拟合效果并不是很好。可能是在初期数据的处理上，仅选择了平均值代替，残差模较大。同理依次遍历指数、对数、二项式等拟合模型，最终确定价格与相对距离之间呈线性关系。

　　二、定价模型的建立

　　基于上述初步分析，笔者发现APP内的原定价方案中，价格是不连续的分段函数。但是实际的定价过程中，价格的制定需要考虑地形、商业区的分布、交通的便利程度等，以期达到市场的供给与需求的平衡。由此定义β系数为区域综合的价格调整系数，该系数包含了地形、商业区的分布、城市文化差异、消费水平等诸多因素对价格的影响，这些因素的共同作用决定了β系数的大小，其中，均值能很好地反映出数据整体的集中趋势，故选定平均价格和平均距离作为拟合价格的调整基数，得到定价拟合模型Ⅰ如下：

　　其中，P为APP内初步定价的平均值，dis为相对距离中全部数据的平均值，则有Pdis表示每一相对距离所对应的单位价格；dis实则为相对距离表中根据经纬度求出的与中心点间的实际距离；P为根据实际相对距离拟合得出的拟合价格。

　　由于式中的β系数是多种因素综合作用的结果，则可以根据数据的分布特征及相对比例，推断出β的值：根据可获得的全部数据量，以中心点为圆心，以一定比例的半径画出任务数据点的搜索圆形图，得出了三个搜索范围不同的划分区域。通过统计每个搜索区域的数据点的数量，得出了每个搜索区域与更大范围的搜索区域的数据点的比值趋于定值约为4/7，即β系数值为4/7。将已知数据带入模型(Ⅰ)进行检验，利用MATLAB基本拟合的工具箱，得到拟合价格与实际价格的残差，发现该拟合模型的残差均落于[-0.5，0.5]之间，可认为拟合精度较高，模型成立。

　　三、定价模型的优化

　　1.优化模型的建立

　　根据上述分析，参数β实质上只考虑了宏观上的区域经济因素，为了更好地优化模型，本文将会员对价格的整体影响定义为参数α，α指会员个体的微观因素对价格的综合影响，即卖方信息行为价格权重，经过分析，我们得到α的决定因素大体上涉及三个变量：

　　(1)会员地理位置与任务地理位置的相对比率，我们定义这个比率为地域相对值率AR，则有：

　　本文定义AR为地域相对值率，反映会员对于接单的意愿程度，按照公式(2)对AR计算，得到AR的平均值为0.25，而根据意愿程度高低进行区间划分，取AR=0.45作为会员愿意接单与否的基准值，进而从基础数据中筛选，统计得出符合条件的数据点的个数占总数据点个数的比重，即可得到AR的权重系数。

　　(2)任务分配时间(T)，预定的限额(lim M)，分配时实际上是根据预定限额所占比例进行配发的，则任务分配时与预定的任务限额中必然存在某种关系。因此，本文以6点为基准点，对6点半至7点半的时间点进行了转化，转化为与基准点的时间间隔，对时间间隔和预定的任务限额做散点图分析，发现两者的相关关系基本符合负一次方的幂函数分布，但是却又不是纯粹的幂函数分布，经过拟合验证得到：

　　其中，γ为某个固定的常数，反映出包含任务量抢单拥堵调整系数的整体权重。经测算，γ值为0.02%。

　　γ值的测定过程如下：

　　首先，由下列任务限额与任务劳累度的评判标准，选取任务完成难度较低的会员，这类会员由于任务难度均值在80%附近，几乎不可能产生违约风险，经统计该类会员共计1291人次，占总体人数的比值为0.69，即为任务限额对总体特征的影响权重。

　　其次，确定每天的抢单的黄金时间。据悉，每天早上的6点半到7点半是上班高峰期时间，则很多人无暇寻找自己所要的信息，同时，企业的运营同样需要及时的信息更新，以便为适应未来市场经营模式的变化做好准备，提前应对市场风险，这就为抢单拥堵提供了先决条件。因此，可以断定从早上6点半到7点半这个时间段，很有可能出现抢单拥堵，以及因为抢单拥堵从而造成价格走低，以及因有些会员抢不到任务订单有时间却做不了任务与有些会员抢到大量的任务订单却没时间做任务之间的总体效率低下的矛盾。

　　最后，根据时间段的标准化，可以统计处于6点半到7点半的数据量占总体数据量的比重，因此，将此黄金抢单时间段与总时间段的比值作为任务分配时间对价格的总体影响权重，进而推算出γ的估计值。γ值即反映出任务分配时间与分配限额的交互作用对总体价格调整的影响。

　　(3)会员的信誉度(CR)。暂不考虑优先权导致的抢单冲突，对信誉值进行如下信誉等级的划分：

　　针对第一个信誉区间对APP中的会员数据进行筛选，得到该区间的会员人数占总人数的1%，认为属于此类的会员信誉度优秀，很有可能完成任务，任务完成度为90%以上，故将此比例作为CR对总体价格影响权重系数。

　　由于上述三个变量之间是彼此独立的，因而我们可以将三个变量的影响进行叠加，进而确定微观因素对价格影响的权重。

　　根据上述分析建立模型Ⅱ：

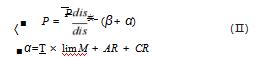
　　其中P为APP内初步定价的平均值，dis为相对距离中全部数据的平均值，则有P表示每一相对距离所对应的单位价格；dis实则为相对距离表中根据经纬度求出的与中心点间的实际距离；β为宏观区域因素，α为微观上信息卖方行为价格权重。P为根据实际相对距离拟合得出的拟合价格。针对得到的新模型代入数据，当模型(Ⅱ)所得到的价格与原始的数据价格之差处在(-1，1)，则开关变量0转换成1，即任务完成状况由未完成转化为完成。

　　2.优化模型的检验

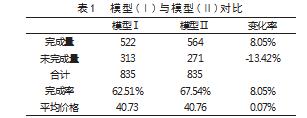
　　依据模型(Ⅱ)，代入数据检验发现，平均价格从40.73提高至40.76，改进以后不仅原先已经完成的任务完成了而且原本未完成的任务也显示完成。经过模型(Ⅱ)的优化，任务的完成量提高了8.05%，未完成的任务量降低了13.42%，平均制定的价格提高了0.07%。而模型(Ⅱ)与原方案对比可知，任务完成率提高了近80%。经定量定性分析可知，改进以后的任务完成率有显著的提高。因此，可以认为新的任务定价方案相较于原先APP的定价方案较为成功。

　　四、打包任务的定价模型

　　1.打包定价模型的建立

　　本文结合2.3中优化后的模型，探究打包的方式以及打包后新的定价模型。据悉打包模型的建立是基于买方市场的，而任务打包发布是为了将买方市场转化为平衡市场。任务打包以后必然会导致原先一对一的价格出现价格组合，那么价格组合一定不能拥有多个价格，故此，需要对价格组合重新制定均衡价格，使得打包组合中全部任务对应的总价满足供需双方的期望值。

　　依据已有文献，本文选定三个因素来反映造成买方市场原因：

　　其中，n1表示供给者提供的信息数量，n2表示需求者需要的信息数量，供给者期望价格水平为p1，需求者期望价格水平为p2，则在供求平衡时应当有n1p1=n2 p2，且当n1>n2时，有p1<p2。由此可知，价格减免比率会使得价格下降，即缓解市场的争抢，与价格的变动方向呈负相关关系。

　　其中，MTem为反映价格对任务量的促进影响，即买方信息出的价格超出平均价格所占实际价格的比值对当前成交量的影响。MTem与定价之间呈现正向相关关系。

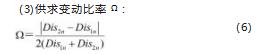
　　其中，Dis2n表示信息供应，Dis1n表示信息的需求；1/2为供求关系的变动周期。

　　由上述分析，可知价格减免比率与价格呈反向关系变动，MTem与供求变动比率均与价格呈现正向相关关系，且MTem与供求变动比率具有相同的波动性，可视同正向相关因素对价格共同增量调整的效应；而价格减免比率与价格呈现负相关关系。故基准价格如下：

　　当模型(Ⅲ)所得到的价格与原始的数据价格之差处在(-1，1)，则开关变量0转换成1，即任务完成状况由未完成转化为完成。

　　2.打包定价模型的检验

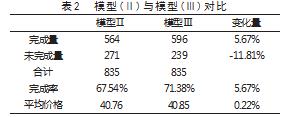
　　模型建立后，代入基础数据，得出平均定价由40.76变动至40.85，并依据价格筛选出前后定价方案中未完成的任务点，进行一一比对。对比发现，打包定价提高0.22%的同时，任务完成量增长了5.67%，未完成量降低11.81%。可见，任务打包后，价格虽有小幅度的提高，但并不影响任务完成率的提高，即将任务打包发布后，可在一定范围内调动会员的积极性，提高任务完成率。

　　五、结论

　　经模型仿真与检验，研究发现，当定价提高0.22%时，任务完成度增长5.67%。本项研究有助于类似自助劳务众包平台合理定价，实现平台利润最大化。

　　参考文献

　　[1]姜启源，谢金星.数学模型(第三版)[M].北京：高等教育出版社，2003.

　　[2]谭永基，蔡志杰.数学模型[M].上海：复旦大学出版社，2005.

　　[3]司守奎，孙兆亮.数学建模算法与应用[M].北京：国防工业出版社，2015.

　　[4]方方，王子英.K-means聚类分析在人体体型分类中的应用[J].东华大学学报(自然科学版)，2014，40(5)：593-598.

　　[5]王璐，朱家明，刘佩麟，等.基于Logistic回归青少年心理的风险评估及预警研究[J].齐齐哈尔大学学报(自然科学版)，2017，33(2)：77-83.